pytorch简单实例1---线性回归实例

在接触pytorch中CNN的全连接层，卷积层，池化层的创建后，我们便可以使用特定的梯度下降算法，以及特定的损失函数来做简单的线性回归了。

1.离散点的建立
因为是做线性回归，所以我们需要人为臆造一些符合某种线性关系的数据点

x_train = np.array([[.3], [1.2], [1.3], [2.], [3.2], [3.7], [4.], [4.9], [5.5], [6.], [6.7]], dtype=np.float32)
y_train = np.array([[.3], [1.], [2.1], [2.3], [3.], [2.9], [4.4], [5.], [5.5], [5.], [7.]], dtype=np.float32)
plt.figure()
plt.scatter(x_train, y_train)
plt.xlabel('x_train')
plt.ylabel('y_train')
plt.show()

2.创建线性回归的模型
就最常使用的方法是创建类属性，继承来自nn.Module的属性

# 线性模型y=w*x+b，w和b的权值（weight）需要在创建时候给定，x为输入，在调用的时候输入
class Linearmodel(nn.Module):

    def __init__(self, weight_w, weight_b):
        super(Linearmodel, self).__init__()

        self.model = nn.Sequential(
                                   nn.Linear(weight_w, weight_b),
                                   #CNN中的全连接层
                                   nn.Linear(weight_w, weight_b))
                                   #多创建一层，可以用于判断层数与损失值的关系
        # self.model = nn.Sequential(
        #     nn.Linear(1, 1),  # 创建一个线性层，
        #     nn.ReLU(inplace=True),
        # )  # 调用一个激活函数，由于在第一象限，激活函数意义不大，只为了更完整
        # 加上relu损失值更大

    def forward(self, x):
    #此部分尚未明确用意，但是参考许多文章，此函数不可省略
        out = self.model(x)
        return out

3.使用MSE损失和SGD的梯度优化方法来优化我们的模型

net = Linearmodel(weight_w, weight_b)  # 放入节点权值
criterion = nn.MSELoss()  # 指定损失函数,不能使用crossentropyloss，因为这里是1d
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)  # 指定梯度优化方式

for i in range(num_epochs):
    inputs = var(torch.from_numpy(x_train))
    targets = var(torch.from_numpy(y_train))  # 使用var可以将来自numpy变换后的tensor自动变成我们所需的数值

    optimizer.zero_grad()  # 梯度初始化
    outputs = net(inputs)  # 将输入值放入线性模型进行学习，得到输出结果
    loss = criterion(outputs, targets)  # 计算损失值，输出值与真实的目标值之间的差距
    loss.backward()  # 习惯将loss（损失值）的操作写在一起
    optimizer.step()  # 开始梯度优化
    # net.eval()  # 保留已经运算的输出结果
    if (i + 1) % 50 == 0:  # 便于查看计算过程
        print("训练步骤：【{}/{}】，loss={}".format(i + 1, num_epochs, loss.item()))

#训练结果
训练步骤：【50/1000】，loss=4.736996650695801
训练步骤：【100/1000】，loss=0.3275192975997925
训练步骤：【150/1000】，loss=0.3081437647342682
训练步骤：【200/1000】，loss=0.2996964454650879
训练步骤：【250/1000】，loss=0.2921964228153229
训练步骤：【300/1000】，loss=0.2855220139026642
训练步骤：【350/1000】，loss=0.27957385778427124
训练步骤：【400/1000】，loss=0.27426597476005554
训练步骤：【450/1000】，loss=0.2695239186286926
训练步骤：【500/1000】，loss=0.26528269052505493
训练步骤：【550/1000】，loss=0.26148539781570435
训练步骤：【600/1000】，loss=0.25808268785476685
训练步骤：【650/1000】，loss=0.2550306022167206
训练步骤：【700/1000】，loss=0.25229087471961975
训练步骤：【750/1000】，loss=0.2498299479484558
训练步骤：【800/1000】，loss=0.24761778116226196
训练步骤：【850/1000】，loss=0.2456279695034027
训练步骤：【900/1000】，loss=0.24383696913719177
训练步骤：【950/1000】，loss=0.24222415685653687
训练步骤：【1000/1000】，loss=0.24077099561691284

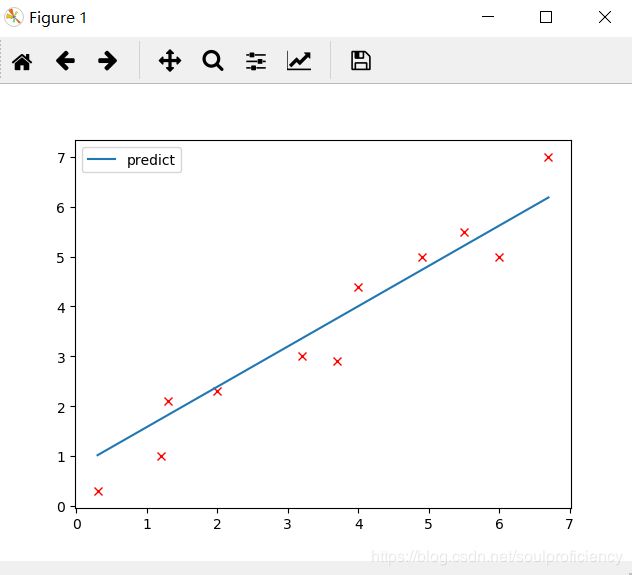
4.对于已经优化的模型我们作出回归线

predicted = net(var(torch.from_numpy(x_train))).data.numpy()#作出线性模型的图像所需的预测数据
plt.scatter(x_train, y_train)
#plt.plot(x_train, y_train, 'rx')
plt.plot(x_train, predicted, label='predict')
plt.legend()
plt.show()

结果图如下

完整代码如下

#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: 1234
@file: linear_practice.py
@time: 2020/06/27
@desc:
    格式化代码 ：Ctrl + Alt + L 
    运行代码 ： Ctrl + Shift + F10
    注释代码/取消注释 ： Ctrl + /
"""
import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
from torch.autograd import Variable as var

weight_w = 1
weight_b = 1  # 线性模型的权值
learning_rate = 0.001  # 学习率
num_epochs = 1000# 训练次数

x_train = np.array([[.3], [1.2], [1.3], [2.], [3.2], [3.7], [4.], [4.9], [5.5], [6.], [6.7]], dtype=np.float32)
y_train = np.array([[.3], [1.], [2.1], [2.3], [3.], [2.9], [4.4], [5.], [5.5], [5.], [7.]], dtype=np.float32)
plt.figure()
plt.scatter(x_train, y_train)
plt.xlabel('x_train')
plt.ylabel('y_train')
plt.show()


# 线性模型y=w*x+b，w和b的权值（weight）需要在创建时候给定，x为输入，在调用的时候输入
class Linearmodel(nn.Module):

    def __init__(self, weight_w, weight_b):
        super(Linearmodel, self).__init__()

        self.model = nn.Sequential(
                                   nn.Linear(weight_w, weight_b),#CNN中的全连接层
                                   nn.Linear(weight_w, weight_b))#多创建一层，可以用于判断层数与损失值的关系
        # self.model = nn.Sequential(
        #     nn.Linear(1, 1),  # 创建一个线性层，
        #     nn.ReLU(inplace=True),
        # )  # 调用一个激活函数，由于在第一象限，激活函数意义不大，只为了更完整
        # 加上relu损失值更大

    def forward(self, x):
        out = self.model(x)
        return out


net = Linearmodel(weight_w, weight_b)  # 放入节点权值
criterion = nn.MSELoss()  # 指定损失函数,不能使用crossentropyloss，因为这里是1d
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)  # 指定梯度优化方式

for i in range(num_epochs):
    inputs = var(torch.from_numpy(x_train))
    targets = var(torch.from_numpy(y_train))  # 使用var可以将来自numpy变换后的tensor自动变成我们所需的数值

    optimizer.zero_grad()  # 梯度初始化
    outputs = net(inputs)  # 将输入值放入线性模型进行学习，得到输出结果
    loss = criterion(outputs, targets)  # 计算损失值，输出值与真实的目标值之间的差距
    loss.backward()  # 习惯将loss（损失值）的操作写在一起
    optimizer.step()  # 开始梯度优化
    # net.eval()  # 保留已经运算的输出结果
    if (i + 1) % 50 == 0:  # 便于查看计算过程
        print("训练步骤：【{}/{}】，loss={}".format(i + 1, num_epochs, loss.item()))


predicted = net(var(torch.from_numpy(x_train))).data.numpy()#作出线性模型的图像所需的预测数据
plt.plot(x_train, y_train, 'rx')
plt.plot(x_train, predicted, label='predict')
plt.legend()
plt.show()