atcoder reguler contest 089 E graph xy

构造一个满足下列条件的有向图：
1. 顶点数不超过 300 300 ，其中有一个源点 S S 和一个汇点 T T
2. 没有重边和自环
3. 顶点由 1 1 至 N N 编号
4. 每条边的权值 ∈[0,100] ∈ [ 0 , 100 ] ，也可以是一个标签 X X 或 Y Y
5. 对于给定的每一对满足 x∈[1,A],y∈[1,B] x ∈ [ 1 , A ] , y ∈ [ 1 , B ] 的 (x,y) ( x , y ) ，在标签为 X X 的边的权值为 x x ，标签 Y Y 的权值为 y y 时，源点 S S 到汇点 T T 的最短路径长度为 d(x,y) d ( x , y )

1≤A,B≤10 1 ≤ A , B ≤ 10
1≤d(x,y)≤100 1 ≤ d ( x , y ) ≤ 100

---

每一条最短路都经过了一些 X X 边，一些 Y Y 边和一些常数边。我们发现如果有两条 S S 至 T T 的路径包含了相同多的 X X 边和 Y Y 边，常数边大的那条边是没有意义的，因为对于所有 (x,y) ( x , y ) ，常数项小的那条路径的权值肯定比常数项大的小。

且 d(i,j)≤100 d ( i , j ) ≤ 100 ，所以我们可以按如下方式构图：

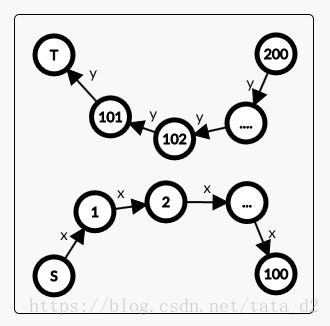
下半部分顶点可以自由向上半部分连常数权值的边。
我们设 f(i,j) f ( i , j ) 代表过了 i i 条 X X 边， j j 条 Y Y 边的常数边的权值，例如 f(1,2) f ( 1 , 2 ) 就代表了图中 1 1 号点与 102 102 号点之间常数边的权值。

那么，

d(i,j)=min{ f(a,b)+ai+bj } d ( i , j ) = m i n {   f ( a , b ) + a i + b j   }

因为我们要确定 f(a,b) f ( a , b ) 的值，所以我们反过来考虑

f(a,b)≤d(i,j)−ai−bj,  i≤A,j≤B f ( a , b ) ≤ d ( i , j ) − a i − b j ,     i ≤ A , j ≤ B

我们让每一个 f(a,b) f ( a , b ) 都尽量小，这样就给最小的 d(i,j) d ( i , j ) 提供了一条最短路。

确定每个 f(a,b) f ( a , b ) 的值后，我们只需要验证一下是否符合即可。

O(d(i,j)2AB) O ( d ( i , j ) 2 A B )

code：

    #include 
    using namespace std;
    const int N = 350;
    const int INF = 1<<30;

    int a, b, s, t, sum, d[N][N], f[N][N];

    inline void ck_min( int &a, int b ) { if( a > b ) a = b; }
    inline void ck_max( int &a, int b ) { if( a < b ) a = b; }

    inline bool check( int x, int y, int val )
    {
        int res = INF;
        for( int i = 0; i <= 100; i ++ )
            for( int j = 0; j <= 100; j ++ )
                if( f[i][j] >= 0 ) ck_min( res, i*x + j*y + f[i][j] );

    //  printf( "x:%d, y:%d, res:%d\n", x, y, res );
        return res == val;
    }

    int main()
    {
        memset( f, -1, sizeof( f ) );

        scanf( "%d%d", &a, &b );
        for( int i = 1; i <= a; i ++ )
            for( int j = 1; j <= b; j ++ )
                scanf( "%d", &d[i][j] );

        s = 201, t = 202; 
        // s --> 1 --> 2 --> ... --> 100
        // t <-- 101 <-- 102 <-- ... <-- 200

        for( int i = 0; i <= 100; i ++ )
            for( int j = 0; j <= 100; j ++ )
            {
                int tmp = -INF;
                for( int _a = 1; _a <= a; _a ++ )
                    for( int _b = 1; _b <= b; _b ++ )
                        ck_max( tmp, d[_a][_b] - i*_a - j*_b ); 
                f[i][j] = tmp; 
                if( f[i][j] < 0 ) break;

                sum ++;
    //          printf( "i:%d, j:%d, f:%d\n", i, j, f[i][j] );
            }

        for( int i = 1; i <= a; i ++ )
            for( int j = 1; j <= b; j ++ )  
                if( !check( i, j, d[i][j] ) ) {
                    printf( "Impossible\n" ); return 0;
                } 

        printf( "Possible\n" );

        printf( "%d %d\n", 202, sum+200 );
        for( int i = 1; i < 100; i ++ )
            printf( "%d %d X\n%d %d Y\n", i, i+1, i+101, i+100 );

        printf( "%d %d X\n%d %d Y\n", s, 1, 101, t );
        for( int i = 0; i <= 100; i ++ )
            for( int j = 0; j <= 100; j ++ )
                if( f[i][j] >= 0 )  printf( "%d %d %d\n", !i ? s : i, !j ? t : j+100, f[i][j] );

        printf( "%d %d\n", s, t );

        return 0;
    }