数据挖掘十大算法（九）：朴素贝叶斯原理、实例与Python实现

一、条件概率的定义与贝叶斯公式

二、朴素贝叶斯分类算法

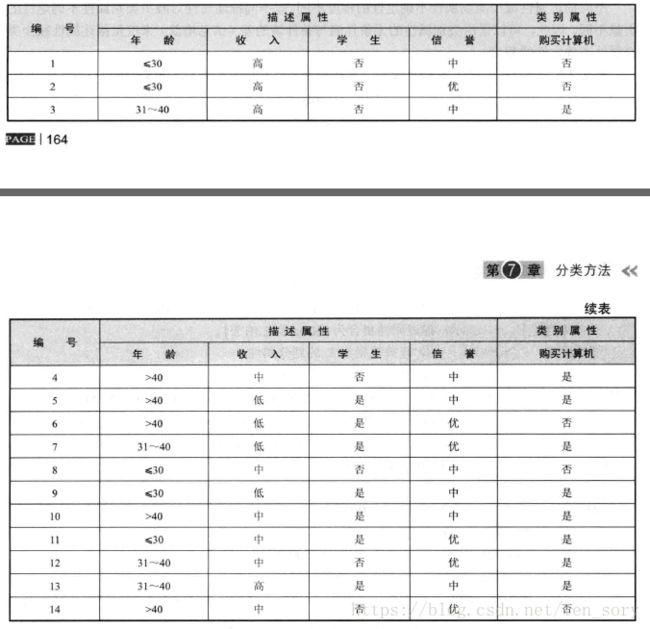
朴素贝叶斯是一种有监督的分类算法，可以进行二分类，或者多分类。一个数据集实例如下图所示：

现在有一个新的样本， X = (年龄：<=30, 收入：中， 是否学生：是， 信誉：中)，目标是利用朴素贝叶斯分类来进行分类。假设类别为C(c1=是 或 c2=否)，那么我们的目标是求出P(c1|X)和P(c2|X)，比较谁更大，那么就将X分为某个类。

下面，公式化朴素贝叶斯的分类过程。

三、实例

下面，将下面这个数据集作为训练集，对新的样本X = (年龄：<=30, 收入：中， 是否学生：是， 信誉：中)  作为测试样本，进行分类。

我们可以将这个实例中的描述属性和类别属性，与公式对应起来，然后计算。

 

四、Python实现

现在，利用Python编写上述实例对应的代码，代码如下。

# 针对 “买电脑”实例进行朴素贝叶斯分类


if __name__ == '__main__':

    # 描述属性分别用数字替换
    # 年龄, <=30-->0, 31~40-->1, >40-->2
    # 收入, '低'-->0, '中'-->1, '高'-->2
    # 是否学生, '是'-->0, '否'-->1
    # 信誉: '中'-->0, '优'-->1
    # 类别属性用数字替换
    # 购买电脑是-->0, 不购买电脑否-->1
    MAP = [{'<=30': 0, '31~40': 1, '>40': 2},
           {'低': 0, '中': 1, '高': 2},
           {'是': 0, '否': 1},
           {'中': 0, '优': 1},
           {'是': 0, '否': 1}]

    # 训练样本
    train_samples = ["<=30 高 否 中 否",
                     "<=30 高 否 优 否",
                     "31~40 高 否 中 是",
                     ">40 中 否 中 是",
                     ">40 低 是 中 是",
                     ">40 低 是 优 否",
                     "31~40 低 是 优 是",
                     "<=30 中 否 中 否",
                     "<=30 低 是 中 是",
                     ">40 中 是 中 是",
                     "<=30 中 是 优 是",
                     "31~40 中 否 优 是",
                     "31~40 高 是 中 是",
                     ">40 中 否 优 否"]

    # 下面步骤将文字，转化为对应数字
    train_samples = [sample.split(' ') for sample in train_samples]
    # print(train_samples)
    # exit()
    train_samples = [[MAP[i][attr] for i, attr in enumerate(sample)]for sample in train_samples]
    # print(train_samples)

    # 待分类样本
    X = '<=30 中 是 中'
    X = [MAP[i][attr] for i, attr in enumerate(X.split(' '))]

    # 训练样本数量
    n_sample = len(train_samples)

    # 单个样本的维度： 描述属性和类别属性个数
    dim_sample = len(train_samples[0])

    # 计算每个属性有哪些取值
    attr = []
    for i in range(0, dim_sample):
        attr.append([])

    for sample in train_samples:
        for i in range(0, dim_sample):
            if sample[i] not in attr[i]:
                attr[i].append(sample[i])

    # 每个属性取值的个数
    n_attr = [len(attr) for attr in attr]

    # 记录不同类别的样本个数
    n_c = []
    for i in range(0, n_attr[dim_sample-1]):
        n_c.append(0)

    # 计算不同类别的样本个数
    for sample in train_samples:
        n_c[sample[dim_sample-1]] += 1

    # 计算不同类别样本所占概率
    p_c = [n_cx / sum(n_c) for n_cx in n_c]
    # print(p_c)

    # 将用户按照类别分类
    samples_at_c = {}
    for c in attr[dim_sample-1]:
        samples_at_c[c] = []
    for sample in train_samples:
        samples_at_c[sample[dim_sample-1]].append(sample)

    # 记录 每个类别的训练样本中，取待分类样本的某个属性值的样本个数
    n_attr_X = {}
    for c in attr[dim_sample-1]:
        n_attr_X[c] = []
        for j in range(0, dim_sample-1):
            n_attr_X[c].append(0)

    # 计算 每个类别的训练样本中，取待分类样本的某个属性值的样本个数
    for c, samples_at_cx in zip(samples_at_c.keys(), samples_at_c.values()):
        for sample in samples_at_cx:
            for i in range(0, dim_sample-1):
                if X[i] == sample[i]:
                    n_attr_X[c][i] += 1

    # 字典转化为list
    n_attr_X = list(n_attr_X.values())
    # print(n_attr_X)

    # 存储最终的概率
    result_p = []
    for i in range(0, n_attr[dim_sample-1]):
        result_p.append(p_c[i])

    # 计算概率
    for i in range(0, n_attr[dim_sample-1]):
        n_attr_X[i] = [x/n_c[i] for x in n_attr_X[i]]
        for x in n_attr_X[i]:
            result_p[i] *= x

    print('概率分别为', result_p)

    # 找到概率最大对应的那个类别，就是预测样本的分类情况
    predict_class = result_p.index(max(result_p))
    print(predict_class)

运行结果如图所示：

表明，样本被分为第一类，即会购买电脑。对应的概率与手动计算的结果相同。

 

参考：

1. 数据挖掘十大算法

2. 数据仓库与数据挖掘 李春葆

更新

有在评论中说到这个结果：

 [0.0011757789535567313, 0.16457142857142862] 

我运行了多次原来的代码，但是结果始终如一。最后，又仔细阅读了一遍代码，发现问题在“n_attr_X”这个变量在转化为list的过程。

n_attr_X={0: [2, 4, 6, 6], 1: [3, 2, 1, 2]}为一个字典，如果转化为list则是[[3, 2, 1, 2], [2, 4, 6, 6]]，这样可以得到我的结果。

但是如果，n_attr_X={1: [3, 2, 1, 2], 0: [2, 4, 6, 6]}，那么转化为list之后就是[[3, 2, 1, 2], [2, 4, 6, 6]]。这样默认是类别为0的各个属性个数为3，2，1，2，因为后面使用的是列表，默认下标就代表着类别标签。可以在这个转化步骤之后，加上这句代码：

n_attr_X[0], n_attr_X[1] = n_attr_X[1], n_attr_X[0]

结果就不一样了。

所以最好用有序字典，并且不要采用“下标就代表着类别标签”的方法。