机器学习之多项式拟合

实验内容

目标

掌握最小二乘法求解（无惩罚项的损失函数）、掌握加惩罚项（2范数）的损失函数优化、梯度下降法、共轭梯度法、理解过拟合、克服过拟合的方法(如加惩罚项、增加样本)

要求

1. 生成数据，加入噪声；
2. 用高阶多项式函数拟合曲线；
3. 用解析解求解两种loss的最优解（无正则项和有正则项）
4. 优化方法求解最优解（梯度下降，共轭梯度）；
5. 用你得到的实验数据，解释过拟合。
6. 用不同数据量，不同超参数，不同的多项式阶数，比较实验效果。
7. 语言不限，可以用matlab，python。求解解析解时可以利用现成的矩阵求逆。梯度下降，共轭梯度要求自己求梯度，迭代优化自己写。不许用现成的平台，例如pytorch，tensorflow的自动微分工具。

实验步骤

生成随机数据

sin(2πx) 加入高斯噪声

def generateData(x1, x2, noise, n):
    mu, sigma = 0, 0.1
    while True:
        s = np.random.normal(mu, sigma, n)
        if (abs(mu-np.mean(s)) < 0.01) & (abs(sigma - np.std(s, ddof=1)) < noise):
            break
    x = np.linspace(x1, x2, n)
    y = np.sin(2.0*math.pi*x) + s * noise
    return x, y

高阶多项式拟合

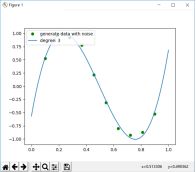
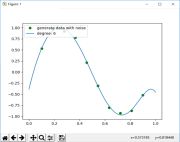
从0阶到10阶，调用polyfit函数进行拟合并绘图

trainSet = generateData(0.1, 0.9, 0.5, 10)
for degree in range(10):
    coff = polyfit(trainSet[0], trainSet[1], degree)
    my_plot = np.polyval(coff, x_plot)
    plt.plot(trainSet[0], trainSet[1], color='g', linestyle='', marker='o', label=u"generate data with noise")
    plt.plot(x_plot, my_plot, linestyle='-', marker='', label="degree: " + str(degree))
    plt.legend(loc='upper left')
    plt.show()

无正则项的解析解

推导过程网上有很多，比如这个.
首先构造矩阵，因为系数从高阶到低阶，所以矩阵要从左到右的降阶数构造，然后直接套公式即可。

X0 = np.zeros((10, 10))
for k0 in range(10):
    for n0 in range(10):
        n0 = 9 - n0
        if (n0 == 9):
            X0[k0][n0] = 1
        else:
            X0[k0][n0] = X0[k0][n0 + 1] * trainSet[0][k0]

a1 = X0
a2 = np.transpose(a1)
Ans = np.dot(np.dot(np.linalg.inv(np.dot(a2, a1)), a2), np.transpose(trainSet[1]))

有正则项的解析解

直接加入正则项即可。e^-18 效果最好，可调整参数看效果

lam = np.exp(-18)
Ans = np.dot(np.dot(np.linalg.inv(np.dot(a2, a1) + lam * np.eye(10)), a2), np.transpose(trainSet[1]))

梯度下降法

关于原理，参见这里,或者这里.
当然有能力最好维基百科，全面清晰。

网上很多包括csdn上都有很多代码分享，但确实很多都有问题，老师也不推荐csdn上。之前搜索学习的时候参考的几份代码也都是有问题的，搞学术这种东西还是不能马虎，自己系统学习比照葫芦画瓢不明所以还是要好很多的。

def loss_function(theta, X):
    P = np.mat(trainSet[1])
    diff = np.dot(X, theta) - np.transpose(P)
    return 0.5 / 10 * np.dot(np.transpose(diff), diff) + lam * np.dot(np.transpose(theta), theta)


def gradient_function(theta):
    P = np.mat(trainSet[1])
    diff = np.dot(X, theta) - np.transpose(P)
    return 1.0 / 10 * np.dot(np.transpose(X), diff) + lam * theta


def gradient_descent(lr):
    theta = np.ones((10, 1))
    gradient = gradient_function(theta)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - lr * gradient
        gradient = gradient_function(theta)
    return theta

X = np.zeros((10, 10))
for k0 in range(10):
    for n0 in range(10):
        if (n0 == 0):
            X[k0][n0] = 1
        else:
            X[k0][n0] = X[k0][n0 - 1] * trainSet[0][k0]
            
lr = 0.01
optimal = gradient_descent(lr)
print('optimal:', optimal)
print('error function:', loss_function(optimal, X)[0, 0])

共轭梯度法

强推维基百科的条目。
原理基本就是线性代数那一套，推导还有示例还是很容易明白的。

代码基本初始化之后套进去就ok。

while True:
    alphak = np.dot(np.transpose(r[k]), r[k]) / np.dot(np.dot(np.transpose(p[k]), A), p[k])
    x[k + 1] = x[k] + alphak * p[k]
    r[k + 1] = r[k] - alphak * np.dot(A, p[k])
    if (np.all(np.absolute(r[k + 1]) < 1e-5)):
        break
    beita = np.dot(np.transpose(r[k + 1]), r[k + 1]) / np.dot(np.transpose(r[k]), r[k])
    p[k + 1] = r[k + 1] + beita * p[k]
    k = k + 1

然后就是对比两种梯度法的优劣了，网上有很多。