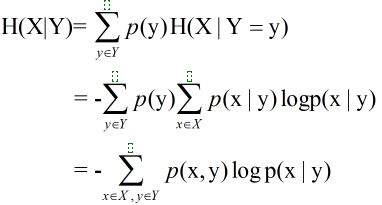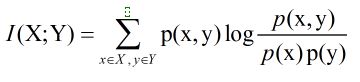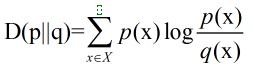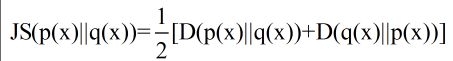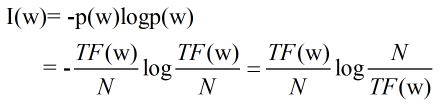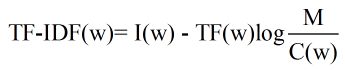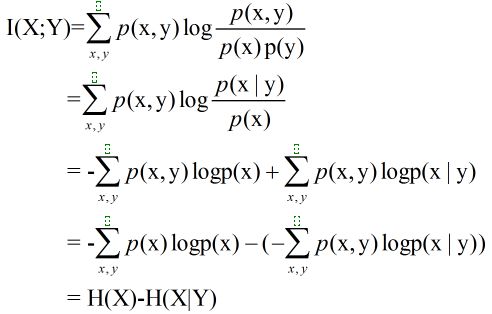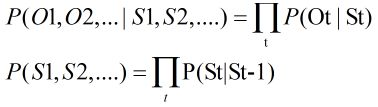16年一月份阅读了吴军的《数学之美》,真有种相见恨晚的感觉!对于刚刚学习自然语言处理的人来说,这是最佳入门读物,没有之一。下面是我在学习中做的一些知识点的阅读笔记,有些内容、公式摘自Tomas M.Cover的《信息论基础》,详情请参考原著,本文仅作个人阅读笔记学习使用。
1.熵、联合熵、条件熵、互信息、相对熵
信息的作用是排除不确定性,信息量就得关于不确定性的多少。
对于任意一个随机变量X,其熵为:
对于服从联合分布为p(x,y)的一对离散随机变量,即x,y一起出现的概率,其联合熵为
条件熵即在知道Y取不同值时X的概率分布,在Y的条件下的条件熵为
延伸:一对随机变量的联合熵等于其中一个随机变量的熵加上另一个随机变量的条件熵:
互信息(Mutual Information)度量两个随机事件的相关性,度量一个随机变量包含另一个随机变量的信息量,即在给定另一随机变量知识的条件下,原随机变量不确定度的缩减量:
相对熵(Relative Entropy),又叫交叉熵,也用来衡量相关性,但衡量的是两个取值为正的函数的相关性,刻画两个概率分布之间的距离的一种度量,互信息是它的特殊形式。相对熵D(p||q)度量当真实分布为p而假设分布为q时的无效性。两个概率密度函数为p(x)和q(x)之间的相对熵公式如下:
延伸:两个随机变量X和Y,他们的联合概率密度函数为p(x,y),其边际概率密度函数分别是p(x)和
p(y)
。互信息为
联合分布
p(x,y)和
乘积分布
p(x)p(y)之间的相对熵:
相对熵是不对称的,即
为了使用的方便性,詹森和香农提出新的相对熵计算方法,即将上面的不等式两边取平均:
这一计算方法曾用在google的自动问答系统中,衡量两个答案的相似性。如何衡量需要进一步探索!
相对熵的应用:文中提出利用相对熵可以得到词频率-逆向文档频率(TF-IDF)。IDF的公式为log(D/Dw),其中D是全部文档数,Dw是关键词w出现的文档数量。就是一个特定条件下(TF为特定条件)关键词的概率分布的相对熵。
推导思路:一个关键词的权重可以利用这个词的信息量来衡量,即:
其中N是整个语料库的大小,是个可以忽略的常数。上述公式可以简化为:
考虑关键词的分辨率,满足一下假设:
(1)每个文献大小基本相同,均为M个词,M=N/D;
(2)一个关键词无论在文献中出现几次,贡献都相同,其要么在一个文献中出现C(w)=TF(w)/D(w)次,要么出现零次。
此时每个关键词的权重及其信息量表示为:
可以看出关键词的信息量I(w)越大,TF-IDF值越大;C(w)即关键词命中的文献中关键词平均出现的次数越多,即第二项越小,TF-IDF值越大。
熵与互信息的关系:
由此可知,互信息I(X,Y)是在给定Y知识的条件下X的不确定度的缩减量,也可得到 I(X;Y)=H(Y)-H(Y|X) ,即X含有Y的信息量和Y含有X的信息量等同。
由联合熵的分解公式 H(X,Y)=H(X)+H(Y|X) 、互信息的分解公式 I(X;Y)=H(Y)-H(Y|X),可得
I(X;Y)=H(X)+H(Y)-H(X,Y)。
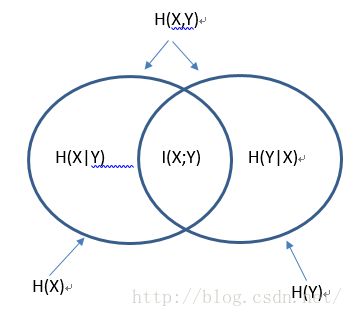
扩展:H(X)、H(Y)、H(X,Y)、H(X|Y)、H(Y|X)、I(X;Y)之间的关系用文氏图表示如下:
2.最大熵原理(The Maximum Entropy Principle)
最大熵原理指出,对一个随机事件的概率分布进行预测时,应该满足全部已知的条件而对未知的情况不做任何主观假设。在这种情况下,概率分布最均匀,预测的风险最小。因为此时概率分布的信息熵最大,所以称这种模型为“最大熵模型”!通俗理解就是当我们遇到不确定性时,就要保留各种可能性。
匈牙利著名数学家、信息论最高奖香农奖得主希萨(I.Csiszar)证明:对任何一组不自相矛盾的信息,最大熵模型不仅存在而且是唯一的。并且都有同一个非常简单的形式--指数函数。最大熵模型计算量很大,宾夕法尼亚大学马库斯教授的高徒拉纳帕提(Adwait Ratnaparkhi)找到几个最适合用最大熵模型且计算量相对不太大的自然语言处理问题,比如词性标注、句法分析。他成功将上下文信息、词性(名词、动词、形容词)以及主谓宾等句子成分,通过最大熵模型结合起来,做出当时世界上最好的词性标注系统和句法分析器。
模型的训练:如下图通过20种特征计算网页d的概率的最大熵模型

![]()
其中归一化因子Z保证概率加起来等于1,参数λ需要通过模型训练获得。
最原始的最大熵模型训练方法为通用迭代算法GIS(Generalized Iterative Scaling),其原理大致为:
(1)假定第零次迭代的初始模型为等概率的均匀分布
(2)用第N次迭代的模型来估算每种信息特征在训练数据中的分布,如果超过了实际的,就把相应的模型参数变小,否则变大
(3)重复步骤2 直到收敛
这种训练方法为典型的期望值最大化算法(Expectation Maximization,简称EM),由希萨解释清楚这种算法的物理含义。由于GIS算法每次迭代时间很长,需要迭代很多次才收敛,且不太稳定,因此很少实际使用,只通过其来了解最大熵模型的算法。之后达拉.皮垂兄弟对其改进,提出了改进迭代算法IIS(Improved Iterative Scaling),使最大熵模型训练时间缩短一两个数量级,吴军在约翰.霍普金斯大学读博士时发现一种数学变换,又将训练时间在IIS基础上减少两个数量级。
总结:最大熵模型形式简单,从效果上看是唯一一种既能满足各种信息源的限制条件又能保证平滑性的模型,但实现复杂,计算量巨大。
扩展阅读:
EM算法的物理含义
3.贝叶斯网络
由于网络中,每个节点的概率都可以用贝叶斯公式来计算,因此得名贝叶斯网络。马尔科夫假设保证了贝叶斯网络便于计算,即网络中的每个状态取决于前面有限个状态,但贝叶斯网络的拓扑结构比马尔可夫链灵活,不受其链状结构的约束。即马尔科夫链是贝叶斯网络的特例,而贝叶斯网络是马尔科夫链的推广。贝叶斯网络是一个加权的有向图。
应用:吴军说利用贝叶斯网络找出近义词和相关词,但对于具体如何应用还需探索;
文中举例贝叶斯网络在词分类中的应用,即针对文章、概念(主题)、关键词之间建立贝叶斯网络,感觉和LDA(Latent Dirchlet Allocation)比较相似。实现的难点在于如何从大规模文章中准确自动抽取关键词,通过句法分析是否能够解决?这又涉及到中文分词和中文句法解析器的准确性问题。其次无论是通过文本、关键字关联矩阵的奇异值分解还是使用余弦举例的聚类,词语分出来的每一类为一个概念,这个概念是如何标记的?是按照顺序标记还是人工判定为一个具体的主题?
书中指出只考虑关键词和文本的关系,较少考虑关键词的上下文关系使得概念的聚类过于广泛,无法应用。google之后对这个网络的重构中考虑关键词的相似性从原来的在文本中同现扩展为上下文中同现,同时支持不同颗粒的概念。其意思是否是对每一个词语又根据其在文章中的上下文不同细分为结合上下文的下位类?这样原先的词语维度就会扩展为原先的好多倍。不同颗粒的概念是否和上下文选择的个数有关?
贝叶斯网络的训练:分为结构和参数的训练两个部分。(1)结构的训练,优化的贝叶斯结构要保证其产生的序列可能性最大即后验概率最大。理论上需要考虑每一天路径,计算复杂度无法实现。一般采用贪心算法(Greedy Algorithm)即在每一步方向寻找有限步,缺点是会陷入局部最优,最终远离全局最优解。可以采用蒙特卡洛(Monte Carlo)的方法,找许多随机数在贝叶斯网络中检测是否陷入局部最优,但其计算量较大。还有一个新方法是计算网络中节点之间两两的互信息,保留互信息较大的节点直接的链接,然后对简化的网络进行完备的搜索,找到全局优化的结构。(2)参数的训练即计算网络中节点之间弧的权重,利用期望值最大化算法EM。
扩展阅读:数学之美番外篇:平凡而又神奇的贝叶斯网络(强烈建议多读几遍!!!)
奥卡姆剃刀的精神:如果两个理论具有相似的解释力度,那么优先选择那个更简单的(往往也正是更平凡的,更少繁复的,更常见的)。最大似然方法:在贝叶斯模型比较中,不考虑先验概率的方法就是最大似然方法。
公式P(h | D) ∝ P(h) * P(D | h)中h表示预测可能的值,D表示观测数据。这个式子的抽象含义是:对于给定观测数据,一个猜测是好是坏,取决于“这个猜测本身独立的可能性大小(先验概率,Prior )”即P(h)和“这个猜测生成我们观测到的数据的可能性大小”(似然,Likelihood )即P(D | h)的乘积。奥卡姆剃刀就是说 P(h) 较大的模型有较大的优势,而最大似然则是说最符合观测数据的(即 P(D | h) 最大的)最有优势。另外工作在贝叶斯公式的似然P(D | h)上的剃刀叫做贝叶斯奥卡姆剃刀(Bayesian Occam’s Razor),即似然估计也选择了最简单的模型。
最优贝叶斯推理的思想是就是将多个模型对于未知数据的预测结论加权平均起来(权值就是模型相应的概率),但模型空间可能是连续的,计算非常耗时。感觉和随机森林算法有相似之处!
朴素贝叶斯就是指贝叶斯方法加上了条件独立假设。
层次贝叶斯模型,前面讲的贝叶斯,都是在同一个事物层次上的各个因素之间进行统计推理,然而层次贝叶斯模型在哲学上更深入了一层,将这些因素背后的因素(原因的原因,原因的原因,以此类推)囊括进来。一个教科书例子是:如果你手头有 N 枚硬币,它们是同一个工厂铸出来的,你把每一枚硬币掷出一个结果,然后基于这 N 个结果对这 N 个硬币的 θ (出现正面的比例)进行推理。如果根据最大似然,每个硬币的 θ 不是 1 就是 0 (这个前面提到过的),然而我们又知道每个硬币的 p(θ) 是有一个先验概率的,也许是一个 beta 分布。也就是说,每个硬币的实际投掷结果 Xi 服从以 θ 为中心的正态分布,而 θ 又服从另一个以 Ψ 为中心的 beta 分布。层层因果关系就体现出来了。进而 Ψ 还可能依赖于因果链上更上层的因素,以此类推。这和LDA的核心思想很相似。
LDA漫游指南,LDA算法是英国剑桥大学的David M.Blei以PLSA(LDA之前的另一个概率模型)为基础,加上了贝叶斯先验,从而诞生了LDA算法。
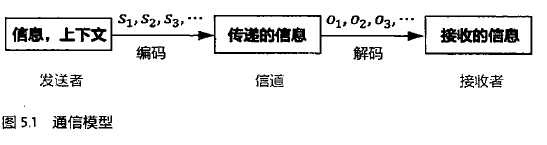
4.通信模型、马尔可夫链、隐马尔可夫模型、条件随机场
问题:根据接收到的观测信号O1,O2,...如何推测信号源发出的信息S1,S2,.....
数学表示:S1,S2,.....=Arg Max P(S1,S2,.....|O1,O2,...)
=P(O1,O2,...|S1,S2,....)P(S1,S2,....) / P(O1,O2,..)
P(O1,O2,..)已经观测到,可以忽略掉。
19世纪概率论从对随机变量的研究发展到对随机变量的时间序列即随机过程的研究。马尔可夫提出的马尔可夫假设为随机过程中各个状态St的概率分布,只与它的前一个状态S(t-1)有关,即P(St|S1,S2,S3,...St-1)=P(St|St-1)。
符合这一假设的过程为马尔可夫过程,即马尔可夫链。
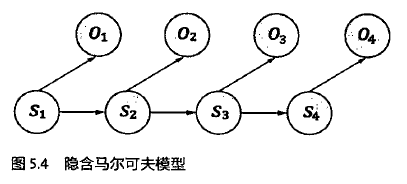
隐含马尔可夫模型满足两个条件:(1)有一个隐含的满足马尔可夫链的状态序列S1,S2,.....,观测不到
(2)但是这个隐藏的序列在每个时刻t都会输出一个符号Ot,且Ot跟St相关且仅跟St相关。即St和Ot满足独立输出假设。
第一个问题可以简化表示为
隐含马尔科夫模型的训练:
(1)给定一个模型,如何计算某个特定的输出序列的概率;(Forward-Backward算法)
(2)给定一个模型和某个特定的输出序列,如何找到最可能产生这个输出的状态序列;(维特比算法)
(3)给定足够的观测数据,如何估计隐含马尔科夫模型的参数。
模型参数有:转移概率,即前一个状态St-1到当前状态St的概率P(St|St-1);
生成概率,即每个状态St产生输出符号Ot的概率P(Ot|St
)。
模型参数的训练有两种方法:一种是利用大量人工标注的数据,称为有监督的训练方法;一种是仅通过大量观测到的信号O1,O2,...就能推测出模型参数,称为无监督的训练方法,其中主要使用的是鲍姆-韦尔奇算法(Baum-Welch Algorithm)即使用期望值最大化算法EM通过迭代不断估计新的模型参数,使得目标函数达到最大化。
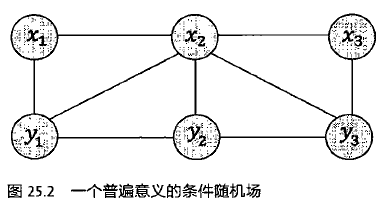
互联网时代,网民生成的句子很随意,利用拉纳帕提的括括号的深层文法分析得出全部的语法树,分析出的正确率很低。好在很多自然语言处理的应用中只要做浅层分析(Shallow Parsing)也叫部分句法分析(partial parsing)或语块分析(chunk parsing),即不需要得出全部的语法树,只需要找出其中主要的词组和他们之间的关系即可。条件随机场(Conditional Random fields)简称CRF,使得句子浅层分析的正确率达到95%。
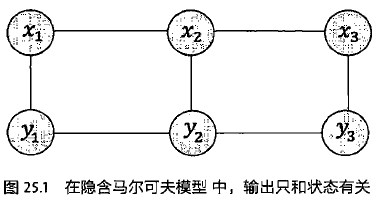
条件随机场也是隐含马尔科夫模型的一种扩展,和贝叶斯网络一样也是一种概率图模型,但贝叶斯网络是有向图,条件随机场是无向图。解释如下。
隐马模型中,观测值xi只取决于产生它的状态yi,和前后状态yi-1,yi+1都无关,而条件随机场则把xi,yi-1,yi,yi+1都考虑进来。
扩展阅读:条件随机场技术博客,其中介绍了模型的训练算法和一些c++实现工具;
条件随机场文献阅读指南,详细介绍了相关文献。
5.动态规划、维特比算法
动态规划(Dynamic Programming)通俗讲就是把一个复杂的问题拆分为一系列简单的问题(状态)和状态转移公式,以递推的方式来解决。
其他解释详见: 知乎中关于动态规划的讨论
。利用动态规划可以解决任何一个图中的最短路径问题。
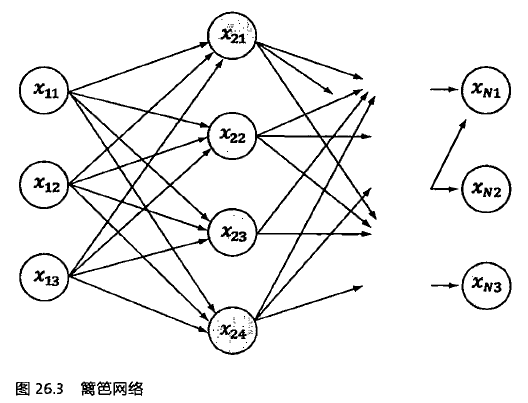
维特比算法是应用最广的特殊的动态规划算法,是针对篱笆网络(Lattice)的有向图最短路径问题提出的。
即隐马尔可夫模型中的隐含序列状态是固定的,但是每个状态值是可变的,就形成上图的篱笆网络。其中Xij表示状态Xi的第j个可能的值,每个状态Xi的输出是固定的yi。原先的转移概率P(Xi|Xi-1)变为更复杂的篱笆网络。维特比算法的基础可以概括为三点:
(1)如果概率最大的路径P经过某个点如X22,那么从起点S到X22的子路径Q一定是S到X22之间的最短路径;
(2)从起点S到重点E的路径必定经过第i时刻的某个状态,假定第i时刻有k个节点,那么如果记录了从S到第i个状态的所有k个节点的最短路径,最终的最短路径必定经过其中的一条。那么在任何某个时刻,只要考虑非常有限条候选路径即可。
(3)结合上述两点,当从状态i进入状态i+1时,假设从S到状态i上各个节点的最短路径已经找到,并且记录在这些节点上,那么在计算从S到i+1状态的某个节点的最短路径时,只要考虑从S到i的所有的k个节点的最短路径,以及从这k个节点到i+1状态的节点的距离即可。
6.期望最大化算法(Expectation Maximization Algorithm)
一般性问题描述:根据许多观测数据,让计算机不断迭代来学习一个模型。首先,根据现有模型(比如均匀分布)计算各个观测数据输入到模型的计算结果,这个过程就叫做期望值计算过程(Expectation)即E过程;接着重新计算模型参数,使期望值最大化,这个过程就是最大化过程(Maximization)即M过程。
EM算法的应用举例:
(1)前面提到的隐马尔可夫模型的训练方法鲍姆-韦尔奇算法(Baum-Welch Algorithm)就是EM算法,其中E过程就是根据现有的模型计算每个状态之间转移的次数以及每个状态产生他们输出的次数,M过程就是根据这些次数重新估计隐马模型的参数。他的最大化的目标函数就是观测值的概率。
(2)最大熵模型参数训练的通用迭代算法也是EM算法,E过程是根据现有的模型计算每一个特征的数学期望值,M过程就是根据这些特征的数学期望值和实际观测值的比值,调整模型参数,最大化的目标函数就是熵函数。
注意:EM算法得到的解不一定是全局最优解而可能是局部最优解。如果优化的目标函数是凸函数,那么得到的一定是全局最优解。