数据结构一线性表 (顺序表、单链表、双链表)
版权声明:本文为openXu原创文章【openXu的博客】,未经博主允许不得以任何形式转载
文章目录
- 1、线性表及其逻辑结构
- 1.1 线性表的定义
- 1.2 线性表的抽象数据类型描述
- 2、线性表的顺序存储结构
- 2.1 顺序表
- 2.2 顺序表基本运算的实现
- 算法分析:
- 3、线性表的链式存储结构
- 3.1 链表
- 3.2 单链表基本运算的实现
- 算法分析
- 3.3 双链表
- 双链表基本运算的实现
- 算法分析
- 3.4 循环链表
- 4、有序表
- 源码下载
1、线性表及其逻辑结构
线性表是最简单也是最常用的一种数据结构。英文字母表(A、B、…、Z)是一个线性表,表中每个英文字母是一个数据元素;成绩单是一个线性表,表中每一行是一个数据元素,每个数据元素又由学号、姓名、成绩等数据项组成。
1.1 线性表的定义
线性表是具有相同特性的数据元素的一个有限序列。线性表一般表示为:
L = (a1, a2, …, ai,ai+1 ,…, an)
线性表中元素在位置上是有序的,这种位置上有序性就是一种线性关系,用二元组表示:
L = (D, R)
D = {ai| 1≤i≤n, n≥0}
R = {r}
r = { | 1≤i≤n-1}
1.2 线性表的抽象数据类型描述
将线性表数据结构抽象成为一种数据类型,这个数据类型中包含数据元素、元素之间的关系、操作元素的基本算法。对于基本数据类型(int、float、boolean等等)java已经帮我们实现了用于操作他们的基本运算,我们需要基于这些基本运算,为我们封装的自定义数据类型提供操作它们的算法。比如数组就是一种被抽象出来的线性表数据类型,数组自带很多基本方法用于操作数据元素。
Java中的List我们经常会使用到,但是很少关注其内部实现,List是一个接口,里面定义了一些抽象的方法,其目的就是对线性表的抽象,其中的方法就是线性表的一些常用基本运算。 而对于线性表的不同存储结构其实现方式就有所不同了,比如ArrayList是对线性表顺序存储结构的实现,LinkedList是线性表链式存储结构的实现等。存储结构没有确定我们就不知道数据怎么存储,但是对于线性表这种逻辑结构中数据的基本操作我们可以预知,无非就是获取长度、获取指定位置的数据、插入数据、删除数据等等操作,可以参考List。
对于本系列文章,只是对数据结构和一些常用算法学习,接下来的代码将选择性实现并分析算法。对线性表的抽象数据类型描述如下:
/**
* autour : openXu
* date : 2018/7/13 15:41
* className : IList
* version : 1.0
* description : 线性表的抽象数据类型
*/
public interface IList {
/**
* 判断线性表是否为空
* @return
*/
boolean isEmpty();
/**
* 获取长度
* @return
*/
int length();
/**
* 将结点添加到指定序列的位置
* @param index
* @param data
* @return
*/
boolean add(int index, T data);
/**
* 将指定的元素追加到列表的末尾
* @param data
* @return
*/
boolean add(T data);
/**
* 根据index移除元素
* @param index
* @return
*/
T remove(int index);
/**
* 移除值为data的第一个结点
* @param data
* @return
*/
boolean remove(T data);
/**
* 移除所有值为data的结点
* @param data
* @return
*/
boolean removeAll(T data);
/**
* 清空表
*/
void clear();
/**
* 设置指定序列元素的值
* @param index
* @param data
* @return
*/
T set(int index, T data);
/**
* 是否包含值为data的结点
* @param data
* @return
*/
boolean contains(T data);
/**
* 根据值查询索引
* @param data
* @return
*/
int indexOf(T data);
/**
* 根据data值查询最后一次出现在表中的索引
* @param data
* @return
*/
int lastIndexOf(T data);
/**
* 获取指定序列的元素
* @param index
* @return
*/
T get(int index);
/**
* 输出格式
* @return
*/
String toString();
}
2、线性表的顺序存储结构
2.1 顺序表
把线性表中的所有元素按照其逻辑顺序依次存储在计算机存储器中指定存储位置开始的一块连续的存储空间中。在Java中创建一个数组对象就是分配了一块可供用户使用的连续的存储空间,该存储空间的起始位置就是由数组名表示的地址常量。线性表的顺序存储结构是利用数组来实现的。
在Java中,我们通常利用下面的方式来使用数组:
int[] array = new int[]{1,2,3}; //创建一个数组
Array.getInt(array, 0); //获取数组中序列为0的元素
Array.set(array, 0, 1); //设置序列为0的元素值为1
这种方式创建的数组是固定长度的,其容量无法修改,当array被创建出来的时候,系统只为其分配3个存储空间,所以我们无法对其进行添加和删除操作。Array这个类里面提供了很多方法用于操作数组,这些方法都是静态的,所以Array是一个用于操作数组的工具类,这个类提供的方法只有两种:get和set,所以只能获取和设置数组中的元素,然后对于这两种操作,我们通常使用array[i]、array[i] = 0的简化方式,所以Array这个类用的比较少。
另外一种数组ArrayList,其内部维护了一个数组,所以本质上也是数组,其操作都是对数组的操作,与上述数组不同的是,ArrayList是一种可变长度的数组。既然数组创建时就已经分配了存储空间,为什么ArrayList是长度可变的呢?长度可变意味着可以从数组中添加、删除元素,向ArrayList中添加数据时,实际上是创建了一个新的数组,将原数组中元素一个个复制到新数组后,将新元素添加进来。如果ArrayList仅仅做了这么简单的操作,那他就不应该出现了。ArrayList中的数组长度是大于等于其元素个数的,当执行add()操作时首先会检查数组长度是否够用,只有当数组长度不够用时才会创建新的数组,由于创建新数组意味着老数据的搬迁,所以这个机制也算是利用空间换取时间上的效率。但是如果添加操作并不是尾部添加,而是头部或者中间位置插入,也避免不了元素位置移动。
2.2 顺序表基本运算的实现
/**
* autour : openXu
* date : 2018/7/11 10:45
* className : LinearArray
* version : 1.0
* description : 线性表的顺序存储结构(顺序表),是由数组来实现的
*/
public class LinearArray implements IList{
private Object[] datas;
/**
* 通过给定的数组 建立顺序表
* @param objs
* @return
*/
public static LinearArray createArray(T[] objs){
LinearArray array = new LinearArray();
array.datas = new Object[objs.length];
for(int i = 0; i= datas.length)
throw new IndexOutOfBoundsException();
return (T) datas[index];
}
/**
* 为指定索引的结点设置值
* 分析:时间复杂度O(1)
*/
@Override
public T set(int index, T data) {
if (index<0 || index >= datas.length)
throw new IndexOutOfBoundsException();
T oldValue = (T) datas[index];
datas[index] = data;
return oldValue;
}
/**
* 判断是否包含某值只需要判断该值有没有出现过
* 分析:时间复杂度O(n)
*/
@Override
public boolean contains(T data) {
return indexOf(data) >= 0;
}
/**
* 获取某值第一次出现的索引
* 分析:时间复杂度O(n)
*/
@Override
public int indexOf(T data) {
if (data == null) {
for (int i = 0; i < datas.length; i++)
if (datas[i]==null)
return i;
} else {
for (int i = 0; i < datas.length; i++)
if (data.equals(datas[i]))
return i;
}
return -1;
}
/**
* 获取某值最后一次出现的索引
* 分析:时间复杂度O(n)
*/
@Override
public int lastIndexOf(T data) {
if (data == null) {
for (int i = datas.length-1; i >= 0; i--)
if (datas[i]==null)
return i;
} else {
for (int i = datas.length-1; i >= 0; i--)
if (data.equals(datas[i]))
return i;
}
return -1;
}
/**
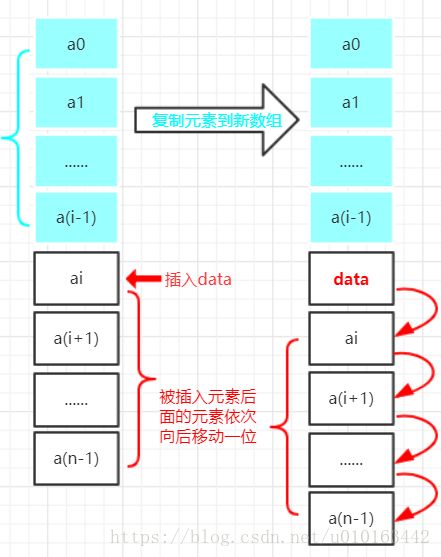
* 指定位置插入元素
* 分析:时间复杂度O(n)
* 在数组中插入元素时,需要创建一个比原数组容量大1的新数组,
* 将原数组中(0,index-1)位置的元素拷贝到新数组,指定新数组index位置元素值为新值,
* 继续将原数组(index, length-1)的元素拷贝到新数组
* @param index
* @param data
* @return
*/
@Override
public boolean add(int index, T data) {
if (index > datas.length || index < 0)
throw new IndexOutOfBoundsException();
Object destination[] = new Object[datas.length + 1];
System.arraycopy(datas, 0, destination, 0, index);
destination[index] = data;
System.arraycopy(datas, index, destination, index
+ 1, datas.length - index);
datas = destination;
return true;
}
/**
* 在顺序表末尾处插入元素
* 分析:时间复杂度O(n)
* 同上面一样,也需要创建新数组
* @param data
* @return
*/
@Override
public boolean add(T data) {
Object destination[] = new Object[datas.length + 1];
System.arraycopy(datas, 0, destination, 0, datas.length);
destination[datas.length] = data;
datas = destination;
return true;
}
/**
* 有序表添加元素
* @param data
* @return
*/
public boolean addByOrder(int data) {
int index = 0;
//找到顺序表中第一个大于等于data的元素
while(index= datas.length || index < 0)
throw new IndexOutOfBoundsException();
T oldValue = (T) datas[index];
fastRemove(index);
return oldValue;
}
/**
* 删除指定值的第一个元素
* @param data
* @return
*/
@Override
public boolean remove(T data) {
if (data == null) {
for (int index = 0; index < datas.length; index++)
if (datas[index] == null) {
fastRemove(index);
return true;
}
} else {
for (int index = 0; index < datas.length; index++)
if (data.equals(datas[index])) {
fastRemove(index);
return true;
}
}
return false;
}
/**
* 移除指定序列的元素
* @param index
*/
private void fastRemove(int index) {
Object destination[] = new Object[datas.length - 1];
System.arraycopy(datas, 0, destination, 0, index);
System.arraycopy(datas, index+1, destination, index,
datas.length - index-1);
datas = destination;
}
@Override
public boolean removeAll(T data) {
return false;
}
@Override
public void clear() {
datas = new Object[]{};
}
@Override
public String toString() {
if(isEmpty())
return "";
String str = "[";
for(int i = 0; i 算法分析:
插入元素:
删除元素:
3、线性表的链式存储结构
顺序表必须占用一整块事先分配大小固定的存储空间,这样不便于存储空间的管理。为此提出了可以实现存储空间动态管理的链式存储方式–链表。
3.1 链表
在链式存储中,每个存储结点不仅包含元素本身的信息(数据域),还包含元素之间逻辑关系的信息,即一个结点中包含有直接后继结点的地址信息,这称为指针域。这样可以通过一个结点的指针域方便的找到后继结点的位置。
由于顺序表中每个元素至多只有一个直接前驱元素和一个直接后继元素。当采用链式存储时,一种最简单也最常用的方法是:
在每个结点中除包含数据域外,只设置一个指针域用以指向其直接后继结点,这种构成的链接表称为线性单向链接表,简称单链表。
另一种方法是,在每个结点中除包含数值域外,设置两个指针域,分别用以指向直接前驱结点和直接后继结点,这样构成的链接表称为线性双向链接表,简称双链表。
单链表当访问一个结点后,只能接着访问它的直接后继结点,而无法访问他的直接前驱结点。双链表则既可以依次向后访问每个结点,也可以依次向前访问每个结点。
单链表结点元素类型定义:
public class LNode {
protected LNode next; //指针域,指向直接后继结点
protected Object data; //数据域
}
双链表结点元素类型定义:
public class DNode {
protected DNode prior; //指针域,指向直接前驱结点
protected DNode next; //指针域,指向直接后继结点
protected Object data; //数据域
}
在顺序表中,逻辑上相邻的元素,对应的存储位置也相邻,所以进行插入或删除操作时,通常需要平均移动半个表的元素,这是相当费时的操作。
在链表中,每个结点存储位置可以任意安排,不必要求相邻,插入或删除操作只需要修改相关结点的指针域即可,方便省时。对于单链表,如果要在结点p之前插入一个新结点,由于通过p并不能找到其前驱结点,我们需要从链表表头遍历至p的前驱结点然后进行插入操作,这样时间复杂度就是O(n),而顺序表插入删除结点时间复杂度也是O(n),那为什么说链表插入删除操作更加高效呢?因为单链表插入删除操作所消耗的时间主要在于查找前驱结点,这个查找工作的时间复杂度为O(n),而真正超如删除时间为O(1),还有顺序表需要移动结点,移动结点通常比单纯的查找更加费时,链表不需要连续的空间,不需要扩容创建新表,所以同样时间复杂度O(n),链表更适合插入和删除操作。对于遍历查找前驱结点的问题,在双链表中就能很好的解决,双链表在已知某结点的插入和删除操作时间复杂度是O(1)。
由于链表的每个结点带有指针域,从存储密度来讲,这是不经济的。所谓存储密度是指结点数据本身所占存储量和整改结点结构所占存储量之比。
3.2 单链表基本运算的实现
/**
* autour : openXu
* date : 2018/7/11 15:48
* className : LinkList
* version : 1.0
* description : 单链表基本实现
*/
public class LinkList implements IList{
public LNode head; //单链表开始结点
/**
* 1.1 创建单链表(头插法:倒序)
* 解:遍历数组,创建新结点,新结点的指针域指向头结点,让新结点作为头结点
* 时间复杂度O(n)
* @param array
* @return
*/
public static LinkList createListF(T[] array){
LinkList llist = new LinkList();
if(array!=null && array.length>0) {
for (T obj : array) {
LNode node = new LNode();
node.data = obj;
node.next = llist.head;
llist.head = node;
}
}
return llist;
}
/**
* 1.2 创建单链表(尾插法:顺序)
* 解:
* 时间复杂度O(n)
* @param array
* @return
*/
public static LinkList createListR(T[] array){
LinkList llist = new LinkList();
if(array!=null && array.length>0){
llist.head = new LNode();
llist.head.data = array[0];
LNode temp = llist.head;
for(int i = 1; i < array.length; i++){
LNode node = new LNode();
node.data = array[i];
temp.next = node;
temp = node;
}
}
return llist;
}
/**
* 判断单链表是否为空表
* 时间复杂度O(1)
* @return
*/
@Override
public boolean isEmpty() {
return head==null;
}
/**
* 4 获取单链表长度
* 时间复杂度O(n)
* @return
*/
@Override
public int length() {
if(head==null)
return 0;
int l = 1;
LNode node = head;
while(node.next!=null) {
l++;
node = node.next;
}
return l;
}
@Override
public void clear() {
head = null;
}
@Override
public T set(int index, T data) {
return null;
}
@Override
public boolean contains(T data) {
return false;
}
@Override
public T get(int index) {
return getNode(index).data;
}
/**
* 6.1 获取指定索引的结点
* 时间复杂度O(n)
* @param index
* @return
*/
public LNode getNode(int index){
LNode node = head;
int j = 0;
while(j < index && node!=null){
j++;
node = node.next;
}
return node;
}
/**
* 6.2 获取指定数据值结点的索引
* 时间复杂度O(n) 空间复杂度O(1)
* @param data
* @return
*/
@Override
public int indexOf(T data) {
if(head==null)
return -1; //没有此结点
LNode node = head;
int j = 0;
while(node!=null){
if(node.data.equals(data))
return j;
j++;
node = node.next;
}
return -1;
}
@Override
public int lastIndexOf(T data) {
if(head==null)
return -1;
int index = -1;
LNode node = head;
int j = 0;
while(node!=null){
if(node.data.equals(data)) {
index = j;
}
j++;
node = node.next;
}
return index;
}
/**
* 6.3 单链表中的倒数第k个结点(k > 0)
* 解:先找到顺数第k个结点,然后使用前后指针移动到结尾即可
* 时间复杂度O(n) 空间复杂度O(1)
* @param k
* @return
*/
public LNode getReNode(int k){
if(head==null)
return null;
int len = length();
if(k > len)
return null;
LNode target = head;
LNode next = head;
for(int i=0;i < k;i++)
next = next.next;
while(next!=null){
target = target.next;
next = next.next;
}
return target;
}
/**
* 6.4 查找单链表的中间结点
* 时间复杂度O(n) 空间复杂度O(1)
* @return
*/
public LNode getMiddleNode(){
if(head == null|| head.next == null)
return head;
LNode target = head;
LNode temp = head;
while(temp != null && temp.next != null){
target = target.next;
temp = temp.next.next;
}
return target;
}
/**
* 2.1 将单链表合并为一个单链表
* 解:遍历第一个表,用其尾结点指向第二个表头结点
* 时间复杂度O(n)
* @return
*/
public static LNode mergeList(LNode head1, LNode head2){
if(head1==null) return head2;
if(head2==null) return head1;
LNode loop = head1;
while(loop.next!=null) //找到list1尾结点
loop = loop.next;
loop.next = head2; //将list1尾结点指向list2头结点
return head1;
}
/**
* 2.1 通过递归,合并两个有序的单链表head1和head2
*
* 解:两个指针分别指向两个头结点,比较两个结点大小,
* 小的结点指向下一次比较结果(两者中较小),最终返回第一次递归的最小结点
* @param head1
* @param head2
* @return
*/
public static LNode mergeSortedListRec(LNode head1, LNode head2){
if(head1==null)return head2;
if(head2==null)return head1;
if (((int)head1.data)>((int)head2.data)) {
head2.next = mergeSortedListRec(head2.next, head1);
return head2;
} else {
head1.next = mergeSortedListRec(head1.next, head2);
return head1;
}
}
/**
* 3.1 循环的方式将单链表反转
* 时间复杂度O(n) 空间复杂度O(1)
*/
public void reverseListByLoop() {
if (head == null || head.next == null)
return;
LNode pre = null;
LNode nex = null;
while (head != null) {
nex = head.next;
head.next = pre;
pre = head;
head = nex;
}
head = pre;
}
/**
* 3.2 递归的方式将单链表反转,返回反转后的链表头结点
* 时间复杂度O(n) 空间复杂度O(n)
*/
public LNode reverseListByRec(LNode head) {
if(head==null||head.next==null)
return head;
LNode reHead = reverseListByRec(head.next);
head.next.next = head;
head.next = null;
return reHead;
}
/**
* 5.1 获取单链表字符串表示
* 时间复杂度O(n)
*/
@Override
public String toString() {
if(head == null)
return "";
LNode node = head;
StringBuffer buffer = new StringBuffer();
while(node != null){
buffer.append(node.data+" -> ");
node = node.next;
}
return buffer.toString();
}
public static String display(LNode head){
if(head == null)
return "";
LNode node = head;
StringBuffer buffer = new StringBuffer();
while(node != null){
buffer.append(" -> "+node.data);
node = node.next;
}
return buffer.toString();
}
/**
* 5.2 用栈的方式获取单链表从尾到头倒叙字符串表示
* 解:由于栈具有先进后出的特性,现将表中的元素放入栈中,然后取出就倒序了
* 时间复杂度O(n) 空间复杂度O(1)
* @return
*/
public String displayReverseStack(){
if(head == null)
return "";
Stack stack = new Stack < >(); //堆栈 先进先出
LNode head = this.head;
while(head!=null){
stack.push(head);
head=head.next;
}
StringBuffer buffer = new StringBuffer();
while(!stack.isEmpty()){
//pop()移除堆栈顶部的对象,并将该对象作为该函数的值返回。
buffer.append(" -> "+stack.pop().data);
}
return buffer.toString();
}
/**
* 5.3 用递归的方式获取单链表从尾到头倒叙字符串表示
* @return
*/
public void displayReverseRec(StringBuffer buffer, LNode head){
if(head==null)
return;
displayReverseRec(buffer, head.next);
buffer.append(" -> ");
buffer.append(head.data);
}
/**
* 7.1 插入结点
* 解:先找到第i-1个结点,让创建的新结点的指针域指向第i-1结点指针域指向的结点,
* 然后将i-1结点的指针域指向新结点
* 时间复杂度O(n) 空间复杂度O(1)
* @param data
* @param index
*/
@Override
public boolean add(int index, T data) {
if(index==0){ //插入为头结点
LNode temp = new LNode();
temp.next = head;
return true;
}
int j = 0;
LNode node = head;
while(j < index-1 && node!=null){ //找到序列号为index-1的结点
j++;
node = node.next;
}
if(node==null)
return false;
LNode temp = new LNode(); //创建新结点
temp.data = data;
temp.next = node.next; //新结点插入到Index-1结点之后
node.next = temp;
return true;
}
@Override
public boolean add(T data) {
LNode node = head;
while(node!=null && node.next!=null) //找到尾结点
node = node.next;
LNode temp = new LNode(); //创建新结点
temp.data = data;
node.next = temp;
return false;
}
@Override
public T remove(int index) {
LNode node = deleteNode(index);
return node==null?null:node.data;
}
/**
* 7.2 删除结点
* 解:让被删除的结点前一个结点的指针域指向后一个结点指针域
* 时间复杂度O(n) 空间复杂度O(1)
* @return
*/
public LNode deleteNode(int index){
LNode node = head;
if(index==0){ //删除头结点
if(node==null)
return null;
head = node.next;
return node;
}
//非头结点
int j = 0;
while(j < index-1 && node!=null){ //找到序列号为index-1的结点
j++;
node = node.next;
}
if(node==null)
return null;
LNode delete = node.next;
if(delete==null)
return null; //不存在第index个结点
node.next = delete.next;
return delete;
}
@Override
public boolean remove(T data) {
return false;
}
@Override
public boolean removeAll(T data) {
return false;
}
/**
* 7.3 给出一单链表头指针head和一节点指针delete,要求O(1)时间复杂度删除节点delete
* 解:将delete节点value值与它下个节点的值互换的方法,
* 但是如果delete是最后一个节点,需要特殊处理,但是总得复杂度还是O(1)
* @return
*/
public static void deleteNode(LNode head, LNode delete){
if(delete==null)
return;
//首先处理delete节点为最后一个节点的情况
if(delete.next==null){
if(head==delete) //只有一个结点
head = null;
else{
//删除尾结点
LNode temp = head;
while(temp.next!=delete)
temp = temp.next;
temp.next=null;
}
} else{
delete.data = delete.next.data;
delete.next = delete.next.next;
}
return;
}
/**
* 8.1 判断一个单链表中是否有环
* 解:使用快慢指针方法,如果存在环,两个指针必定指向同一结点
* 时间复杂度O(n) 空间复杂度O(1)
* @return
*/
public static boolean hasCycle(LNode head){
LNode p1 = head;
LNode p2 = head;
while(p1!=null && p2!=null){
p1 = p1.next; //一次跳一步
p2 = p2.next.next; //一次跳两步
if(p2 == p1)
return true;
}
return false;
}
/**
* 8.2、已知一个单链表中存在环,求进入环中的第一个节点
* 利用hashmap,不要用ArrayList,因为判断ArrayList是否包含某个元素的效率不高
* @param head
* @return
*/
public static LNode getFirstNodeInCycleHashMap(LNode head){
LNode target = null;
HashMap map=new HashMap< >();
while(head != null){
if(map.containsKey(head)) {
target = head;
break;
} else {
map.put(head, true);
head = head.next;
}
}
return target;
}
/**
* 8.3、已知一个单链表中存在环,求进入环中的第一个节点,不用hashmap
* 用快慢指针,与判断一个单链表中是否有环一样,找到快慢指针第一次相交的节点,
* 此时这个节点距离环开始节点的长度和链表头距离环开始的节点的长度相等
* 参考 https://www.cnblogs.com/fankongkong/p/7007869.html
* @param head
* @return
*/
public static LNode getFirstNodeInCycle(LNode head){
LNode fast = head;
LNode slow = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
if(slow == fast)
break;
}
if(fast == null||fast.next == null)
return null;//判断是否包含环
//相遇节点距离环开始节点的长度和链表投距离环开始的节点的长度相等
slow=head;
while(slow!=fast){
slow=slow.next;
fast=fast.next;
}//同步走
return slow;
}
/**
* 9、判断两个单链表是否相交,如果相交返回第一个节点,否则返回null
* ①、暴力遍历两个表,是否有相同的结点(时间复杂度O(n²))
* ②、第一个表的尾结点指向第二个表头结点,然后判断第二个表是否存在环,但不容易找出交点(时间复杂度O(n))
* ③、两个链表相交,必然会经过同一个结点,这个结点的后继结点也是相同的(链表结点只有一个指针域,后继结点只能有一个),
* 所以他们的尾结点必然相同。两个链表相交,只能是前面的结点不同,所以,砍掉较长链表的差值后同步遍历,判断结点是否相同,相同的就是交点了。
* 时间复杂度(时间复杂度O(n))
* @param list1
* @param list2
* @return 交点
*/
public static LNode isIntersect(LinkList list1, LinkList list2){
LNode head1 = list1.head;
LNode head2 = list2.head;
if(head1==null || head2==null)return null;
int len1 = list1.length();
int len2 = list2.length();
//砍掉较长链表的差值
if(len1 >= len2){
for(int i=0;i < len1-len2;i++){
head1=head1.next;
}
}else{
for(int i=0;i < len2-len1;i++){
head2=head2.next;
}
}
//同步遍历
while(head1 != null&&head2 != null){
if(head1 == head2)
return head1;
head1=head1.next;
head2=head2.next;
}
return null;
}
}
算法分析
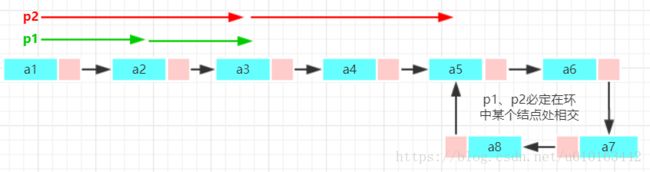
判断一个单链表中是否有环(尾结点指向过往结点):
我们可以通过HashMap判断,遍历结点,将结点值放入HashMap,如果某一刻发现当前结点在map中已经存在,则存在环,并且此结点正是环的入口,此算法见8.2方法。但是有一种问法是不通过任何其他数据结构怎么判断单链表是否存在环。
这样我们可利用的就只有单链表本身,一种解法是通过快慢指针,遍历链表,一个指针跳一步(慢指针步长为1),另一个指针跳两步(快指针步长为2),如果存在环,这两个指针必将在某一刻指向同一结点,假设此时慢指针跳了n步,则快指针跳的步数为n/2步:
判断两个单链表是否相交:
由于单链表的特性(只有一个指针域),如果两个表相交,那必定是Y形相交,不会是X形相交,如图所示。两个单链表后面的结点相同,不同的部分只有前面,砍掉较长的链表的前面部分,然后两个链表同步遍历,必将指向同一个结点,这个结点就是交点:
3.3 双链表
双链表中每个结点有两个指针域,一个指向其直接后继结点,一个指向其直接前驱结点。
建立双链表也有两种方法,头插法和尾插法,这与创建单链表过程相似。在双链表中,有些算法如求长度、取元素值、查找元素等算法与单链表中相应算法是相同的。但是在单链表中,进行结点插入和删除时涉及前后结点的一个指针域的变化,而双链表中结点的插入和删除操作涉及前后结点的两个指针域的变化。java中LinkedList正是对双链表的实现,算法可参考此类。
双链表基本运算的实现
/**
* autour : openXu
* date : 2018/7/11 15:48
* className : LinkList
* version : 1.0
* description : 双链表基本实现
*/
public class DLinkList implements IList{
transient DNode first; //双链表开始结点
transient DNode last; //双链表末端结点
private int size; //结点数
/**
* 创建单链表(头插法:倒序)
* 时间复杂度O(n)
* @param array
* @return
*/
public static DLinkList createListF(T[] array){
DLinkList dlist = new DLinkList();
if(array!=null && array.length>0) {
dlist.size = array.length;
for (T obj : array) {
DNode node = new DNode();
node.data = obj;
node.next = dlist.first;
if(dlist.first!=null)
dlist.first.prior = node; //相比单链表多了此步
else
dlist.last = node;
dlist.first = node;
}
}
return dlist;
}
/**
* 1.2 创建单链表(尾插法:顺序)
* 时间复杂度O(n)
* @param array
* @return
*/
public static DLinkList createListR(T[] array){
DLinkList dlist = new DLinkList();
if(array!=null && array.length>0){
dlist.size = array.length;
dlist.first = new DNode();
dlist.first.data = array[0];
dlist.last = dlist.first;
for(int i = 1; i < array.length; i++){
DNode node = new DNode();
node.data = array[i];
dlist.last.next = node;
node.prior = dlist.last; //相比单链表多了此步
dlist.last = node;
}
}
return dlist;
}
@Override
public boolean isEmpty() {
return size==0;
}
@Override
public int length() {
return size;
}
/**2 添加结点*/
@Override
public boolean add(int index, T data) {
if(index < 0 || index > size)
throw new IndexOutOfBoundsException();
DNode newNode = new DNode();
newNode.data = data;
if (index == size) { //在末尾添加结点不需要遍历
final DNode l = last;
if (l == null) //空表
first = newNode;
else {
l.next = newNode;
newNode.prior = l;
}
last = newNode;
size++;
} else {
//其他位置添加结点需要遍历找到index位置的结点
DNode indexNode = getNode(index);
DNode pred = indexNode.prior;
newNode.prior = pred;
newNode.next = indexNode;
indexNode.prior = newNode;
if (pred == null)
first = newNode;
else
pred.next = newNode;
size++;
}
return false;
}
@Override
public boolean add(T data) {
return add(size, data);
}
/**3 删除结点*/
@Override
public T remove(int index) {
if(index < 0 || index >= size)
throw new IndexOutOfBoundsException();
return unlink(getNode(index));
}
@Override
public boolean remove(T data) {
if (data == null) {
for (DNode x = first; x != null; x = x.next) {
if (x.data == null) {
unlink(x);
return true;
}
}
} else {
for (DNode x = first; x != null; x = x.next) {
if (data.equals(x.data)) {
unlink(x);
return true;
}
}
}
return false;
}
@Override
public boolean removeAll(T data) {
boolean result = false;
if (data == null) {
for (DNode x = first; x != null; x = x.next) {
if (x.data == null) {
unlink(x);
result = true;
}
}
} else {
for (DNode x = first; x != null; x = x.next) {
if (data.equals(x.data)) {
unlink(x);
result = true;
}
}
}
return result;
}
/**
* 将指定的结点解除链接
* @param x
* @return
*/
private T unlink(DNode x) {
// assert x != null;
final T element = x.data;
final DNode next = x.next;
final DNode prev = x.prior;
if (prev == null) {
first = next;
} else {
prev.next = next;
x.prior = null;
}
if (next == null) {
last = prev;
} else {
next.prior = prev;
x.next = null;
}
x.data = null;
size--;
return element;
}
/**
* 清空
*/
@Override
public void clear() {
for (DNode x = first; x != null; ) {
DNode next = x.next;
x.data = null;
x.next = null;
x.prior = null;
x = next;
}
first = last = null;
size = 0;
}
/**
* 设置结点值
* @param index
* @param data
* @return
*/
@Override
public T set(int index, T data) {
if(index < 0 || index >= size)
throw new IndexOutOfBoundsException();
DNode x = getNode(index);
T oldVal = x.data;
x.data = data;
return oldVal;
}
/**
* 判断是否存在结点值
* @param data
* @return
*/
@Override
public boolean contains(T data) {
return indexOf(data) != -1;
}
/**
* 检索结点值
* @param data
* @return
*/
@Override
public int indexOf(T data) {
int index = 0;
if (data == null) {
for (DNode x = first; x != null; x = x.next) {
if (x.data == null)
return index;
index++;
}
} else {
for (DNode x = first; x != null; x = x.next) {
if (data.equals(x.data))
return index;
index++;
}
}
return -1;
}
@Override
public int lastIndexOf(T data) {
int index = size;
if (data == null) {
for (DNode x = last; x != null; x = x.prior) {
index--;
if (x.data == null)
return index;
}
} else {
for (DNode x = last; x != null; x = x.prior) {
index--;
if (data.equals(x.data))
return index;
}
}
return -1;
}
@Override
public T get(int index) {
if(index < 0 || index >= size)
throw new IndexOutOfBoundsException();
return getNode(index).data;
}
/**
* 获取指定索引的结点
* 解:由于双链表能双向检索,判断index离开始结点近还是终端结点近,从近的一段开始遍历
* 时间复杂度O(n)
* @param index
* @return
*/
private DNode getNode(int index) {
if (index < (size >> 1)) {
DNode x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
DNode x = last;
for (int i = size - 1; i > index; i--)
x = x.prior;
return x;
}
}
/**
* 倒序
* 遍历每个结点,让node.next = node.prior; node.prior = (node.next此值需要体现保存);
*/
public void reverse(){
last = first; //反转后终端结点=开始结点
DNode now = first;
DNode next;
while(now!=null){
next = now.next; //保存当前结点的后继结点
now.next = now.prior;
now.prior = next;
first = now;
now = next;
}
}
@Override
public String toString() {
if(size == 0)
return "";
DNode node = first;
StringBuffer buffer = new StringBuffer();
buffer.append(" ");
while(node != null){
buffer.append(node.data+" -> ");
node = node.next;
}
buffer.append("next\npre");
node = last;
int start = buffer.length();
LogUtil.i(getClass().getSimpleName(), "buffer长度:"+buffer.length());
while(node != null){
buffer.insert(start ," <- "+node.data);
node = node.prior;
}
return buffer.toString();
}
}
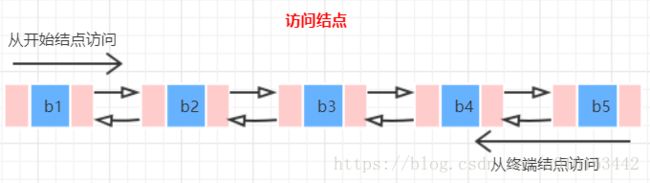
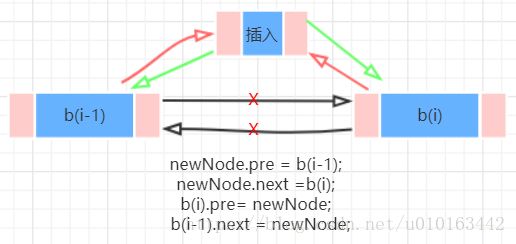
算法分析
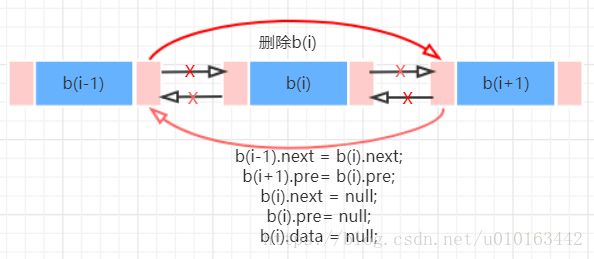
双链表与单链表不同之处在于,双链表能从两端依次访问各个结点。单链表相对于顺序表优点是插入、删除数据更方便,但是访问结点需要遍历,时间复杂度为O(n);双链表就是在单链表基础上做了一个优化,使得访问结点更加便捷(从两端),这样从近的一端出发时间复杂度变为O(n/2),虽然不是指数阶的区别,但也算是优化。双链表在插入、删除结点时逻辑比单链表稍麻烦:
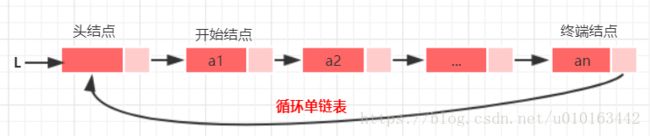
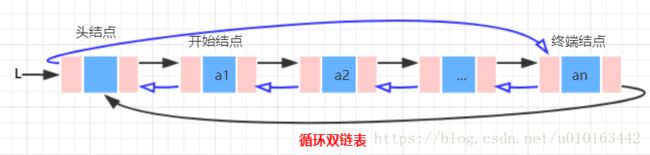
3.4 循环链表
循环链表是另一种形式的链式存储结构,它的特点是表中尾结点的指针域不再是空,而是指向头结点,整个链表形成一个环。由此,从表中任意一结点出发均可找到链表中其他结点。如图所示为带头结点的循环单链表和循环双链表:
4、有序表
所谓有序表,是指所有结点元素值以递增或递减方式排列的线性表,并规定有序表中不存在元素值相同的结点。
有序表可以采用顺序表和链表进行存储,若以顺序表存储有序表,其算法除了add(T data)以外,其他均与前面说的顺序表对应的运算相同。有序表的add(T data)操作不是插入到末尾,而需要遍历比较大小后插入相应位置。
public boolean addByOrder(int data) {
int index = 0;
//找到顺序表中第一个大于等于data的元素
while(index