Huffman编码
1. 概念
我们来学习一种能够大幅压缩自然语言文件空间(以及许多其他类型文件)的数据压缩技巧。它的主要思想是放弃文本文件的普通保存方式:不再使用 7 位或 8 位二进制数表示每一个字符,而是使用较少的比特表示出现频率高的字符,用较多的比特表示出现频率低的字符。
为了更形象地说明这个概念,先来看一个例子。我们现在对字符串 ABRACADABRA! 编码,由 7 位 ASCII 字符编码可以得到比特字符串:
100000110000101010010100000110000111000001100010010000011000010101001010000010100001
要将这段比特字符串解码,每次只需读取 7 位并根据 ASCII 编码表即可将其转换为字符。在这种标准的编码下,只出现一次的 D 和出现了 5 次的 A 所需的比特数是一样的。霍夫曼压缩的思想是通过用较少的比特表示出现频率高的字符,用较多的比特表示出现频率低的字符,这样字符串所使用的总比特数就会降低。
1.1 变长前缀码
我们可以将最短的比特字符串赋值于最常用的字符,于是有:
| 字符 | 编码 | 频率 | 总位数 |
|---|---|---|---|
| A | 0 | 5 | 5 |
| B | 1 | 2 | 2 |
| R | 00 | 2 | 4 |
| C | 01 | 1 | 2 |
| D | 10 | 1 | 2 |
| ! | 11 | 1 | 2 |
| 总数 | - | - | 17 |
这样字符串 ABRACADABRA! 的编码就是 0 1 00 0 01 0 10 0 1 00 0 11。这种表示方法只用了 17 位,而 7 为的 ASCII 编码则用了 84 位。但这种表示方法并不完整,因为它需要分隔符来区分字符。但是,17 位加上 11 个分隔符也比标准的编码要紧凑的多,没有用于编码的比特字符不会在这条消息中出现。
如果所有字符编码都不会成为其他字符编码的前缀,那么就不需要分隔符了,含有这种性质的编码规则叫作前缀码。例如,我们进行如下编码:
| 字符 | 编码 | 频率 | 总位数 |
|---|---|---|---|
| A | 0 | 5 | 5 |
| B | 1111 | 2 | 8 |
| C | 110 | 1 | 3 |
| D | 100 | 1 | 3 |
| R | 1110 | 2 | 8 |
| ! | 101 | 1 | 3 |
| 总数 | - | - | 30 |
那么将以下长为 30 的比特字符串解码的方式就只有字符串 ABRACADABRA! 一种了:
011111110011001000111111100101
所有的前缀码的解码方式都和它一样,是唯一的(不需要任何分隔符),因此前缀码广泛用于生产中。像上述 7 位 ASCII 编码这样的定长编码也是前缀码。
1.2 前缀码的单词查找树
表示前缀码的一种简便方法就是使用单词查找树。任意含有 M 个空链接的单词查找树都为 M 个字符定义了一种前缀码方法:我们将空链接替换为指向叶子节点(含有两个空链接的节点)的链接,每个叶子节点都含有一个需要编码的字符。这样,每个字符的编码就是从根节点到该节点的路径表示的比特字符串,其中左链接表示 0,右链接表示 1。如图 1 显示了字符串 ABRACADABRA! 中的字符的两种前缀码。
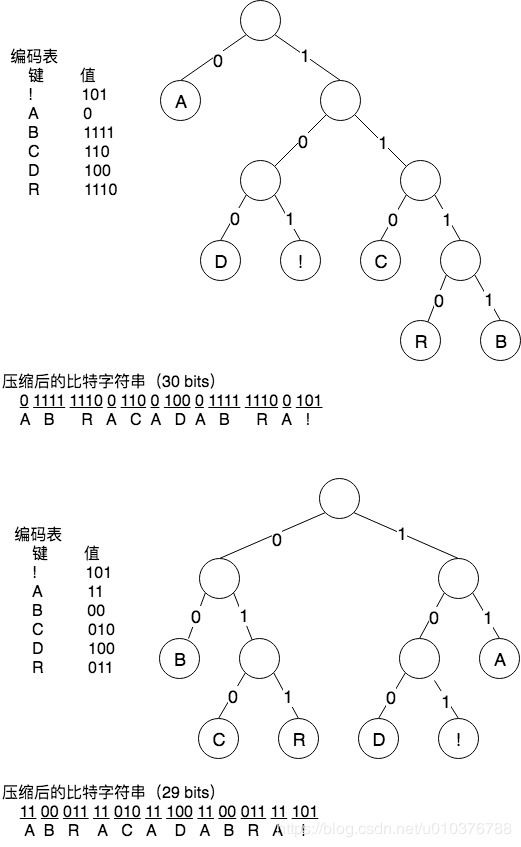
是否存在能够压缩得更多的单词查找树?如何才能找到压缩率更高的前缀码?寻找最优前缀码的通用方法是 David Albert Huffman 在 1952 年发明的,那时候他还是一个学生!这种方法的名称也就是霍夫曼编码。
2. 霍夫曼编码
2.1 单词查找树的节点
单词查找树和二叉树的定义类似,不过多了一个实例变量 frequency,用于保存字符出现的频率。另一个实例变量 aChar 用于表示叶子节点中需要被编码的字符。
private static class Node implements Comparable<Node>{
private final char aChar; // 单词查找树中的节点,非叶子节点不会使用该变量
private final int frequency; // 被编码字符出现的频率
private final Node left;
private final Node right;
public Node(char aChar, int frequency, Node left, Node right) {
this.aChar = aChar;
this.frequency = frequency;
this.left = left;
this.right = right;
}
@Override
public int compareTo(Node that) {
return this.frequency - that.frequency;
}
private boolean isLeaf(){
return (left == null) && (right == null);
}
}
2.2 单词查找树的构造
在构造过程中,我们将需要被编码的字符串放在叶子节点中并在每个节点中维护一个名为 frequency 的实例变量来表示以它为根节点的子树中的所有字符出现的频率。构造的第一步是创建一片由许多只有一个节点(即叶子节点)的树所组成的森林。每棵树都表示输入流中的一个字符,每个节点中的 frequency 变量的值都表示了它在输入流中的出现频率。接下来,自底向上根据频率构造这棵编码的单词查找树。在构造时,将它看作一棵节点中含有频率信息的二叉树;在构造后,我们才将它看作一棵用于编码的单词查找树。构造过程如下:首先找到两个频率最小的节点,然后创建一个以二者为子节点的新节点(新节点的频率值是它两个子节点的频率值之和)。这个操作会将森林中树的数量减一。然后不断重复这个过程,找到森林中的两棵频率最小的树并用相同的方式创建一个新的节点(每一步都会删除两棵树,添加一棵新树)。用优先级队列可以轻易的实现这个过程。简而言之,单词查找树的构造需要如下几个步骤:
- 统计被编码的字符出现的频率;
- 将每个字符构建成的只有一个节点的树,然后组成一个森林。
- 通过循环合并两棵频率最小的树,构造单词查找树,直到构造成一棵单词查找树。
下面用于一个具体的例子进行说明,假设现在我们需要对字符串 ABRACADABRA! 进行编码。第一步,统计被编码的字符出现的频率,将每个字符构建成的只有一个节点的树,然后组成一个森林,并放入优先级队列中,如图2:

自底向上根据频率构造这棵编码的单词查找树,找到两个频率最小的节点 ! 和节点 C,并从优先级队列中删除,然后创建一个以二者为子节点的新节点,该节点频率是 1 + 1 = 2,重新放到优先级队列中,如图3:
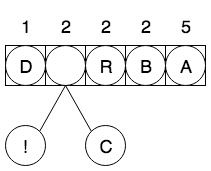
重复这个过程,找到森林中的两棵频率最小树,并用相同的方式创建一个新的节点,该节点的频率是 1 + 2 = 3,重新放到优先级队列中,如图4:
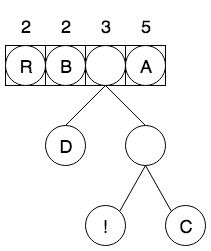
继续重复这个过程,找到森林中的两棵频率最小树,并用相同的方式创建一个新的节点,该节点的频率是 2 + 2 = 4,重新放到优先级队列中,如图5:

继续重复这个过程,找到森林中的两棵频率最小树,并用相同的方式创建一个新的节点,该节点的频率是 3 + 4 = 7,重新放到优先级队列中,如图6:
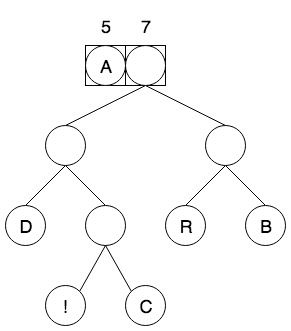
继续重复这个过程,找到森林中的两棵频率最小树,并用相同的方式创建一个新的节点,该节点的频率是 5 + 7 = 12,重新放到优先级队列中,如图7:
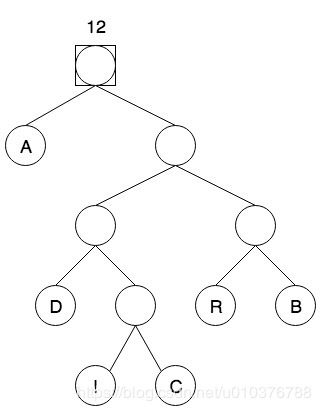
到此为止,优先级队列中只有一棵树,即为单词查找树。
2.3 前缀码压缩
在压缩时,我们使用单词查找树定义的编码来构造编码表。对于任意单词查找树,它都能产生一张将树中的字符和比特字符串(用 0 和 1 组成的 String 字符串表示)相对应的编码表。编码表就是一张将每个字符和它的比特字符串相关联的符号表:为了提升效率,我们使用一个由字符索引的数组 table[] 而非普通的符号表或 Map 字典,因为字符的数量并不多。在构造该符号表的时候,递归遍历整棵树并为每个节点维护一条从根节点到它的路径所对应的二进制字符串(0 表示左链接,1 表示右链接)。每当到达一个叶子节点时,算法就将节点的编码设为该二进制字符串。编码表建立之后,压缩也就很简单了,只需在其中查找输入字符所对应的编码即可。代码如下所示:
private void buildCode(String[] table, Node node, String str){
if (node.isLeaf()){
table[node.aChar] = str;
} else {
buildCode(table, node.left, str + '0');
buildCode(table, node.right, str + '1');
}
}
通过上一节构造的单词查找树,我们可以计算出字符串 ABRACADABRA! 的编码表。
| 字符 | 编码 | 频率 | 总位数 |
|---|---|---|---|
| ! | 1010 | 1 | 4 |
| A | 0 | 5 | 5 |
| B | 111 | 2 | 6 |
| C | 1011 | 1 | 4 |
| D | 100 | 1 | 3 |
| R | 110 | 2 | 6 |
| 总数 | - | - | 28 |
使用霍夫曼编码最后需要的比特位是 28,而标准的 7 位 ASCII 编码压缩需要的比特位是 84,大大减少了空间浪费。
综上所述,霍夫曼编码是一种高效的压缩算法,它是一种贪婪算法,因为它在每一步只是简单从集合中取出两个权值最小的树进行合并。
霍夫曼编码参考代码
public class Huffman {
// alphabet size of extended ASCII
private static final int ASCII = 256;
public void compress(String str){
char[] input = str.toCharArray();
int[] frequency = new int[ASCII];
// 1.统计被编码的字符出现的频率
for (int i = 0; i < input.length; i++){
frequency[input[i]]++;
}
// 2.将每个字符构建成的只有一个节点的树,组成一个森林。通过循环合并两颗频率最小的树,构造霍夫曼树
Node root = buildTrie(frequency);
// 3.构造编码表
String[] table = new String[ASCII];
buildCode(table, root, "");
// 打印编码表
for (int i = 0; i < table.length; i++){
if (table[i] != null){
System.out.printf("%c\t%s\n", i, table[i]);
}
}
}
/**
* 将字符出现的频率制成编码表
*/
private void buildCode(String[] table, Node node, String str){
if (node.isLeaf()){
table[node.aChar] = str;
} else {
buildCode(table, node.left, str + '0');
buildCode(table, node.right, str + '1');
}
}
/**
* 构建单词查找树
*/
private Node buildTrie(int[] frequency){
Queue<Node> queue = new PriorityQueue<>();
// 将每个被编码的字符构造的只有一个节点的树组成一片森林,放入优先级队列
for (char c = 0; c < ASCII; c++){
if (frequency[c] > 0){
queue.add(new Node(c, frequency[c], null, null));
}
}
// 将只有一个频率非0的字符构造成一颗树
if (queue.size() == 1){
if (frequency['\0'] == 0){
queue.add(new Node('\0', 0, null, null));
} else {
queue.add(new Node('\1', 0, null, null));
}
}
while (queue.size() > 1){
// 合并两颗频率最小的树
Node x = queue.poll();
Node y = queue.poll();
Node parent = new Node('\0', x.frequency + y.frequency, x, y);
queue.add(parent);
}
return queue.poll();
}
private static class Node implements Comparable<Node>{
private final char aChar;
private final int frequency;
private final Node left;
private final Node right;
public Node(char aChar, int frequency, Node left, Node right) {
this.aChar = aChar;
this.frequency = frequency;
this.left = left;
this.right = right;
}
@Override
public int compareTo(Node that) {
return this.frequency - that.frequency;
}
private boolean isLeaf(){
return (left == null) && (right == null);
}
}
public static void main(String[] args) {
Huffman huffman = new Huffman();
huffman.compress("ABRACADABRA!");
}
}
