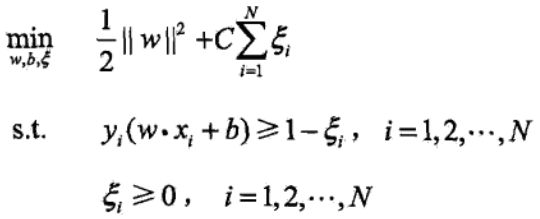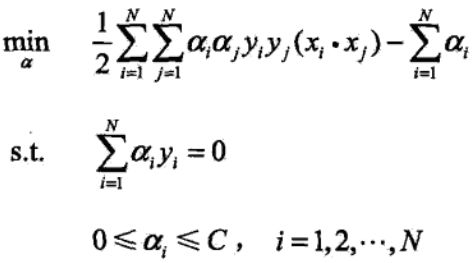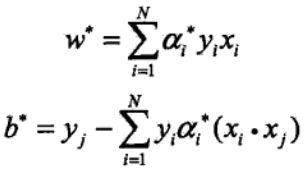机器学习教程之9-SVM的sklearn实现

0.概述

优点：支持向量机（Support Vector Machine，SVM）本质上是非线性方法，在样本量较少的时候，容易抓住数据和特征之间的非线性关系（相比线性分类方法如逻辑回归），因此可以解决非线性问题、可以避免神经网络结构选择和局部极小点问题、可以提高泛化性能、可以解决高维问题。

缺点：SVM对缺失数据敏感，对非线性问题没有通用解决方案，必须谨慎选择核函数来处理，计算复杂度高。

支持向量机（support vector machines,SVM）是一种二类分类模型。

SVM的基本模型是定义在特征空间的间隔最大的线性分类器，间隔最大使它有别于感知器。

SVM学习方法由简至繁分为三种模型：线性可分支持向量机、线性支持向量机及非线性支持向量机。分别对应三种处理方法：硬间隔最大化、软间隔最大化、核技巧。

支持向量机的学习是在特征空间进行的。

1.线性可分支持向量机与硬间隔最大化

线性可分支持向量机利用间隔最大化求最大化求最优分离超平面，这时解是唯一的。

从这“线性可分支持向量机学习算法-最大间隔法”可以看出求解约束最优化问题是最关键的问题。

可以证明最大间隔分离超平面是存在并且唯一的[1]。

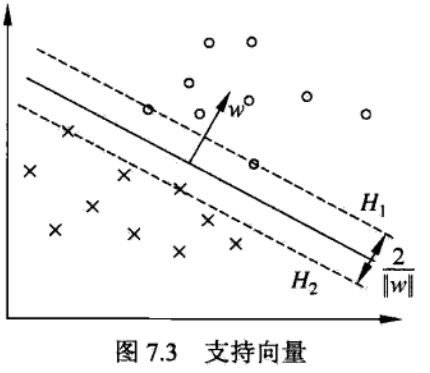
在线性可分情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量（support vector）。

支持向量是满足如下约束条件的点：

间隔为2/(w的范数)。

支持向量和间隔的图形化表达如下图：

在决定分离超平面时只有支持向量起作用，而其他实例点并不起作用。

应用拉格朗日对偶性，通过求解对偶问题（dual probleam）得到原始问题（primal problem）的最优解，这就是线性可分支持向量机的对偶问题。这样做的优点一是对偶问题往往更容易求解；二是自然引入核函数，进而推广到非线性分类问题。

通过对偶问题求解原始问题的具体算法如下：

实例如下：

2.线性”不可分“支持向量机与软间隔最大化

当训练数据中有一些特异点（outlier），将这些特异点除去后，剩下大部分的样本点组成的集合是线性可分的。

为了继续用线性可分支持向量机的方法解决线性”不可分“支持向量机的问题，引进一个松弛变量。

线性“不可分”支持向量机的原始问题为：

可以证明w的解是唯一的，但b的解存在于一个区间。

由于现实中训练数据集往往是线性不可分的，线性“不可分”支持向量机具有更广泛的适用性。

原始问题的对偶问题是：

阿法与w、b的关系式为：

总结线性（不可分）支持向量机学习算法：

3.相关数学基础

二次型与正定矩阵

正定矩阵

格莱姆矩阵

内积的定义

赋范向量空间

4.非线性支持向量机与核函数

非线性的例子：椭圆曲线

非线性可分问题：可以用超曲面分类。

通常利用非线性变换，将非线性问题转化为线性问题，通过解变换后的线性问题的方法求解原来的非线性问题。

用线性分类方法求解非线性分类问题分为两步：首先使用一个变换将原空间的数据映射到新空间；然后在新空间里用线性分类学习方法从训练数据中学习分类模型。核技巧就属于这样的方法。

核技巧应用到支持向量机，其基本想法就是通过一个非线性变换将输入空间（欧式空间或离散空间）队友于一个特征空间（希尔伯特空间），使得在输入空间中的超曲面对应于特征空间中的超平面（支持向量机）。

核函数的定义：

通过例子说明核函数和映射函数的关系：

对上例进行说明：

1）本例已知 输入空间的维度、核函数的表达式，要求其特征空间和映射;
2）解题思路为先取特征空间的维度，然后根据输入空间的维度将核函数展开，然后确定映射，映射的表达式为向量的形式。

非线性支持向量机学习算法：

5.序列最小最优化（sequential minimal optimization，SMO）算法

SMO算法的作用是高效地实现支持向量机学习。

SMO算法：

6.自问自答

根据“线性可分支持向量机学习算法-最大间隔法”，问自己几个问题：

1）如何求解约束最优化问题？

2）线性（不可分）支持向量里支持向量这个概念有什么用？

3）合页损失函数的概念是什么？有什么用？

4）非线性变换具体手段有哪些？

5）核函数是怎么来的？
答：在实际应用中，往往依赖领域知识直接选择核函数，核函数选择的有效性需要通过实验验证。

6）为什么直接计算K(x,z)比较容易，而通过”fai”(x)和”fai”(z)计算K(x,z)并不容易？

7.代码

1）SVM-LinearSVC.ipynb-线性分类SVM，iris数据集分类，正确率100%

"""
功能：实现线性分类支持向量机
说明：可以用于二类分类，也可以用于多类分类
作者：唐天泽
博客：http://write.blog.csdn.net/mdeditor#!postId=76188190
日期：2017-08-09
"""

# 导入本项目所需要的包
import pandas as pd
import numpy as np

from sklearn import datasets

from sklearn import svm

# 使用交叉验证的方法，把数据集分为训练集合测试集
from sklearn.model_selection import train_test_split

# 加载iris数据集
def load_data():
    iris = datasets.load_iris()
    """展示数据集的形状
       diabetes.data.shape, diabetes.target.shape
    """

    # 将数据集拆分为训练集和测试集 
    X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, test_size=0.10, random_state=0)
    return X_train, X_test, y_train, y_test

# 使用LinearSVC考察线性分类SVM的预测能力
def test_LinearSVC(X_train,X_test,y_train,y_test):

    # 选择模型
    cls = svm.LinearSVC()

    # 把数据交给模型训练
    cls.fit(X_train,y_train)

    print('Coefficients:%s, intercept %s'%(cls.coef_,cls.intercept_))
    print('Score: %.2f' % cls.score(X_test, y_test))

if __name__=="__main__":
    X_train,X_test,y_train,y_test=load_data() # 生成用于分类的数据集
    test_LinearSVC(X_train,X_test,y_train,y_test) # 调用 test_LinearSVC

Coefficients:[[ 0.18423605 0.45122452 -0.8079452 -0.45071742]
[-0.13677264 -0.74522629 0.57271527 -1.11271932]
[-0.79430688 -0.95801471 1.31460254 1.81712983]], intercept [ 0.10956188 1.8666474 -1.72578128]
Score: 1.00

2) SVM-LinearSVC-kaggle.ipynb-线性分类SVM，手写数字数据集分类，正确率85%

"""
"""
功能：实现线性分类支持向量机
说明：可以用于二类分类，也可以用于多类分类
作者：唐天泽
博客：http://write.blog.csdn.net/mdeditor#!postId=76188190
日期：2017-08-09
"""

# 导入本项目所需要的包
import pandas as pd
import numpy as np

from sklearn import datasets

from sklearn import svm

# 使用交叉验证的方法，把数据集分为训练集合测试集
from sklearn.model_selection import train_test_split

# The competition datafiles are in the directory ../input
# 加载数据集
def load_data():
    dataset = pd.read_csv("~/Desktop/knn/input/train.csv")
    label = dataset.values[:,0]
    train = dataset.values[:,1:]
    testdata  = pd.read_csv("~/Desktop/knn/input/test.csv").values
    return label,train,testdata
 # 使用LinearSVC考察线性分类SVM的预测能力
def test_LinearSVC(label,train,testdata):

    # 选择模型
    cls = svm.LinearSVC()

    # 把数据交给模型训练
    cls.fit(train,label)

    # 预测数据
    #print(cls.predict(testdata))
    results=cls.predict(testdata)
    return results

if __name__=="__main__":
    label,train,testdata = load_data()
    result = test_LinearSVC(label,train,testdata)
    pd.DataFrame({"ImageId": list(range(1,len(testdata)+1)),"Label": result}).to_csv(
    '~/Desktop/knn/output/Digit_recogniser_SVM_LinearSVC.csv', index=False,header=True)

8.参考资料

[1] 李航 《统计学习方法》
[2] 华校专《Python大战机器学习》