聚类模型-层次聚类
聚类模型
1、层次聚类
2、原型聚类-K-means
3、模型聚类-GMM
4、EM算法-LDA主题模型
5、密度聚类-DBSCAN
6、图聚类-谱聚类
一、层次聚类
一、聚类理论
一般来说,聚类是在训练样本的标签信息不知的情况下,学习样本内在的性质和规律,将有限的集合划分成 c c 类。根据“方以类聚,物以群分”的思想,类内对象尽可能的相似,类间对象尽可能不相似。因此,吾师言:聚类中两个关键的问题是:何为类?何为类内相似,类间不相似?以下所有的聚类模型皆从这两点出发。
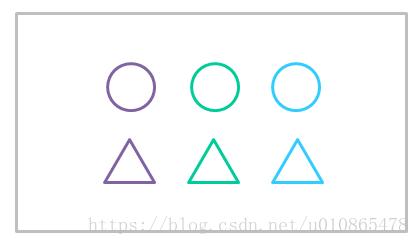
由于缺少样本标签,我们很难定义类和相似性,比如下面的问题:
按照颜色聚类可以分类三类,按照形状聚类可以分类两类,关键问题在于如何定义类,定义相似性。所以吾师还言:聚类一般不是一个任务的最终目标,而是一个预处理的过程。
聚类的评价指标有两种:
1)内部指标,指导思想是类内紧致性和类间分离性,比如Xie-Beni指标,DB指标
2)外部指标,假设数据集有标注,按有监督学习的评价指标进行评价
可以看出,外部指标有很大的问题,那就是聚类学到的数据规律不一定是标签,这对聚类算法的评价是不可靠的,但是对于只看结果,不评价模型的好坏是可以的,当然拿聚类的结果与有监督学习的结果对比是“无赖”的。
二、层次聚类
层次聚类的类表示可以看作是基于样本的, Xi X i 表示属于第 i i 的样本集合,即 Xi X i 作为第 i i 类的类表示。类相似性度量可以用“欧式距离”。层次聚类分为两种,一种是自底向上的凝聚层次聚类,一种是自顶向下的分裂层次聚类。两者的区别在于前者一开始将每一个样本看作一类,通过不断的合并最相似的两个簇,直到 c c 类;后者一开始将所有样本看作一类,通过最小化损失(类紧致)分裂为 c c 类。
凝聚层次聚类:
输入:样本数据 D=x1,x2,...,xm D = x 1 , x 2 , . . . , x m ,相似性度量函数 s s ,聚类簇数 k k
输出: k k 类样本
1)初始化每个样本为一个簇, ci=xi,i=1,2,...,m c i = x i , i = 1 , 2 , . . . , m
2)计算样本两两之间的距离 d(i,j),i=1,2...,m,j=1,2,...,m d ( i , j ) , i = 1 , 2... , m , j = 1 , 2 , . . . , m
3)通过相似性度量函数 s s ,找出最相似的两个簇进行合并
最小距离: s=dmin(ci,cj)=minx∈ci,z∈cjdist(x,z) s = d m i n ( c i , c j ) = min x ∈ c i , z ∈ c j d i s t ( x , z )
最大距离: s=dmax(ci,cj)=maxx∈ci,z∈cjdist(x,z) s = d m a x ( c i , c j ) = max x ∈ c i , z ∈ c j d i s t ( x , z )
平均距离: s=davg(ci,cj)=1|ci||cj|∑x∈ci∑z∈cjdist(x,z) s = d a v g ( c i , c j ) = 1 | c i | | c j | ∑ x ∈ c i ∑ z ∈ c j d i s t ( x , z )
4)直到簇数为 k k ,否则循环2)
分裂层次聚类:
输入:样本数据 D=x1,x2,...,xm D = x 1 , x 2 , . . . , x m ,损失函数 s s ,聚类簇数 k k
输出: k k 类样本
1)初始化所有样本为一个簇, c1={xi},i=1,2,...,m c 1 = { x i } , i = 1 , 2 , . . . , m
2)计算样本两两之间的距离 d(i,j),i=1,2...,m,j=1,2,...,m d ( i , j ) , i = 1 , 2... , m , j = 1 , 2 , . . . , m
3)计算当前所有簇 ci,i∈1,2..n<k c i , i ∈ 1 , 2.. n < k 的损失函数,选择损失最大的簇进行二分
计算该簇下两点间距离 d(i,j),i=1,2...,mi,j=1,2,...,mj d ( i , j ) , i = 1 , 2... , m i , j = 1 , 2 , . . . , m j ,选择簇中最远的两个点作为类中心将簇进行二分
4)直到簇数为 k k ,否则循环2)
值得注意的是分裂层次聚类在进行二分时,可以采用kmeans进行二分,这样时间复杂度就不再是 O(m2) O ( m 2 ) .
层次聚类算法特点:
1)可视化
2)采用计算样本两两之间的距离,时间复杂度为 O(m2) O ( m 2 )
3)凝聚和分裂的不可逆性