UVA - 1069 Always an integer （模拟）

Description

Combinatorics is a branch of mathematics chiefly concerned with counting discrete objects. For instance, how many ways can you pick two people out of a crowd ofn people? Into how many regions can you divide a circular disk by connectingn points on its boundary with one another? How many cubes are in a pyramid with square layers ranging from1×1 to n×n cubes?

Many questions like these have answers that can be reduced to simple polynomials inn. The answer to the first question above is n(n - 1)/2, or (n2 -n)/2. The answer to the second is (n4 - 6n3 + 23n2 - 18n + 24)/24. The answer to the third isn(n + 1)(2n + 1)/6, or (2n3 + 3n2 + n)/6. We write these polynomials in a standard form, as a polynomial with integer coefficients divided by a positive integer denominator.

These polynomials are answers to questions that can have integer answers only. But since they have fractional coefficients, they look as if they could produce non-integer results! Of course, evaluating these particular polynomials on a positive integer always results in an integer. For other polynomials of similar form, this is not necessarily true. It can be hard to tell the two cases apart. So that, naturally, is your task.

Input

The input consists of multiple test cases, each on a separate line. Each test case is an expression in the form(P)/D, where P is a polynomial with integer coefficients andD is a positive integer denominator. P is a sum of terms of the form CnE, where the coefficient C and the exponent E satisfy the following conditions:

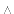1. E is an integer satisfying 0E100. If E is 0, then CnE is expressed as C. If E is 1, thenCn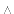E is expressed asCn, unless C is 1 or -1. In those instances,Cn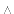E is expressed asn or - n.
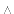2. C is an integer. If C is 1 or -1 andE is not 0 or 1, then the CnE will appear as n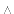E or- n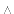E.
3. Only non-negative C values that are not part of the first term in the polynomial are preceded by +.
4. Exponents in consecutive terms are strictly decreasing.
5. C and D fit in a 32-bit signed integer.

See the sample input for details.

Input is terminated by a line containing a single period.

Output

For each test case, print the case number (starting with 1). Then print `Always an integer' if the test case polynomial evaluates to an integer for every positive integern. Print `Not always an integer' otherwise. Print the output for separate test cases on separate lines. Your output should follow the same format as the sample output.

Sample Input

(n^2-n)/2 
(2n^3+3n^2+n)/6 
(-n^14-11n+1)/3 
.

Sample Output

Case 1: Always an integer 
Case 2: Always an integer 
Case 3: Not always an integer
题意：给定一个形如P/D的多项式，判断它是否在所有正整数取到整数值
思路：刘汝佳入门经典的例题，分析太长，直接给结论吧：P（1）,P(2)..P(k+1)都是D的倍数，最后带入n检查就行了，n的范围是1-k+1

#include 
#include 
#include 
#include 
typedef long long ll;
using namespace std;
const int maxn = 110;

int c[maxn], e[maxn], p;
int tot, len, l, tmp;
char str[10001];
int flag;

ll pow_mod(ll a, ll p, ll n) {
	ll tmp = 1;
	while (p) {
		if (p & 1)
			tmp = (tmp * a) % n;
		p >>= 1;
		a = (a * a) % n;
	}
	return tmp;
}
void cal(int s, int a, int b) {
	int k, cs = 0, es = 0;
	for (k = a; k <= b; k++)
		if (str[k] == 'n')
			break;
	for (int i = a; i < k; i++)
		cs = cs * 10 + str[i] - '0';
	if (cs == 0)
		cs = s;
	else cs *= s;
	for (int i = k+2; i <= b; i++)
		es = es * 10 + str[i] - '0';
	if (k <= b && es == 0)
		es = 1;
	c[tot] = cs;
	e[tot++] = es;
}

int main() {
	int cas = 1;
	while (scanf("%s", str) && str[0] != '.') {
		len = strlen(str);
		l = tot = 0;
		if (str[1] == '-')
			l = 2;
		else l = 1;
		for (int i = l; i < len; i++) {
			if (str[i] == '+' || str[i] == '-' || str[i] == ')') {
				if (str[l-1] == '-')
					cal(-1, l, i-1);
				else cal(1, l, i-1);
				l = i+1;
			}
			if (str[i] == '/') {
				p = 0;
				for (int j = i+1; j < len; j++) 
					p = p*10 + str[j] - '0';
				break;	
			}
		}
		
		flag = 1;
		for (int i = 1; i < 200; i++) {
			tmp = 0;
			for (int j = 0; j < tot; j++)
					tmp = (tmp + (c[j]%p)*pow_mod(i, e[j], p)) % p;
			if (tmp) {
				flag = 0;
				break;
			}
		}

		if (flag) 
			printf("Case %d: Always an integer\n", cas++);
		else printf("Case %d: Not always an integer\n", cas++);
	}
	return 0;
}