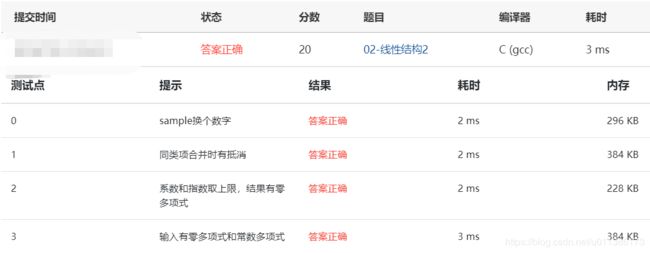
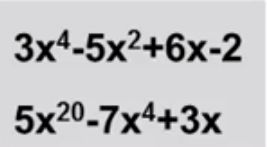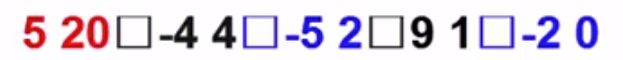02-线性结构2 一元多项式的乘法与加法运算

题目

设计函数分别求两个一元多项式的乘积与和。

输入格式:

输入分2行，每行分别先给出多项式非零项的个数，再以指数递降方式输入一个多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。

输出格式:

输出分2行，分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。零多项式应输出0 0。

输入样例:

4 3 4 -5 2  6 1  -2 0
3 5 20  -7 4  3 1

输出样例:

15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

要求

时间限制: 200 ms
内存限制: 64 MB
代码长度限制: 16 KB

题意理解

设计函数分别求两个一元多项式的乘积与和

已知两个多项式： （1） （2）

那么：

多项式和：

       多项式的乘积：

多项式乘积：

输入样例对应于两个多项式：

输出样例：

15 24 -25 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1 

两个多项式相乘的结果

5 20 -4 4 -5 2 9 1 -2 0 

两个多项式相加的结果

求解思路

1. 多项式表示
2. 程序框架
3. 读多项式
4. 加法实现
5. 乘法实现
6. 多项式输出

多项式的表示

仅表示非零项

  

一种比较好的实现方法：动态数组   (因为已经知道了有几个非零项）

下面介绍链表表示：

• 数据结构设计

typedef struct PolyNode *Polynomial;
struct PolyNode
{
    int coef; //系数
    int expon;//指数
    struct PolyNode *link; //指向下一个结点的指针
};

程序框架搭建

     ---> 

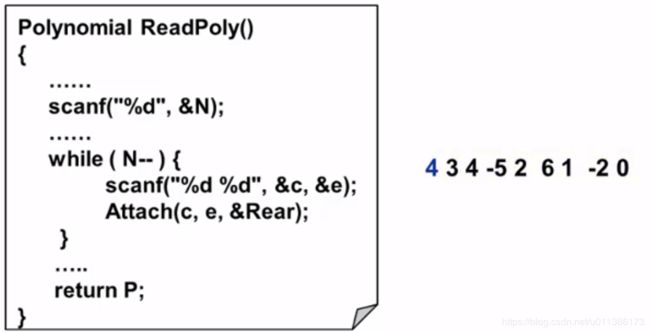
如何读入多项式

每次循环读入一对数，读入系数和指数后构造结点，插入多项式中；且因为是递降指数读入的，新的结点要插在上一个结点的后面）

最后形成:

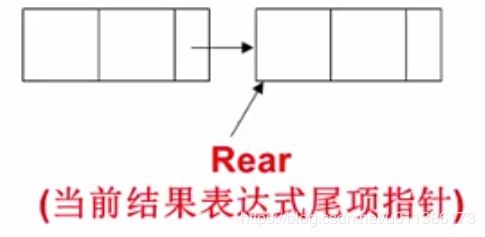
所以就需要一个指针Rear，指向链表的最后一个结点：

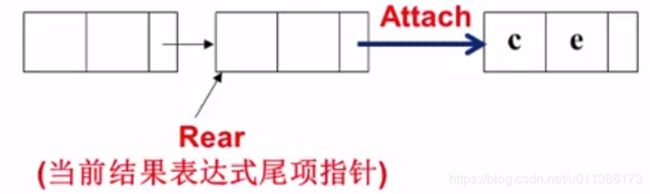
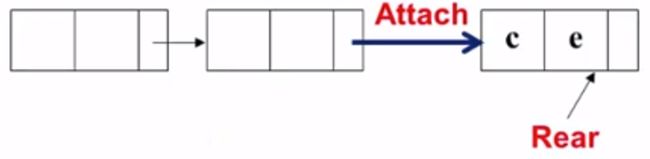
通过函数Attach，把新的结点插在当前链表的最后一个结点的后面：

将Rear指向新结点：

所以Rear在Attach函数中要被改变，而C语言中函数传递是值传递的，所以Rear要传入的是一个指针。

Rear初值是什么？两种处理方法：

1. Rear初值为NULL

     在Attach函数中根据Rear是否为NULL做不同处理。

     如果Rear为NULL，说明为刚开始的第一个结点，这个时候就要申请这个结点，将Rear指向这个结点；如果Rear不为NULL，直接将新的结点插入到Rear后面。

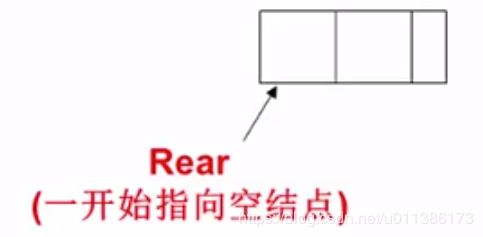
2. Rear指向一个空结点

 

以后所有新插入的结点都插在Rear后面。

如下是使Rear开始指向一个空结点的代码：

void Attach(int c, int e, Polynomial *pRear)
{
    Polynomial P;
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    P->coef = c; //对新结点赋值
    P->expon = e;
    P->link = NULL;
    (*pRear)->link = P;
    (*pRear) = P; //修改*pRear值
}

所以完整的读入多项式的代码：

Polynomial ReadPoly()
{
    Polynomial P, Rear, t;
    int c, e, N;
    scanf("%d", &N);
    P = (Polynomial)malloc(sizeof(struct PolyNode)); //构造链表头空结点
    P->link = NULL;
    Rear = P;
    while(N--)
    {
        scanf("%d %d", &c, &e);
        Attach(c, e, &Rear);   //将当前项插入多项式尾部
    }
    t = P;
    P = P->link;
    free(t);    //删除临时生成的头结点
    return P;
}

示意图：

经过上面的操作，P就会指向3,4这个结点，头结点被free掉。

如何将两个多项式相加

此前已经讲过，看下程序架构：

如何将两个多项式相乘

两种方法：

1. 将乘法运算转换为加法运算

将P1当前项乘P2多项式，再加到结果多项式里

t1 = P1;
t2 = P2;
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->link = NULL;
Rear = P;
while(t2)
{
    Attach(t1->coef * t2->coef, t1->expon + t2->expon, &Rear);
    t2 = t2->link;
}

2. 逐项插入

将P1当前项乘P2当前项，并插入到结果多项式中。关键是要找到插入位置。初始结果多项式可由P1第一项乘P2获得（如上）。

接下来讲讲逐项插入的做法：

（框架中有三个问题需要解释：1.如何构造初始多项式？2. 新的结点如何插入？ 3.结果如何处理，怎么返回？）

（1）如何构造初始多项式？

（2）新生成的结点如何插入？

（两重循环，t1的每一项乘以t2的没有项）

示意图：

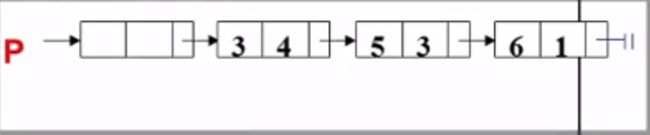
当前的计算结果由P1指示：

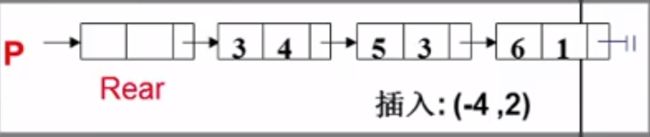
比较当前结点（Rear）的下一个结点的指数是否比要插入的结点指数大，如果大，Rear就往后挪：

当Rear指向5,3时，下一项的指数小于要插入的结点的指数，所以循环结束。

但是有可能下一项的指数与要插入的结点的指数相等，那么这种情况就要进行合并，系数相加。

具体细节：

系数加完之后是否为0：

如果指数不等，就要申请新的结点：

（3）结果如何处理？怎么返回？

要把开始构造的空结点删除。

即把P指向P的下一个结点（3,4），然后删除空结点。

如何将多项式输出

无论相加还是相乘，都得到了一个新的多项式。链表遍历的基本程序框架：

（flag控制空格的输出，最后一项后面没有空格输出。可以倒过来理解，第一项没有空格，其他每项输出格式都是：空格 系数 指数）

所以用flag来判断是否为第一项，如果flag = 0，则不输出空格，否则就要先输出空格，再输出系数和指数。

最后输出一个回车：

代码

#include 
#include 
 
typedef struct PolyNode *Polynominal;
struct PolyNode
{
    int coef;
    int expon;
    struct PolyNode *next;
};
 
void attach(int c, int e, Polynominal *rear)
{
    Polynominal p;
    p = (Polynominal)malloc(sizeof(struct PolyNode));
    p->coef = c;
    p->expon = e;
    p->next = NULL;
    (*rear)->next = p;
    (*rear) = p;
}
 
Polynominal readPoly()
{
    Polynominal p, rear;
    int n;
    int c;
    int e;
    scanf("%d", &n);
    p = (Polynominal)malloc(sizeof(struct PolyNode));
    p->next = NULL;
    rear = p;
    while(n--)
    {
        scanf("%d %d", &c, &e);
        attach(c, e, &rear); //形成一个链表
    }
    Polynominal temp = p;
    p = p->next;
    free(temp);
 
    return p;
}
 
int compare(int e1, int e2)
{
    if(e1 == e2) return 0;
    else if (e1 > e2) return 1;
    return -1;
}
 
Polynominal add(Polynominal p1, Polynominal p2)
{
    int sum;
    Polynominal rear = (Polynominal)malloc(sizeof(struct PolyNode));
    Polynominal front = rear;
    while(p1 && p2)
    {
        switch(compare(p1->expon, p2->expon))
        {
            case 1:
                attach(p1->coef, p1->expon, &rear);
                p1 = p1->next;
                break;
            case -1:
                attach(p2->coef, p2->expon, &rear);
                p2 = p2->next;
                break;
            case 0:
                sum = p1->coef + p2->coef;
                if (sum) //sum = 0则同类项合并时有抵消
                    attach(sum, p1->expon, &rear);
                p1 = p1->next;
                p2 = p2->next;
                break;
        }
    }
    while(p1)
    {
        attach(p1->coef, p1->expon, &rear);
        p1 = p1->next;
    }
 
    while(p2)
    {
        attach(p2->coef, p2->expon, &rear);
        p2 = p2->next;
    }
    rear->next = NULL;
    Polynominal temp = front;
    front = front->next;
    free(temp);
    return front;
}
 
Polynominal mult(Polynominal p1, Polynominal p2)
{
    if (!p1 || !p2)
        return NULL;
 
    int c, e;
    Polynominal p = (Polynominal)malloc(sizeof(struct PolyNode));
    Polynominal rear = p;
    Polynominal temp1 = p1;
    Polynominal temp2 = p2;
    Polynominal temp;
    while(temp2)  //p1的第一项乘p2，得到p
    {
        attach(temp1->coef * temp2->coef, temp1->expon + temp2->expon, &rear);
        temp2 = temp2->next;
    }
    temp1 = temp1->next;
    while(temp1)
    {
        temp2 = p2;
        rear = p;
        while(temp2)
        {
            e = temp1->expon + temp2->expon;
            c = temp1->coef * temp2->coef;
            while(rear->next && rear->next->expon > e)
                rear = rear->next;
            if (rear->next && rear->next->expon == e)
            {
                if (rear->next->coef + c)
                    rear->next->coef += c;
                else
                {
                    Polynominal temp = rear->next;
                    rear->next = temp->next;
                    free(temp);
                }
            }
            else
            {
                temp = (Polynominal)malloc(sizeof(struct PolyNode));
                temp->coef = c;
                temp->expon = e;
                temp->next = rear->next;
                rear->next = temp;
                rear = rear->next;
            }
            temp2 = temp2->next;
        }
        temp1 = temp1->next;
    }
    temp2 = p;
    p = p->next;
    free(temp2);
    return p;
}
 
void printPoly(Polynominal p)
{
    if (p == NULL)  //输入有零多项式和常数多项式
    {
        printf("0 0\n");
        return;
    }
 
    int flag = 0;
    while(p)
    {
        if(!flag)
            flag = 1;
        else
            printf(" ");
        printf("%d %d", p->coef, p->expon);
        p = p->next;
    }
    printf("\n");
}
 
int main()
{
    Polynominal p1 = readPoly();
    Polynominal p2 = readPoly();
    Polynominal pp = mult(p1, p2);
    printPoly(pp);
    Polynominal ps = add(p1, p2);
    printPoly(ps);
    return 0;
}

运行结果