中文信息处理 N-gram模型
一. 什么是建模?模型又是什么?
建模,是人们为了理解事物而对事物做出的一种抽象,是对事务进行书面无歧义的描述。
模型就是对实际问题或者是客观规律进行的形式化的表达。
二. 关于语言模型
长久以来,人们一直希望计算机可以理解我们人类的语言,从而进行一系列其他的应用,比如机器翻译,语音识别,分词,输入法,搜
索引擎的自动补全等。以前人们是进行基于规则的语言模型的研究方向,遇到了很大的问题,后来便出现了基于统计的语言模型,这些
在《数学之美》中吴军老师有进行详细的介绍。那么,当下人们使用最多,应用最广的便是n元语言模型。其实这个模型本质上就是在
判断一个句子是句子的概率.
三. N-gram model
1. 定义
假设一个句子是由 {w1,w2,w3,...wn} { w 1 , w 2 , w 3 , . . . w n } ,来表示的,其中 wi w i 表示的句子中的单词,那么,一个语言模型就可以用如下来表示:
P={w1,w2,w3,...wn} P = { w 1 , w 2 , w 3 , . . . w n }
那么我们将如何来计算呢?
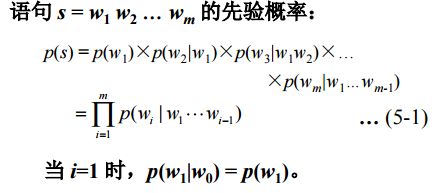
从公式可以看出,我们要计算这样一个表达式的,是非常困难的,于是,这个时候马尔可夫链便发挥了重大作用。
2.什么是马尔可夫链?
马尔科夫链描述的是一个随机状态,他指出某个状态只与其前(后)一个或者两个状态有关系,再往前的状态对当前状态的影响可以忽略不
算,这个整体还是比较符合人民的认知的。按照这个理论的话,上面的计算便可以简化,因为:
P{wm|w1,w2,...wn}=P{wm|wm−1,wm−2} P { w m | w 1 , w 2 , . . . w n } = P { w m | w m − 1 , w m − 2 }
以上就是一个简单的三阶马尔可夫链,也就是三元语言模型,属于二阶马尔科夫假设。
3.n-gram 模型应用举例
- 拼音转汉字
P(PinYin) = ta shi yan jiu sheng wu de
那么对应的可能的汉语是:
P(CString)ororor=他是研究生物的=踏实研究生物的=他实验救生物的=........ P ( C S t r i n g ) = 他 是 研 究 生 物 的 o r = 踏 实 研 究 生 物 的 o r = 他 实 验 救 生 物 的 o r = . . . . . . . .
那么究竟应该要翻译为哪一个句子才是对的,假设我们次用2元语言模型,其实就是在求每一个句子出现的概率。
P(CString1)=P(他|<BOS>)∗P(是|他)∗P(研究|是)∗P(生物|研究)∗P(的|生物)∗P(<EOS>|的) P ( C S t r i n g 1 ) = P ( 他 | < B O S > ) ∗ P ( 是 | 他 ) ∗ P ( 研 究 | 是 ) ∗ P ( 生 物 | 研 究 ) ∗ P ( 的 | 生 物 ) ∗ P ( < E O S > | 的 ) ;
P(CString2)=P(踏实|<BOS>)∗P(研究|踏实)∗P(生物|研究)∗P(的|生物)∗P(<EOS>|的) P ( C S t r i n g 2 ) = P ( 踏 实 | < B O S > ) ∗ P ( 研 究 | 踏 实 ) ∗ P ( 生 物 | 研 究 ) ∗ P ( 的 | 生 物 ) ∗ P ( < E O S > | 的 ) ;
………
- 中文分词
其实从上面就可以看出来,想要计算上面的表达式,首先就需要去进行中文分词。
那么假设已经分好词了,如何计算上面的表达式呢?
这里需要提及两个概念。
- 训练语料库 :training data. 用来训练模型的语料库。其实说简单点儿,就是比如人民日报啊,各种文献中的的句子的数据库罢了。
- 最大似然估计法:maximum like evaluation,MLE. 就是利用统计词频的办法来代替概率的计算。
4.参数估计
例如,给定训练语料:
“John read Moby Dick”,
“Mary read a different book”,
“She read a book by Cher”
根据 2 元文法求句子(She read a book.)的概率?
P(She|<BOS>)=c(<BOS>,She)∑wc(<BOS>,w)=13 P ( S h e | < B O S > ) = c ( < B O S > , S h e ) ∑ w c ( < B O S > , w ) = 1 3
P(read|She)=c(read,She)∑wc(She,w)=11=1 P ( r e a d | S h e ) = c ( r e a d , S h e ) ∑ w c ( S h e , w ) = 1 1 = 1
P(a|read>)=c(read,a)∑wc(read,w)=23 P ( a | r e a d > ) = c ( r e a d , a ) ∑ w c ( r e a d , w ) = 2 3
P(book|a>)=c(book,a)∑wc(a,w)=12 P ( b o o k | a > ) = c ( b o o k , a ) ∑ w c ( a , w ) = 1 2
P(<EOS>|book>)=c(book,<EOS>)∑wc(book,w)=12 P ( < E O S > | b o o k > ) = c ( b o o k , < E O S > ) ∑ w c ( b o o k , w ) = 1 2
P(She read a book) = 13∗1∗23∗23∗14=127 1 3 ∗ 1 ∗ 2 3 ∗ 2 3 ∗ 1 4 = 1 27
这样便解决了我们的问题。
但是考虑这样一个场景,假设我们想要分词的句子是:He read a book.
这样,由于He这个单词在语料库中从未出现过,导致句子概率为0,显然是不合理的。
这个问题的出现,主要是由于语料库数据稀少的原因,我们采用数据平滑的办法来解决。
关于数据平滑,我会在下一篇博客中继续分析整理,
乍一看好像内容有点儿少哈,刚刚看了一下关于MLE的推导过程,觉得还是蛮有趣的,有兴趣的同学可以去看看,在我第一篇的介绍中苏大老师课件上是有链接的。
这里,我主要对推导过程中用到的一些知识点进行整理:
- 拉格朗日乘数法
- 假设我们现在遇到的问题是,求解L=f(x,y,z)在约束条件 φ(x,y,z)=0 φ ( x , y , z ) = 0 下的极值,利用拉格朗日乘数法步骤如下:
假设拉格朗日乘子是 λ λ ,那么问题就会转换成下式的无约束条件函数求极值
L=f(x,y,z)+λφ(x,y,z) L = f ( x , y , z ) + λ φ ( x , y , z )
- 假设我们现在遇到的问题是,求解L=f(x,y,z)在约束条件 φ(x,y,z)=0 φ ( x , y , z ) = 0 下的极值,利用拉格朗日乘数法步骤如下:
- 对目标函数求对数在实际编程中也是很经常使用的技巧。好处有两点:
- 可以把乘法变成加法
- 可以让浮点数运算避免溢出。
- 取对数不会影响原目标函数求极值。

