[原创·论文阅读]Position tracking for virtual reality using commodity WiFi
这篇论文推出了一个叫WiCapture的系统。WiCapture系统的测试部署如图1所示。可以看到目标上有一个环形的天线,Oculus照相机用来做ground truth。
图1:WiCapture系统部署图
WiCapture系统可以实现对目标在空间中运动轨迹的追踪和绘制,追踪误差达到了0.88cm。
图2:WiCapture系统对运动目标轨迹的绘制
论文的主要思路是,发射机的位移δ和载波频率偏移(CFO)都会造成相位的偏移。因此,接收机收到的信号的相位偏移包含这两种因素。而由于CFO造成的偏移远大于发射机运动造成的偏移,因此必须消除CFO对相位偏移的影响。在消除CFO之后,得到的就只有因发射机位移而产生的相位变化。再通过求解残留的相位变化,可以得到位移δ。通过拼接每一段位移δ,最终可绘制出完整的运动轨迹。
为了实现上述思路,在不考虑CFO和发射机位移的情况下,我们首先对无线信道进行简单建模:
首先解释A矩阵的由来。假设空间中有L条多径,θk表示第k条多径对应的发射角。a(θk)表示对应第k条多径下,每一根天线发射信号的方向向量。
WiCapture运用了一个环形天线,以图3中第1根天线作为基准,第3根天线相对于它多运动的位移为d·cosθk。那么相应的相位差为e(-jπ*d*cosθk/λ)。同理,第2根天线相对于第1根天线的相位差也可得出。将L条多径下的向量全部组合起来,就得到了A矩阵。它描述的是在多径环境下,由发射角表示的方向向量的相位。
图3:第k条多径下的发射信号的方向向量
F矩阵是衰减矩阵,表征的是信号在无线环境的传输中经历的损耗,F矩阵中的每一个元素都是一个标量。那么,H=AF就得到了熟知的信道状态信息矩阵H,它描述了通信链路的信道属性。
现在,将由于发射机运动产生的相位偏差加入到模型中。发射机向接收机发包,典型间隔为10ms。在这么短的时间内,发射机的位移只有几毫米,因此,可以认为发射角在发P个包期间是相对不变的。发射机的位移造成的相位变化可以用下式表示:
图4:发射机的位移对路径传播的影响
发射机的运动未必一定会引起相位的改变。如图4,以AP为圆心,发射机与AP之间的距离为半径,当发射机沿着切向运动一小段位移时,相位是不会改变的,因为发射机与AP间距离未变。当发射机沿着径向运动时,会导致相位的改变,这个原理是显然的。rθk表示的是沿发射方向的单位向量,注意到发射机的运动对多径环境下的每一条径都有影响,把这种影响用D矩阵来表示。D矩阵是一个对角矩阵,除对角线外元素都是0.在收到第一个包时,发射机处于静止状态,因此H1=AF;在收到第二个包时,发射机运动了一段位移,因此H2=ADF。
图5:对角矩阵D的结构
现在将CFO的影响加入无线信道模型,
对第一个和第二个包,CFO造成的相位偏移分别为v1和v2,将观测到的CSI值命名为H1帽和H2帽,这样就完成了对整个模型的构建。下面考虑如何计算位移δ。
整体思路是,首先求解A矩阵中的向量,进而可以得到发射角θk ;然后求解观测到的衰减矩阵F;最后,使用衰减矩阵F和AoD共同估算位移δ。
求解A矩阵的一般方案是利用MUSIC算法,用第p个包的CSI来计算AoD。但一个包的误差可能是有很大波动的,因此在AoD基本不变的前提下,WiCapture利用多个包来估测AoD,具体做法是将多个包的CSI并联成一个更大的CSI矩阵,这样可以得到更为精确的AoD的值。
计算:由于H=AF,那么F=(A-)*H。但是A矩阵有逆矩阵是在A矩阵是方阵的前提下的。当A矩阵不是方阵时,使用A的伪逆矩阵来计算。可以理解为A的伪逆矩阵具有与A的逆矩阵类似的作用。
于是可以计算出F1和F2的值,然后使用下面的公式计算D矩阵:
现在,计算出的D矩阵,其第k个对角线上的元素为
这与我们的估计是有出入的,因为还没有消除CFO的偏差。WiCapture使用了一种独特的方法来消除CFO,即使用了多径中信号的相位信息。因为对每一径,CFO对它的影响是相同的,可以通过对不同径的相位做相减操作来抵消。具体方法如下:通过下列方程来求解δ,
s向量的第k个元素是Dk+1,k+1/D1,1,它的值是,
可以发现v2-v1这一项已经被抵消了,也就是说CFO的影响被消除了。
再来看R矩阵的结构,
图6:R矩阵的结构
因此,R·δ和s向量理论上是相等的,它们是从不同的角度计算的--R矩阵是利用第一步得到的AoD计算的,s向量是利用衰减矩阵F计算的。求解的δ值,恰好可使这两项相等。在得到每一个δ后,可以把它们拼接起来,形成一段完整的轨迹。
上述的分析是针对单AP而言的。WiCapture是基于多AP工作的,多AP的情形下,发射机进行了一段位移,每一个AP都收到了CSI包,根据这些CSI包,可以计算出各自的AoD和F矩阵,那么可形成各自的R矩阵和s向量。把这些R矩阵和s向量分别并联起来,最终能计算出更为精确的δ值。
![[原创·论文阅读]Position tracking for virtual reality using commodity WiFi_第1张图片](http://img.e-com-net.com/image/info8/8a28684c85dd4dab9da0e453f0a8af78.jpg)
![[原创·论文阅读]Position tracking for virtual reality using commodity WiFi_第2张图片](http://img.e-com-net.com/image/info8/e123ba97849c49d3a552b93873e34999.jpg)
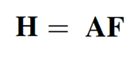
![[原创·论文阅读]Position tracking for virtual reality using commodity WiFi_第3张图片](http://img.e-com-net.com/image/info8/214f64a45bbb4adca9c2ccc5754fb7cb.jpg)
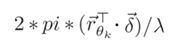
![[原创·论文阅读]Position tracking for virtual reality using commodity WiFi_第4张图片](http://img.e-com-net.com/image/info8/68adec7c46ef4da5a07aec25fd8052cc.jpg)
![[原创·论文阅读]Position tracking for virtual reality using commodity WiFi_第5张图片](http://img.e-com-net.com/image/info8/45ec44b325134554b6dd508d4b3fee06.jpg)
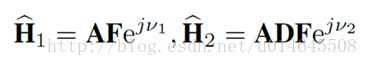

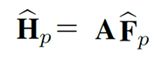
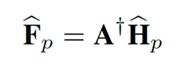
![[原创·论文阅读]Position tracking for virtual reality using commodity WiFi_第6张图片](http://img.e-com-net.com/image/info8/65d16f4c093f4931a2bbe2df857a64df.jpg)
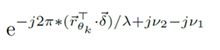
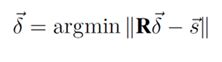
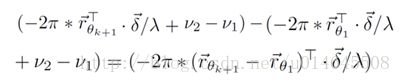
![[原创·论文阅读]Position tracking for virtual reality using commodity WiFi_第7张图片](http://img.e-com-net.com/image/info8/728933526d9244f789523f2f1d93bf79.jpg)