还不懂排序算法可以打我了!
排序算法
- 0. 前言
- 1. 冒泡算法
- 2. 插入算法
- 3. 希尔排序
- 4. 归并排序
- 5. 快速排序
- 6. 堆排序
- 7. 基数排序
- 8. 总结
0. 前言
评价一个算法的好坏,除了其是否具有较低的时间复杂度之外,还有其稳定性以及空间复杂度。
稳定性的判断标注是数组元素的值相同时,进行元素交换后,相对位置如果发生变化,变化则不具有稳定性。
1. 冒泡算法
冒泡排序可以说是每个程序员接触到的第一个排序算法,其算法思想较为简单。
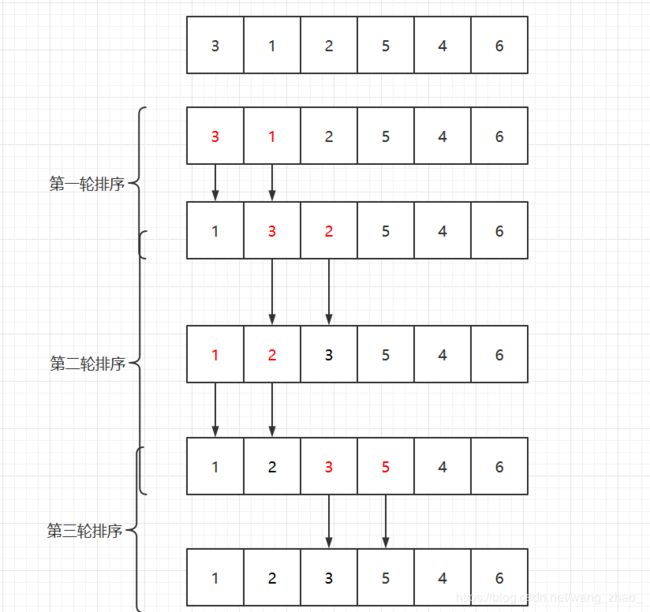
在每一轮的排序中,对待排序子数组中的相邻元素进行比较,如果逆序,则交换位置。当一轮结束后,待排序子数组中最大的元素便出现了子数组最后一个位置。
具体如下图所示:
package sort;
import java.util.Arrays;
/**
* @author wangzhao
* @date 2020/6/15 20:48
*/
public class BubbleSort {
public static void sort(int[] array){
if (array == null){
return;
}
for (int i = 0; i <array.length; i++){
// 不断缩小子数组的范围
for (int j = 1; j < array.length - i; j++){
// 如果逆序,则交换位置
if (array[j] < array[j - 1]){
swap(array, j, j-1);
}
}
}
}
private static void swap(int[] array, int j, int i) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
一个长度为n的数组,上述代码需要进行n-1趟的排序。但是我们可以看上图,在第一趟排序后,整个数字便完全有序了,无需进行后续操作。
所以上述代码可进行优化,优化后的代码如下:
public static void sort(int[] array){
if (array == null){
return;
}
for (int i = 0; i <array.length; i++){
// flag 用于标识该趟有没有进行元素交换,没有交换的话,则说明已经完全没有了
boolean flag = false;
for (int j = 1; j < array.length - i; j++){
flag = true;
if (array[j] < array[j - 1]){
swap(array, j, j-1);
}
}
if(!flag){
break;
}
}
}
接下来分析冒泡算法的效率。
时间复杂度O(n)=(n^2),最坏的情况下,数组为一个完全逆序的数组,此时不管是否优化,依然需要O(n)=(n^2),如果是一个有序的数组,那么在优化后的代码,只需要O(n)=(n)。
空间复杂度O(1),因为我们只引用到了固定的常量而已。
稳定性:稳定。
2. 插入算法
插入排序有点像我们打扑克牌时,把小的牌插入到左边,以此达到这个牌有序。
将每一个元素插入到其他已经有序的元素中的适当位置。当前索引左边的元素都是有序的,但他们的最终位置还不确定,为了给更小的元素腾出空间,它们可能会向右移动。
package sort;
import java.util.Arrays;
/**
* @author wangzhao
* @date 2020/6/15 21:24
*/
public class InsertSort {
public static void sort(int[] array){
if (array == null){
return;
}
for(int i = 1; i < array.length; i++){
for (int j = i; j > 0 && array[j] < array[j-1]; j--){
swap(array, j, j-1);
}
}
}
private static void swap(int[] array, int j, int i) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
接下来分析插入算法的效率。
时间复杂度O(n)=(n^2),最坏的情况下,数组为一个完全逆序的数组,需要O(n)=(n^2),如果是一个有序的数组,只需要O(n)=(n)。
空间复杂度O(1),因为我们只引用到了固定的常量而已。
稳定性:稳定。
3. 希尔排序
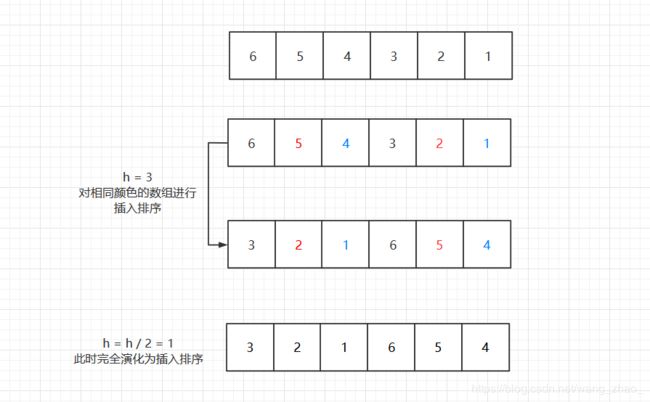
对于插入排序来说,它只会交换相邻的元素,因此它只能一点一点地从数组地一端移动到另一端,如果最小元素在最右边,需要n-1次交换才能移动最左端。
希尔排序算法思想:使数组中任意间隔为h的元素都是有序地,这样的数组称为h有序数组。然后不断缩小h的值,直到h为1,此时可看作是插入排序。相比于插入排序,这样可以上述的极端情况下,更快的将元素交换到它的正确位置。
package sort;
import java.util.Arrays;
/**
* @author wangzhao
* @date 2020/6/15 21:46
*/
public class ShellSort {
public static void sort(int[] array){
if (array == null){
return;
}
// 通常 h 并不是如此计算,有更好的方法,这里只说明算法思想,暂如此采用
int h = array.length / 2;
while (h >= 1){
for (int i = h; i < array.length; i++){
for (int j = i; j > h && array[j] < array[j-h]; j -= h){
swap(array, j, j-h);
}
}
// 不断缩小 h 的值,直到为 1
h /= 2;
}
}
}
接下来分析希尔算法的效率。
时间复杂度O(n^(1.3—2)),最后h会退化到1,但如果前期的排序中,能够将小元素直接放到前面,一定程度上可以较低时间复杂的。
空间复杂度O(1),因为我们只引用到了固定的常量而已。
稳定性:不稳定。
4. 归并排序
算法思想:要将一个数组排序,可以先(递归地)将它分成两半分别排序,然后将结果归并起来。
既然递归,则一定存在递归的终止条件,终止条件为只存在一个元素,如何判断只存在一个元素,左右下标相等。
接着是进行合并,合并则是对两个有序数组进行合并,借助一个辅助数组很容易实现。
package sort;
import java.util.Arrays;
/**
* @author wangzhao
* @date 2020/6/15 22:13
*/
public class MergeSort {
// 辅助数组
private static int[] aux_array = null;
public static void sort(int[] array){
if (array == null){
return;
}
aux_array = new int[array.length];
int left = 0;
int right = array.length - 1;
recursive(array, left, right);
}
public static void recursive(int[] array, int left, int right){
// 只存在一个元素,递归结束
if (left == right)
return;
int mid = ((left - right) >> 1) + right;
recursive(array, left, mid);
recursive(array, mid+1, right);
merge(array, left, mid, right);
}
private static void merge(int[] array, int left, int mid, int right) {
int index = left;
int i, j = 0;
for (i = left, j = mid + 1; i <= mid && j <= right;){
if(array[i] < array[j]){
aux_array[index++] = array[i++];
}else{
aux_array[index++] = array[j++];
}
}
while (i <= mid){
aux_array[index++] = array[i++];
}
while (j <= right) {
aux_array[index++] = array[j++];
}
// 此时,辅助数组已经将子数组合并完成,将辅助数组中的元素拷贝回原数组中
for (index = left; index <= right; index++){
array[index] = aux_array[index];
}
}
}
接下来分析归并算法的效率。
时间复杂度O(nlog(n))。
空间复杂度O(n),有相关论文表示可以做到O(1),如感兴趣,可自行查阅。
稳定性:稳定。
5. 快速排序
算法思想:每次在数组中,选择一个哨兵,比哨兵大的元素放到其右边,小的则放到其左边,这样每一次就将哨兵的元素给排好了,然后对哨兵左右的子数组进行递归上述操作。
将大于哨兵的元素放到其右边,小于哨兵的放到其左边,并且返回哨兵的下标可以才用如下算法:
将数组划分为两个区域,分别为大于和小于等于的区域,具体代码如下:
public static int partition(int[] array, int left, int right){
// 将数组划分为两部分,low 区为小于等于哨兵array[right]的区域,high 区为大于哨兵array[right]的区域
int low = left - 1;
int high = right;
for(int i = left; i < high; i++){
if(array[i] <= array[right]){
// low 区扩大
swap(array, i, ++low);
}else{
// high 区扩大
swap(array, i, --high);
// 注意,这里要进行 i--,因为换来的元素不知道其大小
i--;
}
}
// 最后,将哨兵放到其正确的位置
swap(array, right, high);
return high;
}
完整代码如下:
package sort;
import java.util.Arrays;
/**
* @author wangzhao
* @date 2020/6/15 23:14
*/
public class QuickSort {
public static void sort(int[] array){
if (array == null){
return;
}
int left = 0;
int right = array.length - 1;
quickSort(array, left, right);
}
public static void quickSort(int[] array, int left, int right){
if (right == left || right <= 0 || left >= array.length - 1)
return;
int index = partition(array, left, right);
quickSort(array, left, index-1);
quickSort(array, index + 1, right);
}
public static int partition(int[] array, int left, int right){
// 将数组划分为两部分,low 区为小于等于哨兵array[right]的区域,high 区为大于哨兵array[right]的区域
int low = left - 1;
int high = right;
for(int i = left; i < high; i++){
if(array[i] <= array[right]){
// low 区扩大
swap(array, i, ++low);
}else{
// high 区扩大
swap(array, i, --high);
// 注意,这里要进行 i--,因为换来的元素不知道其大小
i--;
}
}
// 最后,将哨兵放到其正确的位置
swap(array, right, high);
return high;
}
}
快排优化,在上面的代码中,我们每次只能返回一个下标。将数组划分为3块,小于目标值区域,等于目标值区域,大于目标值区域。
这样当出现相同的元素时,每次返回相等元素的左右边界,这样可以对子数组的划分变小,同时也可以避免无意义的排序。
// 三向切分
private static int[] partition_2(int[] array, int left, int right) {
int lower = left-1; // 小于目标值的区域
int high = right; // 大于等于目标值的区域
for(int i = left; i < high; i++){
if (array[i] < array[right]){
swap(array, i, ++lower);
}else if (array[i] > array[right]){
swap(array, i, --high);
i--;
}else{
continue;
}
}
swap (array, high, right);
return new int[]{lower,high+1};
}
接下来分析快排算法的效率。
时间复杂度O(n)=(nlog(n))。
空间复杂度O(1),因为我们只引用到了固定的常量而已。
稳定性:不稳定。
6. 堆排序
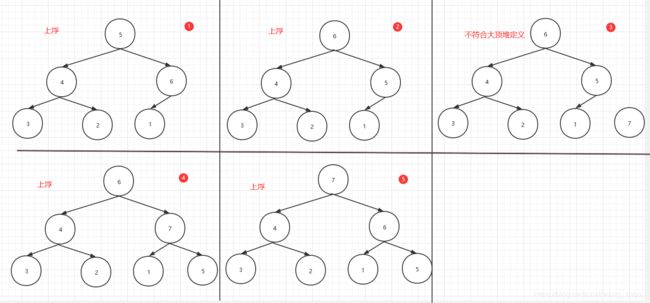
我们首先介绍一下大顶堆,大顶堆指堆顶的元素大于等于其左右儿子节点的元素,小顶堆则相反。
如下图,所示一个大顶堆。

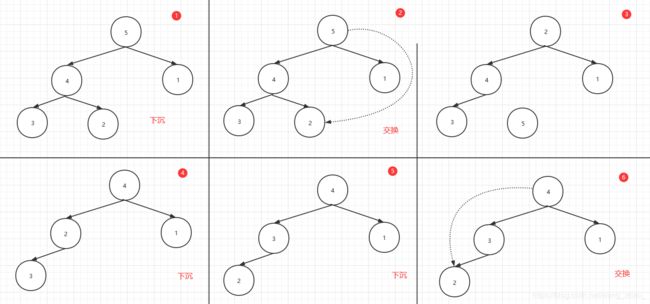
[5, 4, 1, 3, 2, 6, 7]形成大顶堆的形成过程如下:
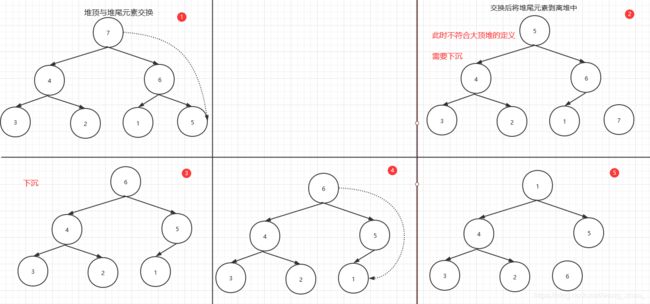
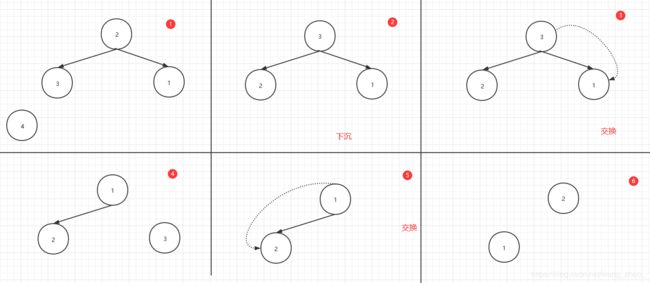
堆排序的思路则是将堆顶元素与最后一个元素进行交换,此时堆中的最后一个元素,便是数组最大的元素。交换后,由于不符合大顶堆的定义,所以我们需要对堆进行调整,使之保持大顶堆的形态。
现在我们倒着看每次从堆尾剥离的元素,可以发现其是一个递增的有序序列。
整个堆排序涉及两个操作,上浮及下沉。
上浮
当某个节点的大于其父节点(或是在堆底加入了一个新的元素)时,我们需要由下而上恢复堆的顺序。
如果当前节点比其父节点大,则交换,直到我们遇到更大的父节点。
/**
*
* @param array 可以视作堆
* @param insertIndex 堆中待插入的下标,需要注意的是,这里的下标并不是数组最后一个下标,堆中每次插入一个元素后,insertIndex + 1
* @param target 待插入元素
*/
public static void swim(int[] array, int insertIndex, int target){
// 将元素插入堆中
array[insertIndex] = target;
// 判断是否符合大顶堆
while (insertIndex > 0 && array[insertIndex] > array[insertIndex/2]){
swap(array, insertIndex, insertIndex/2);
insertIndex /= 2;
}
}
下沉
当某个节点的小于其子节点(例如将根节点替换为一个较小的元素)时,我们需要由上而下恢复堆的顺序。
如果某个节点变得比它的两个子节点或是其中之一更小了,那么我们可以通过将它和它的两个子节点中的较大者交换,直到没有比它更大的子节点或者到达底部为止。
/**
*
* @param array 可以视作堆
* @param index 需要下沉节点的下标,如果是堆排序,则其默认为 0
* @param heapLastIndex 堆中最后一个元素的下标,需要注意的是,这里的下标并不是数组最后一个下标,每次移除堆尾的元素,heapLastIndex - 1
*/
public static void sink(int[] array,int index, int heapLastIndex){
// 不能超过堆中最后一个元素
while (index * 2 < heapLastIndex){
int leftIndex = 2 * index + 1;
int rightIndex = 2 * index + 2;
// 该变量用来记录两个节点中较大的下标
int maxIndex = leftIndex;
// 此时,说明一定存在两个儿子节点
if (rightIndex <= heapLastIndex){
maxIndex = array[leftIndex] > array[rightIndex] ? leftIndex : rightIndex;
}
// 如果父节点,大于最大的儿子节点,符合大顶堆,退出
if (array[index] > array[maxIndex]){
break;
}
swap(array, index, maxIndex);
index = maxIndex;
}
}
完整代码:
package sort;
import java.util.Arrays;
/**
* @author wangzhao
* @date 2020/6/16 1:08
*/
public class HeapSort {
public static void sort(int[] array){
if (array == null){
return;
}
// 生成大顶堆
for (int i=0; i < array.length; i++){
swim(array, i, array[i]);
}
for (int i=array.length - 1; i > 0; i--){
swap(array, 0, i);
sink(array, 0, i-1);
}
}
/**
*
* @param array 可以视作堆
* @param insertIndex 堆中待插入的下标,需要注意的是,这里的下标并不是数组最后一个下标,堆中每次插入一个元素后,insertIndex + 1
* @param target 待插入元素
*/
public static void swim(int[] array, int insertIndex, int target){
// 将元素插入堆中
array[insertIndex] = target;
// 判断是否符合大顶堆
while (insertIndex > 0 && array[insertIndex] > array[insertIndex/2]){
swap(array, insertIndex, insertIndex/2);
insertIndex /= 2;
}
}
/**
*
* @param array 可以视作堆
* @param index 需要下沉节点的下标,如果是堆排序,则其默认为 0
* @param heapLastIndex 堆中最后一个元素的下标,需要注意的是,这里的下标并不是数组最后一个下标,每次移除堆尾的元素,heapLastIndex - 1
*/
public static void sink(int[] array,int index, int heapLastIndex){
// 不能超过堆中最后一个元素
while (index * 2 < heapLastIndex){
int leftIndex = 2 * index + 1;
int rightIndex = 2 * index + 2;
// 该变量用来记录两个节点中较大的下标
int maxIndex = leftIndex;
// 此时,说明一定存在两个儿子节点
if (rightIndex <= heapLastIndex){
maxIndex = array[leftIndex] > array[rightIndex] ? leftIndex : rightIndex;
}
// 如果父节点,大于最大的儿子节点,符合大顶堆,退出
if (array[index] > array[maxIndex]){
break;
}
swap(array, index, maxIndex);
index = maxIndex;
}
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
接下来分析堆排序的效率。
时间复杂度O(n)=(nlog(n))。
空间复杂度O(1),因为我们只引用到了固定的常量而已。
稳定性:不稳定。
7. 基数排序
基数排序可以参考之前写的一篇博客。基数排序
8. 总结
至此,所有的主流排序算法都已介绍加Coding完成,有很多有意思还未介绍的地方。如堆排序中可以被扩展到的优先队列,这个挺有趣,面试中可能会有这样一个问题,如何在100万的数字中,选择最大or最小的10个数。
虽然上面既有时间复杂度为O(n^2),也有O(nlong)复杂度的排序算法,但并不意味着时间复杂度越低,表现就越优秀,还和其数据量相同。
对于工程排序,往往是采用多种排序算法的结合,这里我们以Arrays.sort为例,观察其代码:
static void sort(int[] a, int left, int right,
int[] work, int workBase, int workLen) {
// Use Quicksort on small arrays
if (right - left < QUICKSORT_THRESHOLD) {
sort(a, left, right, true);
return;
}
/*
* Index run[i] is the start of i-th run
* (ascending or descending sequence).
*/
int[] run = new int[MAX_RUN_COUNT + 1];
int count = 0; run[0] = left;
// Check if the array is nearly sorted
for (int k = left; k < right; run[count] = k) {
if (a[k] < a[k + 1]) { // ascending
while (++k <= right && a[k - 1] <= a[k]);
} else if (a[k] > a[k + 1]) { // descending
while (++k <= right && a[k - 1] >= a[k]);
for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {
int t = a[lo]; a[lo] = a[hi]; a[hi] = t;
}
} else { // equal
for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) {
if (--m == 0) {
sort(a, left, right, true);
return;
}
}
}
/*
* The array is not highly structured,
* use Quicksort instead of merge sort.
*/
if (++count == MAX_RUN_COUNT) {
sort(a, left, right, true);
return;
}
}
// Check special cases
// Implementation note: variable "right" is increased by 1.
if (run[count] == right++) { // The last run contains one element
run[++count] = right;
} else if (count == 1) { // The array is already sorted
return;
}
// Determine alternation base for merge
byte odd = 0;
for (int n = 1; (n <<= 1) < count; odd ^= 1);
// Use or create temporary array b for merging
int[] b; // temp array; alternates with a
int ao, bo; // array offsets from 'left'
int blen = right - left; // space needed for b
if (work == null || workLen < blen || workBase + blen > work.length) {
work = new int[blen];
workBase = 0;
}
if (odd == 0) {
System.arraycopy(a, left, work, workBase, blen);
b = a;
bo = 0;
a = work;
ao = workBase - left;
} else {
b = work;
ao = 0;
bo = workBase - left;
}
// Merging
for (int last; count > 1; count = last) {
for (int k = (last = 0) + 2; k <= count; k += 2) {
int hi = run[k], mi = run[k - 1];
for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {
if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {
b[i + bo] = a[p++ + ao];
} else {
b[i + bo] = a[q++ + ao];
}
}
run[++last] = hi;
}
if ((count & 1) != 0) {
for (int i = right, lo = run[count - 1]; --i >= lo;
b[i + bo] = a[i + ao]
);
run[++last] = right;
}
int[] t = a; a = b; b = t;
int o = ao; ao = bo; bo = o;
}
}
根据数据量的多少,采用了插入排序,快速排序,归并排序三种排序的组合。