KMP算法复习【+继续学习】

离NOIP还剩12天，本蒟蒻开始准备复习了。

先来个KMP【似乎我并没有写过KMP的blog】

KMP

KMP算法是解决字符串匹配问题的一个算法，主要是单对单的字符串匹配加速，时间复杂度O(m + n)

KMP算法主要是基于fail[]数组，fail[j]数组的含义就是，对于模式串P[]，当j号位匹配失败时，应该跳向前面哪一位继续比较

想象我们日常比较字符串，对于abcdaabcx这个字符串我们与另外一个字符串比较，我们前面几个都顺风顺水地匹配了，当我们到达x这个字符时，发现并不匹配【真是令人失望】，那么前面的比较岂不白费了？

这个时候按照常规的思路我们将模式串向后移一位继续与匹配串从头开始比较，但我们前面是比较过了的啊，重新比较就很浪费时间了。

我们考虑从哪里开始比较最为合适，如果能找到一个最长的前缀使之与当前后缀匹配，那移动过来后，前缀部分一定是匹配的，我们只需从该前缀下一位继续比较即可

如何构造？看代码吧：

void getf(){
	int j = f[0] = -1,i = 0;
	while (i < n){
		while (j != -1 && P[j] != P[i]) j = f[j];
		f[++i] = ++j;
	}
}

构造fail数组的过程实际上就是模式串P自我匹配的过程

比较函数也是类似的：

void KMP(){
	int j = 0;
	for (int i = 0; i < m; i++){
		while (j != -1 && P[j] != T[i]) j = f[j];
		j++;
		if (j == n){
			//统计答案
			j = f[j];
		}
	}
}

做三道练习：

模板题POJ3461

充分理解fail数组:POJ2752

    这道题要找出所有前缀 = 后缀，构造出fail数组就可以找到了，要注意字符串本身也可以作为前后缀

fail数组的理解:POJ2406

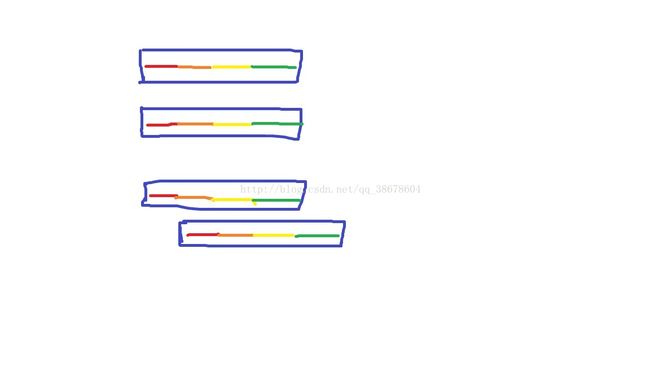
     求字符串的最小周期数，如果(n - f[n]) | n，如下图

首先自身与自身一定匹配，若错开一定位置仍匹配，就会出现如图的连锁匹配，致使全字符串分成相等的几分

这就是fail函数呈现出来的周期性

好了今天就复习这么多KMP【还是很弱】

转载于:https://www.cnblogs.com/Mychael/p/8282842.html