从零开始_学_数据结构(零)——数据结构总述
参考文献:《大话数据结构》作者:程杰
写在最开始:
这是我自己学习的经验和记录,有的内容很容易理解,但又比较重要,我会直接摘抄书上的内容;有些比较复杂,我会写明自己的思考;有些我自己也没搞懂,我会用红色文字标明,写出自己的疑问,也许以后会解决。
数据结构的概念:
是一门研究非数值计算的程序设计问题中的操作对象,以及它们之间的关系和操作等相关问题的学科。
注:这句话应该意思是,数据结构不是研究数值和数值计算的,而是研究对象(对象不止是数值,也可能是类对象或者其他),研究这些对象之间的关系(比如有什么共同点,比如顺序如何),以及操作(比如排序,插入等)。
数据结构的基础:
数据
数据的概念:
概括的来说数据,就是一切有意义的符号(我觉得可以说是数值)。例如,整型是数值是他自己(但存储形式是通过二进制内容),图像(最简单的是NTFS文件系统中的BitMap表,用一位(0或1,8位是1字节)来表示某一个簇是否被使用(1表示已使用,0相反)),声音(这个不太清楚)等。
由于一切数据都是以二进制数值的形式存储在硬盘或者内存的,因为可以认为这些二进制数值就是数据,但我个人认为,如果二进制数值没有意义的话,那么也不能称为数据(因为他不表示任何内容)。
并且,计算机的数据,要能被输入到计算机中(不止是PC),也要能被处理(没意义是不能被处理的,损坏的也不行)。
数据元素:
是组成数据、有一定意义的基本单位,在计算机中通常作为整体处理,也被称为记录。
例如,一个二进制位,如果我们要强行理解的话,只能以bool类型来理解,但若我们需要的是int类型的数据(4字节),那么显然是最小单位需要是4字节(32位)了,因为只有这样,这个int类型的数值也有意义。
因此,所谓的数据元素,就是指数据的一个单元,具体这个单元有多大,要根据实际需求而定。
数据项:
假如要分析结构数组,那么数据元素是结构,而结构是由若干个类型的变量组成,而这些变量,就是数据项。
数据项是数据不可分割的最小单位。(这样将其定义,再小的话不一定有意义)
数据对象:
是性质相同的数据元素的集合,是数据的子集,一般简称为数据。
例如数据有int类型,有结构,有类,毫无疑问,他们都是数据。
但假如我们只分析结构,那么其他数据对我们来说就没意义,也没必要去处理。
而对我们有意义的结构,则是我们的研究对象——数据对象,对我们来说,他们就是数据(全部数据的一部分,,是我们研究内容的全部)。
数据结构:
数据结构,是相互之间存在一种或者多种特定关系的数据元素的集合。
也就是说,某些数据之间,是存在一定联系的。例如数组,数组元素之间的联系就是同属于一个数组。
也许还有其他的关系,书上后面可能会讲(我大概看了眼后面的)。反正肯定有关系。
逻辑结构:
指数据对象中,数据元素之间的关系。
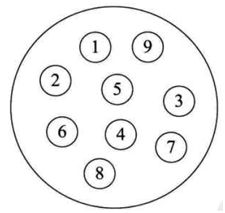
(1)集合结构
数据对象中的所有数据元素,他们之间的关系是:同属于一个集合。
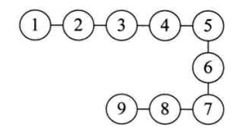
(2)线性结构
数据元素之间的关系,是一对一的关系。
例如链表,前一个节点有指针指向后一个节点。
(3)树形结构
数据元素之间的关系,存在一对多的层次关系。
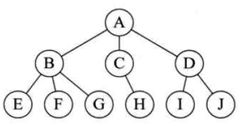
注意,是 分层的,从上往下是一对多。
如图,A的第一层,BCD是第二层,其他是第三层。从上层往下层对应,上层的并不同时对应下层的某一个节点,这样才能理解为一对多。
(4)图形结构
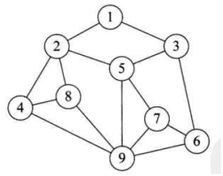
其中数据元素的关系是多对多。
如图,1对应2和3,然后2和3又共同对应5,分别对应4、8、6。
个人觉得树和图形结构的最大区别,是树是分层的,而图并不分层。
但这个想法尚未验证。
画逻辑结构时:
①每个圆圈是一个节点,可以用一个空园表示空节点;(至少可以表示空树)
②元素之间的逻辑关系,用节点之间的连线表示,如果这个关系是有方向的,用带箭头的连线(不能理解,什么叫做元素之间的逻辑关系?什么又叫做有方向的?)
逻辑结构的用处:
逻辑结构是针对具体问题的,是为了解决问题而定义的。
例如,一个树形结构的数据对象,也可以将其理解为集合(因为也可以属于同一个集合),至于同时存在图和树或者其他的关系,暂时不能理解。
也许是一个结构同时具有树形的指针,也具有线性的指针就可以做到同时具备两种数据结构?
物理结构:
指数据的逻辑结构,在计算机中的存储形式。
补充:指在内存。若是在硬盘或者之类的地方,称为文件结构。
例如,一个1GB的文件,你要在里面找到Student对象A和Student对象B。
设定为你先找到了对象A(比如A在文件中的地址是第一个字节)。
(1)假如B存储在A之后的位置,那么如果使用逐字节方式的话,你会立刻找到B。
(2)假如B存储在A之后很远的位置,如果逐字节去找,那么会需要很久时间。
(3)假如有一个指针,他和A在一起,你找到A后,可以同时获得指针A的值,而假如指针A指向B,那么就知道了对象B的地址。因此,便立刻找到了对象B(即使B实际地址和A的距离很远)。
这种思想,在学C++的单向链表的时候是使用过的。
对于(1)的情况,这种存储形式叫做 顺序存储。
对于(3)的情况,这种存储形式叫做 链式存储。
链式存储的优点:
当需要插入新元素时,可以方便的插入,只需要更改前一个元素的指针即可(如果是双向链表,也需要更改后一个元素的指针),删除也同理。
链式存储的缺点:
需要占用更多的内存(因为要有一个或多个指针,用于指向下一个对象);
假如中间有一个节点损坏,那么无法找到下一个节点(没有下一个节点的地址)。
顺序存储的优点:
正好和链式存储相反,节约内存。假如对象是char字符(1字节),一个指针也占一字节,因此链式存储一个节点需要的内存比顺序存储多了一倍。
不会丢失数据,即使中间有节点出问题,也可以通过读取下一个地址来知道下一个元素的值。
顺序存储的缺点:
插入、删除都很不方便,很容易导致效率低下。
抽象数据类型:
数据类型:书上的定义很拗口,反正像int、char、结构、自定义类这样的就是数据类型。
抽象数据类型:就是指我们把某些信息抽象为什么样类型,例如“人名+学号+成绩+班级=学生”。这个“学生类”就是一个抽象数据类型,他包含人名(可能是string类),学号(可能是int类),成绩(可能是short类),班级(可能是char类)。
抽象包括了两个特点:①一个数学模型;②定义在模型的一组操作。
而在上面“学生类”的基础上,单纯只有数据是没有意义的。
例如,我们需要知道学生的成绩,因此,应该有一个显示学生成绩的方法(类方法);
例如,我们可能需要更改其分数(或者创建该对象时添加一个分数),因此,需要一个初始化学生成绩的方法;
又例如,我们可能需要对其成绩进行排序,存储在一个学生类对象数组之中,因此,要有一个能比较成绩的方法;
下一篇:数据结构之算法的基本概念
http://blog.csdn.net/qq20004604/article/details/50934619