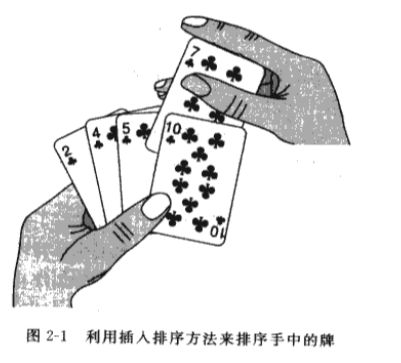
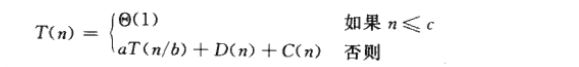插入排序
问题
输入:n个数(a1,a2,···,an).
输出:输入序列的一个排列(即重新排序)(a'1,a'2,···,a'n),使得a'1<=a'2<=···<=a'n。
带排序的数也成为关键字(key)。
排序规则类似打牌
代码实现
+(void)insertionSort:(int *)A length:(int)length{
NSLog(@"插入排序");
NSLog(@"排序前数组:");
printArr(A, length);
for (int j=1; j=0 && A[i]>key) {
A[i+1]=A[i];
i -= 1;
}
A[i+1]=key;
}
NSLog(@"排序后数组:");
printArr(A, length);
}
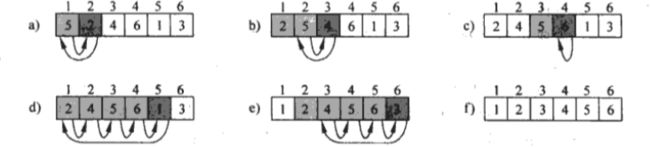
排序规则见图
a.将2 插入到5前面。那么1,2 位置顺序拍好了
b.将4插入到5面前,那么1,2,3位置排序好了
c.将6插入到5后面,那么1,2,3,4位置顺序排好了
d.将1插入到2前面,那么1,2,3,4,5位置顺序排好了
e.将3插入到2后面,那么1,2,3,4,5,6位置就好了
f. 所有顺序就是已排好
插入排序复杂度是n2。
合并排序
分治法 概述
为了解决一个给定的问题,算法要求一次或者多次的递归调用其自身来解决相关的子问题,这种算法通常采用分治策略:将原问题划分成n个规模较小的结构与原问题相似的子问题;递归的解决这些子问题,然后再合并其结果,就得到原问题的解。
分治法的步骤
- 分解:将原问题分解成一系列子问题
- 解决:递归的解决各个子问题,若问题足够小,则直接求解。
- 合并:将子问题的结果合并成原问题的解
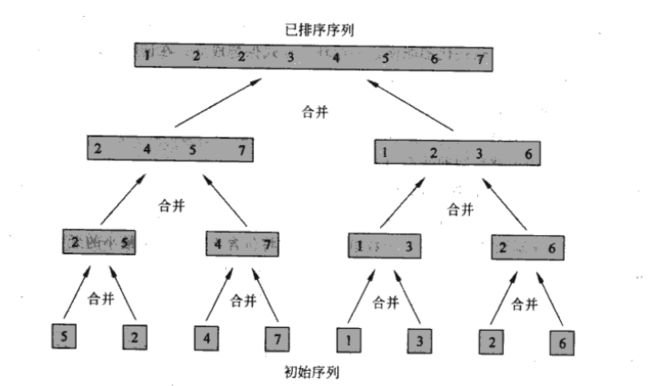
合并排序的合并过程
已扑克牌为例,假设有两堆牌,每一堆都是排序好的,最小的牌在上面。现在我们希望把这两堆牌合并成一幅牌,按照大小顺序排列好。
基本步骤是每次取出两堆牌中最小的一张牌,将其放在输出堆中,重复这个步骤知道结束。
这里我们在每一堆牌中放入结束牌。为了简化代码。
实现代码如下
void merge(int * A ,int begin,int middle,int end){
NSLog(@"merge两个顺序数组");
NSLog(@"排序前数组:");
printArrIndex(A, begin, end);
int n1 = middle-begin+1;
int n2 = end -middle;
int * L=malloc(sizeof(int)*(n1+1));
memset(L, 0, n1+1);
for (int i=0; i合并算法的时间复杂度是n;
合并顺序见图
合并排序实现
void mergeSort(int *A,int begin,int end){
if (begin我们对传入的数组进行排序,要是传入的数组只有一个元素(begin>=end),那么就结束了。
否则,就将数组进行二分拆解。在讲拆解开的数组合并
合并排序的递归公式
时间复杂度是nlgn。
递归排序有数学归纳法的意思
插入排序的递归形式
+(void)insertionRecursionSort:(int *)A length:(int)length{
if (length>1) {
[self insertionRecursionSort:A length:length-1];
}
int last = A[length-1];
int i=length-2;
while (i>=0&&A[i]>last) {
A[i+1]=A[i];
i-=1;
}
A[i+1]=last;
printArr(A, length);
}
二分查找 从排好顺序的数组中查找值v。
算法如下
///数组要求从小到大排列
int binarySearchEqualSortArr(int* A,int begin ,int end,int searchNum){
int result = -1;
int middle = (begin+end)/2;
///说明递归结束了
if (middle==begin) {
if (A[begin]==searchNum) {
result= begin;
}
if (A[end]==searchNum) {
result= end;
}
NSLog(@"二分法数据所在index %d",result);
return result;
}
if (A[middle]==searchNum){
result= middle;
}else if (A[middle]==searchNum){
result= binarySearchEqualSortArr(A, middle, end, searchNum);
}else{
result = binarySearchEqualSortArr(A, begin, middle, searchNum);
}
NSLog(@"二分法数据所在index %d",result);
return result;
}
插入排序的改进
这里只是单纯的用二分法查找策略,改善插入排序。
/*
///时间复杂度
折半插入排序适合记录数较多的场景,与直接插入排序相比,折半插入排序在寻找插入位置上面所花的时间大大减少,但是折半插入排序在记录移动次数方面和直接插入排序是一样的,所以其时间复杂度为O(n2)
。
其次,折半插入排序的记录比较次数与初始序列无关。因为每趟排序折半寻找插入位置时,折半次数是一定的,折半一次就要比较一次,所以比较次数也是一定的。
*/
+(void)insertionSortBinarySearch:(int *)A length:(int)length{
NSLog(@"插入二分法排序");
NSLog(@"排序前数组:");
printArr(A, length);
for (int j=1; jm; k--) {
A[k+1]=A[k];
}
A[m+1]=key;
}
NSLog(@"排序后数组:");
printArr(A, length);
}
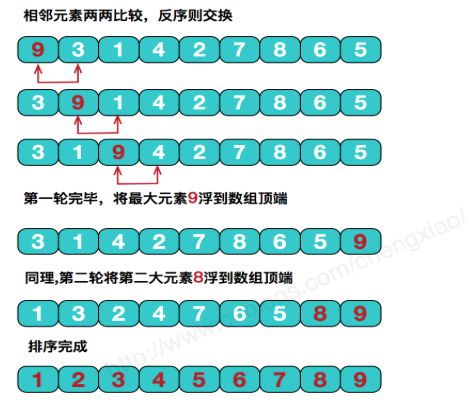
冒牌排序
重复的交换相邻的两个反序元素
///递增排列
void bubbleSort(int *A ,int length){
NSLog(@"冒泡排序");
NSLog(@"排序前数组:");
printArr(A, length);
for (int i=0; ii; j--) {
if (A[j-1]>A[j]) {
exchange(&A[j-1], &A[j]);
}
}
}
NSLog(@"排序后数组:");
printArr(A, length);
}
基础排序总结(冒泡排序、选择排序、插入排序)
冒牌排序效率
比较次数
数组中有 N 个数据项,则第一趟排序中有 N-1 次比较,第二趟中有 N-2 次,以此类推。这种序列的求和公式如下:
(N-1)+(N-2)+(N-3)+…+1=N*(N-1)/2
交换次数
因为两两数据只有在需要时才交换,所以交换的次数少于比较的次数。如果数据是随机的,那么大概有一半数据需要交换,则交换的次数为 N2/4.
选择排序
比较次数
数组中有 N 个数据项,那么第一趟比较1次,第二趟比较2次,最后一趟比较N-1 次,求和公式和冒牌排序一样
(N-1)+(N-2)+(N-3)+…+1=N*(N-1)/2
交换次数
选择排序每次循环只交换一次,因此交换次数是N
插入排序
比较次数
在第一趟排序中最多比较一次,第二趟排序最多比较二次,依次类推,最后一趟,最多比较N-1 次。公式如下
(N-1)+(N-2)+(N-3)+…+1=N(N-1)/2,
因为在插入数据点之前,平均只有全体数据的一半进行了比较。所以这里可以算作比较次数是N(N-1)/4
交换次数
一次交换的次数和比较的次数大致相同是N*(N-1)/4
冒泡排序、选择排序、插入排序比较
冒牌排序:比较次数+交换次数=N2/2 + N2/4 ;
选择排序:比较次数+交换次数=N2/2 + N
插入排序:比较次数+交换次数=N2/4 +N2/4 =N2/2;
因此简单排序中插入排序>选择排序>冒牌排序
算法题 解答
给出一个算法,确定n个元素的任何排列中逆序对的数目
采用的是分治法求解
///求解逆序对
void mergeReverseOrderPair(int * A ,int begin,int middle,int end,int *num){
NSLog(@"merge两个顺序数组");
NSLog(@"排序前数组:");
printArrIndex(A, begin, end);
int n1 = middle-begin+1;
int n2 = end -middle;
int * L=malloc(sizeof(int)*(n1+1));
memset(L, 0, n1+1);
for (int i=0; i源代码地址