高等数学 · 第四章 微分中值定理与导数的应用

第一节 微分中值定理

一、费马定理

定理4.1 （费马定理）

若函数 $f(x)$ 在 $x_0$ 处可导，并且在 $x_0$ 的某邻域内恒有 $f(x)\le f(x_0)$ 或 $f(x)\ge f(x_0)$ 则 $f^{\prime }(x_0)=0$.
证明：不妨设在 $x_0$ 的某邻域内恒有 $f(x)\le f(x_0)$，故 $\forall x_0+\Delta x\in U(x_0),f(x_0+\Delta x)\le f(x_0)$，则 $f^{\prime }(x_0)=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=$$\{\begin{array}{l}{f}_{-}^{\prime }(x_0)\ge 0(\Delta x\to 0^{-})\\ f_{+}^{\prime }(x_0)\le 0(\Delta x\to 0^{+})\end{array}$$\to f^{\prime }(x_0)=0$

费马定理的几何意义

如果 $f(x_0)$ 是函数 $f(x)$ 在 $x_0$ 的某领域内的最大值或最小值，并且曲线 $y=f(x)$ 在点 $(x_0,f(x_0))$ 处有切线，则切线一定是水平的。

补充：极值的定义

如果 $f(x_0)$ 在 $I$ 的某领域内恒有 $f(x)\le f(x_0)$ 或 $f(x)\ge f(x_0)$，则称 $f(x_0)$ 为 $f(x)$ 的一个极大值或极小值，而称 $x_0$ 为极大值点或者极小值点。极大值与极小值统称为 极值，极大值点和极小值点统称为极值点。
如果 $f^{\prime }(x_0)=0$， 则称 $x_0$ 为函数 $f(x)$ 的一个驻点。
因此，费马定理又可表述为：可导的极值点一定是驻点。

二、罗尔定理

定理4.2 罗尔(Rolle)定理

$y=f(x)$ 满足：

1. 在区间 $[a,b]$ 上连续
2. 在区间 $(a,b)$ 内可导
3. $f(a)=f(b)$

$\to$ 在 $(a,b)$ 内至少存在一点使 $f^{\prime }(\xi )=0$
证明：因为 $f(x)$ 在 $[a,b]$ 上连续，故在 $[a,b]$ 上取得最大值 $M$ 和最小值 $m$.
若 $M=m$，则 $f(x)=M,x\in [a,b]$, 因此 $\forall \xi \in (a,b)，f^{\prime }(\xi )=0$.
若 $M>m$, 则 $M$ 和 $m$ 中至少有一个与端点值不等，不妨设 $M\ne f(a)$，则至少存在一个 $\xi \in (a,b)$， 使 $f(\xi )=M$, 则由费马定理得 $f^{\prime }(\xi )=0$.

证明题

已知 $f(x)=x\sqrt{3-x}$，求证： 方程 $f^{\prime }(x)=0$ 在 $(0,3)$ 内至少一根。
解：$\because f(x)$ 在 $[0,3]$ 上连续， 在 $(0,3)$ 内可导，且 $f(0)=f(3)=0$。
$\therefore f(x)$ 在 $[0,3]$ 上满足罗尔定理的条件，故至少有一个点 $\xi \in (0,3)$，使得 $f^{\prime }(\xi )=0$，也就是方程 $f^{\prime }(x)=0$ 在 $(0,3)$ 内至少有一根。

三、拉格朗日中值定理

定理4.3 拉格朗日中值定理

设函数 $y=f(x)$ 满足：

1. 在区间 $[a,b]$ 上连续
2. 在区间 $(a,b)$ 上可导

$\to$ 至少存在一点 $\xi \in (a,b)$，使 $f^{\prime }(\xi )=\frac{f(b)-f(a)}{b-a}$

证明：问题转化为证明 $f^{\prime }(\xi )=\frac{f(b)-f(a)}{b-a}=0$
做辅助函数 $\phi (x)=f(x)-\frac{f(b)-f(a)}{b-a}x$
显然， $\phi (x)$ 在 $[a,b]$ 上连续， 在 $(a,b)$ 内可导，且 $\phi (a)=\frac{bf(a)-af(b)}{b-a}=\phi (b)$，由罗尔定理已知至少存在一点 $\xi \in (a,b)$， 使 $\phi (\xi )=0$

拉格朗日中值定理的几何意义

拉格朗日中值定理说明了怎样的函数具有平行于 A、B 两点连线的切线。

推论1： 若函数 $f(x)$ 在区间 I 上满足 $f^{\prime }(x)=0$，则 $f(x)$ 在 I 上必为常数
推论2： 如果 $f(x)$ 和 $g(x)$ 在 $(a,b)$ 内可导，并且在 $(a,b)$ 内恒有 $f^{\prime }(x)=g^{\prime }(x)$，那么 $f(x)=g(x)+C,\forall x\in (a,b),$ 其中 C 为某个常数。

第二节 洛必达法则

一、洛必达法则定义

定理 4.4 洛必达法则

如果 $f(x)$ 和 $g(x)$ 满足系列条件：

1. $\underset{x\to a}{\lim }f(x)=\underset{x\to a}{\lim }g(x)=0$ 或 $\infty$
2. 在点 $a$ 的某去心领域内，$f(x)$ 与 $g(x)$ 可导，且 $g(x)\ne 0$;
3. $\underset{x\to a}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$存在（或者 $\infty$）

所以$\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$

例题

1. $\underset{x\to 0}{\lim }\frac{e^x-1}{x}.$
   $\underset{x\to 0}{\lim }\frac{e^x-1}{x}=\underset{x\to 0}{\lim }\frac{(e^x-1{)}^{\prime }}{(x{)}^{\prime }}=\underset{x\to 0}{\lim }\frac{e^x}{1}=1$
2. $\underset{x\to \infty }{\lim }\frac{\ln x}{x^a}.$
   $\underset{x\to \infty }{\lim }\frac{\ln x}{x^a}=\underset{x\to \infty }{\lim }\frac{(\ln x{)}^{\prime }}{(x^a{)}^{\prime }}=\underset{x\to \infty }{\lim }\frac{\frac{1}{x}}{a{x}^{a-1}}=\underset{x\to \infty }{\lim }\frac{1}{a{x}^a}=0$
3. $\underset{x\to 0}{\lim }\frac{x-\sin x}{x^3}.$
   $\underset{x\to 0}{\lim }\frac{x-\sin x}{x^3}=\underset{x\to 0}{\lim }\frac{(x-\sin x{)}^{\prime }}{(x^3{)}^{\prime }}=\underset{x\to 0}{\lim }\frac{1-\cos x}{3x^2}=\underset{x\to 0}{\lim }\frac{(1-\cos x{)}^{\prime }}{(3x^2{)}^{\prime }}=\underset{x\to 0}{\lim }\frac{\sin x}{6x}=\frac{1}{6}$

总结，上述 $1$，$3$ 为 $0/0$ 型，$2$ 为 $\infty /\infty$ 型。

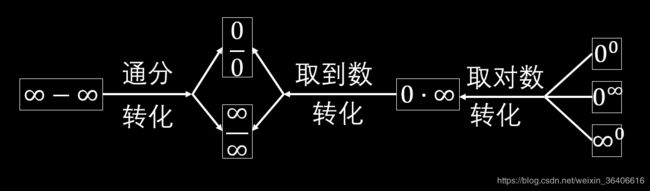
二、 其他类型的未定式子

例题

1. $\underset{x\to 1}{\lim }(\frac{x}{x-1}-\frac{1}{\ln x})$
   $\underset{x\to 1}{\lim }(\frac{x}{x-1}-\frac{1}{\ln x})=\underset{x\to 1}{\lim }(\frac{x\ln x-(x-1)}{\ln x(x-1)})=\underset{x\to 1}{\lim }(\frac{(x\ln x-x+1{)}^{\prime }}{(x\ln x-\ln x{)}^{\prime }})=\underset{x\to 1}{\lim }(\frac{\ln x}{(\ln x+1-\frac{1}{x})})=\underset{x\to 1}{\lim }(\frac{(x\ln x{)}^{\prime }}{(x\ln x+x-1{)}^{\prime }})=\underset{x\to 1}{\lim }(\frac{\ln x+1}{\ln x+2})=\frac{1}{2}$

第三节 函数的单调性

函数的单调性

定理 $4.5$ 设函数 $f(x)$ 在 $[a,b]$ 上连续，在 $(a,b)$ 内可导，

1. 如果在 $(a,b)$ 内 $f^{\prime }(x)>0$，那么函数 $f(x)$ 在 $[a,b]$ 上单调递增。
2. 如果在 $(a,b)$ 内 $f^{\prime }(x)<0$，那么函数 $f(x)$ 在 $[a,b]$ 上单调递减。

证明：$\forall x_1,x_2\in [a,b],$ 设 $x_1<x_2$， 由拉格朗日中值定理： $f(x_2)-f(x_1)=f^{\prime }(\xi )(x_2-x_1)$

例题

1. 讨论函数 $f(x)=3x+x^3$ 的单调性
   解：函数在定义域内连续并且 $f^{\prime }(x)=3-3\ast x^2=3(1-x)(1+x)$
   

第四节 函数的极值及其求法

函数的极值

定理4.6 （必要条件） 如果 $x_0$ 是函数 $f(x)$ 的极值点， 则 $x_0$ 必为函数 $f(x)$ 的驻点 或 不可导点，亦即， $f^{\prime }(x_0)=0$ 或 $f^{\prime }(x_0)$ 不存在。

函数极值的求法

定理 4.7 (第一充分条件)

设函数$f(x)$ 在点 $x_0$ 的某领域 $(x_0-\delta ,x_0+\delta )$ 内连续，在去心领域内可导

1. 如果 $x\in (x_0-\delta ,x_0)$ 时， $f^{\prime }(x)>0$； 当 $x\in (x_0,x_0+\delta )$ 时，$f^{\prime }(x)<0$，那么函数 $f(x)$ 在 $x_0$ 处取得极大值。
2. 如果 $x\in (x_0-\delta ,x_0)$ 时， $f^{\prime }(x)<0$； 当 $x\in (x_0,x_0+\delta )$ 时，$f^{\prime }(x)>0$，那么函数 $f(x)$ 在 $x_0$ 处取得极小值。
3. 如果当 $x\in (x_0-\delta ,x_0)\bigcup (x_0,x_0+\delta )$ 时，恒有 $f^{\prime }(x)>0$，或恒有 $f^{\prime }(x)<0$； 那么函数 $f(x)$ 在 $x_0$ 处没有极值。

定理4.8 （第二充分条件）

设函数$f(x)$ 在点 $x_0$ 的某领域 $(x_0-\delta ,x_0+\delta )$ 内连续，存在二阶导数，并且 $f^{\prime }(x_0)=0,f^{\prime \prime }(x_0)\ne 0$

1. 若 $f^{\prime \prime }(x)<0$，则函数 $y=f(x)$ 在 $x_0$ 处取得极大值；
2. 若 $f^{\prime \prime }(x)<0$，则函数 $y=f(x)$ 在 $x_0$ 处取得极小值。

例题

1. 计算 $y=-x^4+2x^2$ 的极值
   解：$y^{\prime }=-4x^3+4x=-4x(x-1)(x+1)$
   令 $y^{\prime }=0$ 时，则驻点为： $x_1=-1,x_2=0,x_3=1$
   又 $y^{\prime \prime }=-12x^2+4$
   $y^{\prime \prime }(-1)=y^{\prime \prime }(1)=-8<0,y^{\prime \prime }(0)=4>0$
   由定理 $4.8$ 判断，$x_1=-1,x_3=1$ 处取得极大值 $1$，$x_2=1$处取得极小值 $0$.

第五节 函数的最大值和最小值及其应用

函数的最值

假定函数 $f(x)$ 在闭区间 $[a,b]$ 上连续，在开区间 $(a,b)$ 内最多有有限个驻点和导数不存在的点。则由上面的分析知，函数$f(x)$在 $[a,b]$上的最大值和最小值要么在端点 $a,b$ 处达到，要么是极值，从而在某个极值点处达到。 而由极值的必要条件知， 极值点要么是驻点，要么是函数的不可导点。因此，函数 $f(x)$ 在 $[a,b]$ 上的最大值和最小值只可能在端点 $a,b,f(x)$ 的驻点，或者不可导点处取到，故只需要求出这些点处的函数值并加以比较：其中最大的即为最大值，最小的即为最小值。

具体归纳出来可以按一下步骤求满足上述条件的函数的极值：

1. 求出 $f(x)$ 在 $(a,b)$ 上的所有驻点和导数不存在的点；
2. 求出驻点，导数不存在的点以及端点的函数值；
3. 比较函数在端点、驻点、不可导点处的值，最大的即为最大值，最小的即为最小值。

第六节 函数的凹凸性和拐点

凹凸性的定义

设函数 $y=f(x)$ 在区间 $I$ 上连续。如果对任意的 $x_1,x_2\in I$ 且 $x_1\ne x_2$ 恒有 $f(\frac{x_1+x_2}{2})<\frac{f(x_1)+f(x_2)}{2}$，则称函数 $f(x)$ 的曲线在区间 $I$ 上是凹 的；如果恒有 $f(\frac{x_1+x_2}{2})>\frac{f(x_1)+f(x_2)}{2}$ 则称函数 $f(x)$ 的曲线在区间 $I$ 上是凸的；

函数的凹凸性

设函数 $f(x)$ 在闭区间 $[a,b]$ 上连续，在 $(a,b)$ 内具有二阶导数。

1. 若在 $(a,b)$ 内 $f^{\prime \prime }(x)>0$，则函数 $f(x)$ 在 $[a,b]$ 上的曲线是凹的；
2. 若在 $(a,b)$ 内 $f^{\prime \prime }(x)<0$，则函数 $f(x)$ 在 $[a,b]$ 上的曲线是凸的；

拐点

连续函数 $f(x)$ 的图像上的凹凸性的分界点称为函数的拐点
按以下步骤求函数的拐点以及凹凸区间：

1. 求 $f^{\prime \prime }(x)$ ，并求出在所讨论区间内的 $f^{\prime \prime }(x)$ 不存在的点；
2. 求 $f^{\prime \prime }(x)=0$， 求出位于所讨论区间的所有实根；
3. 讨论 $f^{\prime \prime }(x)$ 在以上求出的区间内 $f^{\prime \prime }(x)=0$ 的点以及 $f^{\prime \prime }(x)$ 不存在的点的左右两侧的符号，确定该点是否为拐点。