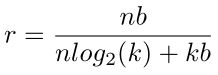韩松Deep compression论文讲解——PPT加说明文字
本文为Deep compression的论文笔记,相应的ppt及文字讲解
原论文《 Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman coding》https://arxiv.org/abs/1510.00149
相关论文
深鉴科技FPGA2017最佳论文ESE Efficient speech recognition engine with sparse LSTM on FPGA论文详解
PipeCNN论文详解:用OpenCL实现FPGA上的大型卷积网络加速
韩松EIE:Efficient Inference Engine on Compressed Deep Neural Network论文详解
韩松博士毕业论文Efficient methods and hardware for deep learning论文详解
目录
一、摘要
意义
方法
作用
二、方法
2.1 剪枝
稀疏矩阵的存储
2.2 权值量化与共享
聚类方法
权值更新方法Fine-tune
意义
压缩率
量化没有降低数据精度
2.3 初始化权重的值
2.4 哈夫曼编码
可压缩性
哈夫曼编码
三、实验
四、结论
Deep compression是一篇关于模型压缩的论文,这篇文章是ICLR2016年的best paper。作者韩松是专门做模型压缩和机器学习硬件加速的。这篇文章通过剪枝,权值共享和权值量化的方法把一些经典的深度学习模型压缩了非常多倍,取得了很好的效果。
一、摘要
意义
模型压缩一直是机器学习的一个重要方向,并且一个模型不可能只在GPU和服务器上运行才可以。只有通过硬件化实现才能落地。但是神经网络也是非常耗费存储和耗费运算的。本文希望通过一些方法把原本耗费大量存储和运算的神经网络实现在硬件上。
方法
本文采用的方法是剪枝,权值共享和权值量化,还有哈夫曼编码的方法。
- 剪枝就是去掉一些不必要的网络权值,只保留对网络重要的权值参数;
- 权值共享就是多个神经元见的连接采用同一个权值,权值量化就是用更少的比特数来表示一个权值。
- 对权值进行哈夫曼编码能进一步的减少冗余。
作用
作者在经典的机器学习算法,AlexNet和VGG-16上运用上面这些模型压缩的方法,在没有精度损失的情况下,把AlexNet模型参数压缩了35倍,把VGG模型参数压缩了49倍,并且在网络速度和网络能耗方面也取得了很好的提升。
二、方法
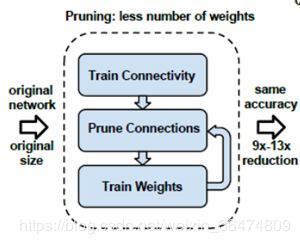
首先,网络通过正常的训练,训练出相应的权重,然后把低于某个阈值的权重删除掉,然后再训练模型,一次次去掉冗余的链接。
然后网络把保留的权重进行聚类和权值共享,然后通过训练不断调整聚类的中心点和聚类的数量,然后将最后的权值和权值索引进行哈夫曼编码。达到模型压缩的效果。下面详细讲解这些步骤。
2.1 剪枝
剪枝生成的稀疏矩阵:首先是剪枝,首先通过正常训练相应的网络,然后设置一个阈值,把小于阈值的连接置为0,然后重新对网络进行训练,重复上面两个步骤来减少相应的权重连接。然后我们得到的是一个稀疏的权值矩阵。
1. Learning the connectivity via normal network training.
通过正常方法训练网络
2. We prune the small-weight connections: all connections with weights below a threshold are removed from the network.
将小于某个阈值的权重扔掉,设为0不再训练
3. We retrain the network to learn the final weights for the remaining sparse connections.
重新训练相应的网络剩下的权重
稀疏矩阵的存储
稀疏权值矩阵的存储:比如我们这个稀疏的矩阵里面,n×n的矩阵,里面大多数的值是零值,然后我们通过相应的存储稀疏矩阵的方式对这个矩阵进行存储。首先把所有的非零值存为AA,假设所有的非零值的元素的个数为a,然后把每一行第一个非零元素对应在AA的位置存为JA,最后一个数是所有非零元素的个数+1,所以JA中的元素就是行数n+1,然后把AA中每一个元素在原始矩阵中的列存为IC。所以我们把一个原始的n×n的稀疏矩阵存为2a+n+1个数字。
![]()
剪枝之前的矩阵是非稀疏的矩阵,例如一个n*n的矩阵,经过剪枝的过程之后,这个n*n的矩阵就变为一个n*n的稀疏矩阵,其中很多零值。可以采用CSR或者CSC的方法对这个矩阵进行存储从而减少相应的存储量。
例如CSC的存储稀疏矩阵的方法
第一行AA存储所有的非零元素,
第二行JA存储所有系数矩阵中每行第一个非零元素在AA的位置,例如第一个元素是4.0,在AA中位置是第一个,第二行第一个元素是4.0,在AA中位置是第四个。通过JA可以将AA中所有元素对应的行恢复出来。
第三行JC是所有元素对应的列标。
这样,一个稀疏的矩阵通过三行就能存下来,达到了很好的存储压缩。由N*N变为了2a+N+1个元素
相对位置的参数:在压缩完参数之后,我们存了权值和权值对应的参数。之前的参数存的是绝对的参数,我们现在存相对的参数,就是两个参数的差值,比如我们用三个特存相对的参数,只要两个元素的距离小于8,都能把参数存为3个比特的,如果两个参数的距离大于这个值,我们就在第8个位置设置一个0值。
![]()
通过CSC得到了压缩的矩阵,可以通过差分存储进一步压缩存储数量。例如我们想用三比特的值来存储相应的Index。
3bit可以容忍的间距为8
- 当间距小于8时:用3比特的值就可以恢复出相应的位置
- 当间距大于8时:在第8个位置插入0值,然后用3bit的与插入的0值的差分位置恢复出相应的位置
- 间距大于8的倍数时:每隔8个位置插入0值,与最后一个0值的3bit的差分位置恢复出位置
2.2 权值量化与共享
在进行了剪枝之后,我们只保留了重要的权值,然后我们对这些权值进行k-means的聚类。
比如我们聚类数量是k,那么表示该类需要用的的比特数是log2(k),然后我们采用聚类中心点的值作为类内共享的权值。比如图中,相同颜色的权值就在同一类之中,他们共享聚类中心点的权值。这样,我们只需要存储每一个权值属于哪一类,需要log2(k)个比特,和每一类的中心点的值。
聚类方法
运用K-means的聚类方法,将权值接近的共享。运用聚类中心点的值作为所有权值的值。例如上面相同颜色的就是同一个聚类的。
权值更新方法Fine-tune
将所有聚类的点的梯度相加作为权值中心的梯度用于更新权值。
意义
1.Reducing the number of bits required to represent each weight.
减少每一个权重的表示需要的比特数
2.Limit the number of effective weights we need to store by having multiple connections share the same weight.
减少需要存储的权重个数(权值共享)
3.Fine-tune those shared weights.
可以共同对共享的权值进行微调与训练
压缩率
- 压缩前分子:原始权值的个数n,原始权重的比特数b,相乘得到原始总权值需要的比特数
- 压缩后分母:n为权重的个数,log2(k)表示聚类后的每一类的比特数。用这个可以恢复出共享的每一个权值属于哪一类,k为聚类书,b为之前的需要存储的精度,用这个可以恢复出每一个聚类的中心点的位置。
压缩率可以这样得出来,分子n是有n个权值要存储,b就是原始的每个权值的比特数,nb就是原来需要存储这些权值需要的比特数。分母n乘以log2(k)就是这n个权值需要乘以log2(k)个比特来表示每个权值的类,然后kb是所有类的中心点需要耗费的存储。
相应的梯度是这样更新的,只需要更新聚类的中心点的位置就好,我们把聚类内对应位置的梯度加起来,作为新的梯度,乘上学习率然后用聚类内中心点减去这个值。
量化没有降低数据精度
需要关注的一个问题是,量化没有降低数据的精度,也没有缩减运算。因为存储的减少是权值共享带来的,可以用更少的比特数来代表相应的权值。但是共享后的权值精度还是与之前一样。
2.3 初始化权重的值
权值共享的是聚类中心点的位置,初始的聚类中心点是如何确定的呢?有三种方法可以确定聚类中心点的位置。一是随机的方法,就是在权值中随机的选k个值做为聚类中心点。还有一种是基于密度的初始化,我们可以看这个图,横轴是对应的权值的值,纵轴是权值的数量,类似于直方图一样。红色的线是权值的直方图统计,蓝色的线是权值的累积统计,类似于概率密度函数和概率累积函数。基于密度的初始化就是把权值从小到大等分成k份,然后每一份分界点的权值就是聚类的中心。线性的初始化就是直接把最小值最大值之间直接线性进行划分。
因为网络中大的权值往往是更重要的,前两种方法容易让聚类的中心点往概率密度大的地方累积,而线性分类法权值更容易是大的。所以线性的初始化方法比较好,通过后面的实验,也发现通过线性的分类方法取得了更好的准确率。
2.4 哈夫曼编码
哈夫曼编码运用字符出现的概率来进行编码,只要不是均匀分布的,哈夫曼编码就能减少一定的冗余,比如在AlexNet中,相应的权值的直方图和权值参数的直方图是上面这两种,用哈夫曼编码可以减少20-30%的信息冗余。
可压缩性
但是这个表具有进一步压缩的潜能,因为其分布不是均匀分布。上面直方图体现了权值与location Idx的分布不是均匀分布。
哈夫曼编码
所以采用哈夫曼编码的方法,用短码代表出现频率高的权重,用长码替代出现频率低的权重,进一步对网络进行压缩。
三、实验
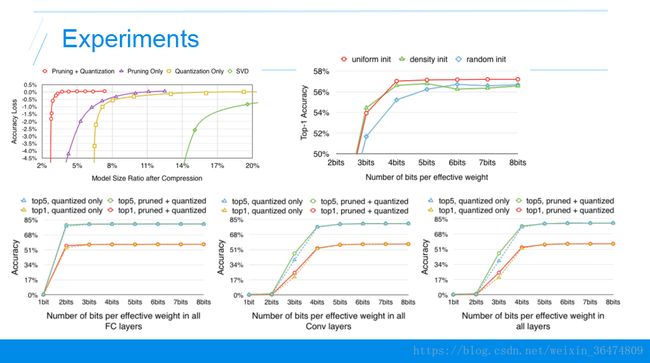
首先第一个实验,不同压缩方法在不同压缩率下精度的损失。横轴是压缩率,越靠左压缩率越大,纵轴是精度的损失,就是压缩之前和压缩之后的准确率的减少的量。这条曲线越靠左上越好,表明更大压缩率下精度损失更少,我们看到最好的方法就是剪枝和权值共享和权值量化的方法。
然后就是权值共享过程中,聚类的初始化值对实验结果的影响,三条曲线分别是上面讲到的三种不同的聚类方法。横轴是压缩的比特数,越靠左表明压缩的比率越大,纵轴是准确率,表明随着压缩的越来越少的比特数,精度越来越低,所以曲线越靠上越好。效果最好的是红色的这条线,就是我们初始聚类初始化的时候,采用线性初始化的方法能达到最好的效果。
下面这三个图表示不同的压缩率对不同层的影响,第一个是压缩的比特数对全连接层的影响,第二个是压缩的比特数对卷积层的影响,第三个是两个层的压缩比特数对实验结果的影响,我们发现卷积层比全连接层对压缩的比特数更加敏感。
然后就是相应的实验,AlexNet压缩了35倍,把VGG压缩了49倍,相比其他的压缩方法,作者的方法没有精度损失并且达到了最大的压缩率。
四、结论