高性能MySql--01（数据库索引）

1.什么是索引？

   索引是对数据库表中一列或多列值进行排序的一种结构，使用索引可以提高数据库中特定数据的查询速度，索引是一个单独的，存储在磁盘上的数据结构，它包含着对数据表里所有记录的引用指针。

索引是在存储引擎中实现的，每种存储引擎的索引也不一定完全相同。

MySql中索引的存储类型有两种：Btree和Hash

 索引的优缺点：

               

   索引的分类：

          

   索引的设计原则：

           

 

以下内容均为从大神的博客上直接摘抄整理 参考链接全部给出~~~~~~

2.理解索引：抛出问题

     为什么要给表加上主键？

     为什么加索引后会使查询变快？

     为什么加索引后会使写入、修改、删除变慢？

     什么情况下要同时在两个字段上建索引？

想要理解索引原理必须清楚一种数据结构「平衡树」(非二叉)，也就是b tree或者 b+ tree，重要的事情说三遍：“平衡树，平衡树，平衡树”。当然， 有的数据库也使用哈希桶作用索引的数据结构 ， 然而， 主流的RDBMS都是把平衡树当做数据表默认的索引数据结构的。

我们平时建表的时候都会为表加上主键， 在某些关系数据库中， 如果建表时不指定主键，数据库会拒绝建表的语句执行。 事实上， 一个加了主键的表，并不能被称之为「表」。一个没加主键的表，它的数据无序的放置在磁盘存储器上，一行一行的排列的很整齐， 跟我认知中的「表」很接近。如果给表上了主键，那么表在磁盘上的存储结构就由整齐排列的结构转变成了树状结构，也就是上面说的「平衡树」结构，换句话说，就是整个表就变成了一个索引。没错， 再说一遍， 整个表变成了一个索引，也就是所谓的「聚集索引」。 这就是为什么一个表只能有一个主键， 一个表只能有一个「聚集索引」，因为主键的作用就是把「表」的数据格式转换成「索引（平衡树）」的格式放置。

                              

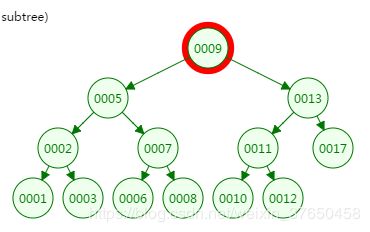
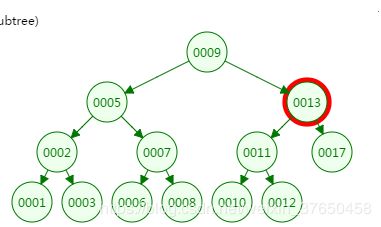
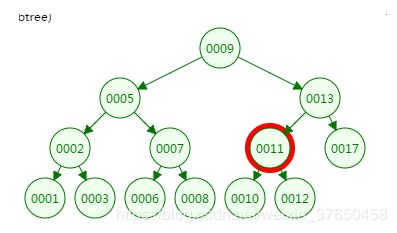
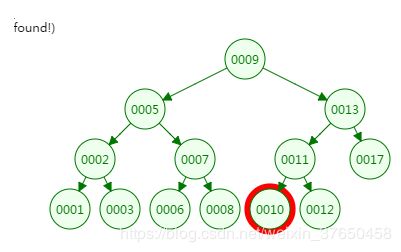
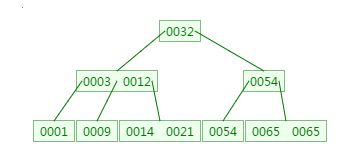
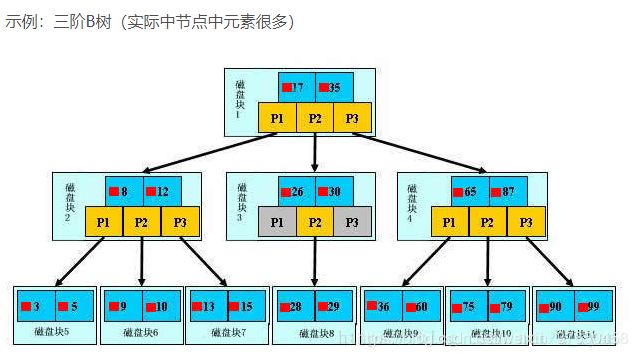
假如我们执行一个SQL语句：select * from table where id = 1256;

首先根据索引定位到1256这个值所在的叶结点，然后再通过叶结点取到id等于1256的数据行。 这里不讲解平衡树的运行细节， 但是从上图能看出，树一共有三层， 从根节点至叶节点只需要经过三次查找就能得到结果。如下图

                           

 索引能让数据库查询数据的速度上升， 而使写入数据的速度下降，原因很简单的， 因为平衡树这个结构必须一直维持在一个正确的状态， 增删改数据都会改变平衡树各节点中的索引数据内容，破坏树结构， 因此，在每次数据改变时， DBMS必须去重新梳理树（索引）的结构以确保它的正确，这会带来不小的性能开销，也就是为什么索引会给查询以外的操作带来副作用的原因。

非聚集索引， 也就是我们平时经常提起和使用的常规索引。

非聚集索引和聚集索引一样， 同样是采用平衡树作为索引的数据结构。索引树结构中各节点的值来自于表中的索引字段， 假如给user表的name字段加上索引 ， 那么索引就是由name字段中的值构成，在数据改变时， DBMS需要一直维护索引结构的正确性。如果给表中多个字段加上索引 ， 那么就会出现多个独立的索引结构，每个索引（非聚集索引）互相之间不存在关联。 如下图

                       

每次给字段建一个新索引， 字段中的数据就会被复制一份出来， 用于生成索引。 因此， 给表添加索引，会增加表的体积， 占用磁盘存储空间。

非聚集索引和聚集索引的区别在于， 通过聚集索引可以查到需要查找的数据， 而通过非聚集索引可以查到记录对应的主键值 ， 再使用主键的值通过聚集索引查找到需要的数据，如下图

                       

  不管以任何方式查询表， 最终都会利用主键通过聚集索引来定位到数据， 聚集索引（主键）是通往真实数据所在的唯一路径。

  有一种例外可以不使用聚集索引就能查询出所需要的数据， 这种非主流的方法 称之为「覆盖索引」查询， 也就是平时所说的复合索引或者多字段索引查询

  

先看下面这个SQL语句

//建立索引

create index index_birthday on user_info(birthday);

//查询生日在1991年11月1日出生用户的用户名

select user_name from user_info where birthday = '1991-11-1'

这句SQL语句的执行过程如下

首先，通过非聚集索引index_birthday查找birthday等于1991-11-1的所有记录的主键ID值

然后，通过得到的主键ID值执行聚集索引查找，找到主键ID值对就的真实数据（数据行）存储的位置

最后， 从得到的真实数据中取得user_name字段的值返回， 也就是取得最终的结果

我们把birthday字段上的索引改成双字段的覆盖索引

create index index_birthday_and_user_name on user_info(birthday, user_name);

这句SQL语句的执行过程就会变为

通过非聚集索引index_birthday_and_user_name查找birthday等于1991-11-1的叶节点的内容，然而， 叶节点中除了有user_name表主键ID的值以外， user_name字段的值也在里面， 因此不需要通过主键ID值的查找数据行的真实所在， 直接取得叶节点中user_name的值返回即可。 通过这种覆盖索引直接查找的方式， 可以省略不使用覆盖索引查找的后面两个步骤， 大大的提高了查询性能，如下图

                 

 3.  磁盘IO与预读    

       数据库的数据存放在磁盘上面，这也是数据库数据能持久化的原因，但是磁盘读取依靠的是机械运动，分为寻道时间、旋转延迟、传输时间三个部分，这三个部分耗时相加就是一次磁盘IO的时间，大概9ms左右。这个成本是访问内存的十万倍左右；正是由于磁盘IO是非常昂贵的操作，所以计算机操作系统对此做了优化：预读；每一次IO时，不仅仅把当前磁盘地址的数据加载到内存，同时也把相邻数据也加载到内存缓冲区中。因为局部预读原理说明：当访问一个地址数据的时候，与其相邻的数据很快也会被访问到。每次磁盘IO读取的数据我们称之为一页（page）。一页的大小与操作系统有关，一般为4k或者8k。这也就意味着读取一页内数据的时候，实际上发生了一次磁盘IO。

      正因为有了磁盘IO预读机制，所以才有了减少磁盘IO的可能，因为一次磁盘IO操作，可以查找到物理存储中相邻的一大片数据。一次磁盘IO操作可以取出物理存储中相邻的一大片数据，如果查询的索引数据（就是B+树中从根节点一直到叶子节点整个过程中查询的节点数）都集中在该区域，那么只需要一次磁盘IO，否则就需要多次磁盘IO

正是基于磁盘IO预读机制的前提，数据库可以采用索引机制快速查询出数据。

举个例子来说，假设我们有一个数据库student，这个表分别有三个字段：name，age，class。假设表中有2000条记录。

       1、假如没有使用索引，当我们查询名为“xiaxia”的学生的时候，即调用：

            select name,age,class from student where name = "xiaxia";
      此时数据库不得不在student表中对这2000条记录一条一条的进行判断name字段是否为“xiaxia”。这也就是所谓的全表扫描。

     2、而当我们在student表上的name字段上创建索引时，当我们查询名为“xiaxia”的学生时：

         会通过索引查找去查询名为“xiaxia”的学生，因为该索引已经按照字母顺序排列，因此要查找名为“xiaxia”的记录时会快很多，因为名字首字母为“x”的雇员都是排列在一起的。通过该索引，能获取到表中对应的记录。

 所以B树的出现不是为了减小查询的时间复杂度，而是减小磁盘IO操作，众所周知，ＩＯ操作的效率很低，那么，当在大量数据存储中，查询时我们不能一下子将所有数据加载到内存中，只能逐一加载磁盘页，每个磁盘页对应树的节点。造成大量磁盘ＩＯ操作（最坏情况下为树的高度）。平衡二叉树由于树深度过大而造成磁盘IO读写过于频繁，进而导致效率低下。 
　　所以，我们为了减少磁盘ＩＯ的次数，就你必须降低树的深度，将“瘦高”的树变得“矮胖”。一个基本的想法就是： 
　　（1）、每个节点存储多个元素 
　　（2）、摒弃二叉树结构，采用多叉树

这样就引出来了一个新的查找树结构 ——多路查找树。 根据AVL给我们的启发，一颗平衡多路查找树(B~树)自然可以使得数据的查找效率保证在O(logN)这样的对数级别上。

   二叉树查询过程：

      我们先来看二叉树查找时磁盘IO的次：定义一个树高为4的二叉树，查找值为10：

                                   

     第一次磁盘IO：

                                       

   第二次磁盘IO：

                                          

   第三次磁盘IO:

                                        

第四次磁盘IO：

                                        

 从二叉树的查找过程了来看，树的高度和磁盘IO的次数都是4，所以最坏的情况下磁盘IO的次数由树的高度来决定。

从前面分析情况来看，减少磁盘IO的次数就必须要压缩树的高度，让瘦高的树尽量变成矮胖的树，所以B-Tree就在这样伟大的时代背景下诞生了。

B-Tree查询过程：

      如下有一个3阶的B树，观察查找元素21的过程：

                                                 

    第一次磁盘IO：  

                                               

   第二次磁盘IO：

                                               

  

这里有一次内存比对：分别跟3与12比对                           

第三次磁盘IO:

                                          

这里有一次内存比对，分别跟14与21比对

从查找过程中发现，B树的比对次数和磁盘IO的次数与二叉树相差不了多少，所以这样看来并没有什么优势。

但是仔细一看会发现，比对是在内存中完成中，不涉及到磁盘IO，耗时可以忽略不计。另外B树种一个节点中可以存放很多的key（个数由树阶决定）。

相同数量的key在B树中生成的节点要远远少于二叉树中的节点，相差的节点数量就等同于磁盘IO的次数。这样到达一定数量后，性能的差异就显现出来了。

 

下面来具体介绍一下B树（Balance Tree），

4.理解Ｂ树：

一个m阶的B树具有如下几个特征：B树中所有结点的孩子结点最大值称为B树的阶，通常用m表示。一个结点有k个孩子时，必有k-1个关键字才能将子树中所有关键字划分为k个子集。

1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子，其中 ceil（m/2） ≤ k ≤ m
3.每一个叶子节点都包含k-1个元素，其中 ceil（m/2） ≤ k ≤ m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
6.每个结点的结构为：（n，A0，K1，A1，K2，A2，…  ，Kn，An）
    其中，Ki(1≤i≤n)为关键字，且Ki Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。
n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。
 

查询
　　以上图为例：若查询的数值为５： 
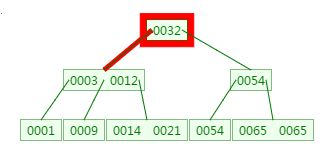
　　第一次磁盘ＩＯ：在内存中定位（与17、35比较），比17小，左子树； 
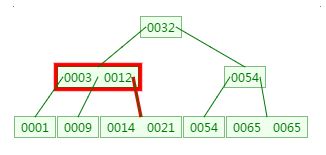
　　第二次磁盘ＩＯ：在内存中定位（与８、12比较），比８小，左子树； 
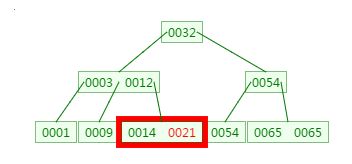
　　第三次磁盘ＩＯ：在内存中定位（与3、5比较），找到5，终止。 
整个过程中，我们可以看出：比较的次数并不比二叉查找树少，尤其适当某一节点中的数据很多时，但是磁盘IO的次数却是大大减少。比较是在内存中进行的，相比于磁盘IO的速度，比较的耗时几乎可以忽略。所以当树的高度足够低的话，就可以极大的提高效率。相比之下，节点中的元素多点也没关系，仅仅是多了几次内存交互而已，只要不超过磁盘页的大小即可。

插入：

                           

   

第一步：检索key插入的节点位置如上图所示，在3,5之间；

第二步：判断节点中的关键码个数： 
　　节点3，5已经是两元素节点，无法再增加。父亲节点 2， 6 也是两元素节点，也无法再增加。根节点9是单元素节点，可以升级为两元素节点。；

第三步：结点分裂： 
　　拆分节点3，5与节点2，6，让根节点9升级为两元素节点4，9。节点6独立为根节点的第二个孩子。

最终结果如下图：虽然插入比较麻烦，但是这也能确保Ｂ树是一个自平衡的树                     
                         

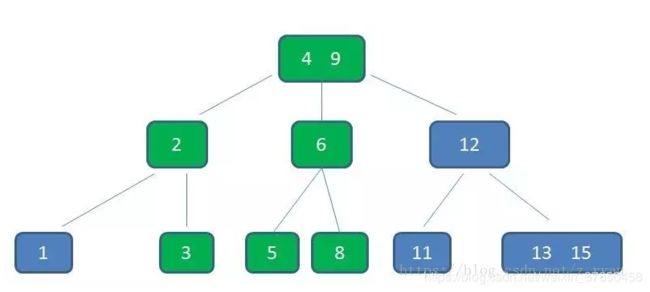
删除和增加修改都会改变树的结构，使树重新平衡，这个代价极大。

  B+ 树：Ｂ＋树是Ｂ树的变种，有着比Ｂ树更高的查询效率。

1.有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据
都保存在叶子节点。

2.所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小
自小而大顺序链接。

3.所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

                        

 

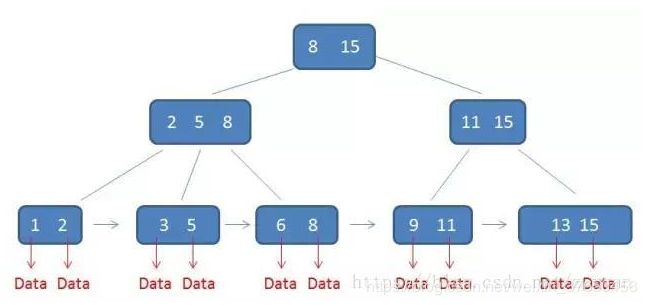
B+树的优势在于查找效率上，下面我们做一具体说明： 
　　首先，Ｂ＋树的查找和Ｂ树一样，类似于二叉查找树。起始于根节点，自顶向下遍历树，选择其分离值在要查找值的任意一边的子指针。在节点内部典型的使用是二分查找来确定这个位置。 
　　（1）、不同的是，Ｂ＋树中间节点没有卫星数据（索引元素所指向的数据记录），只有索引，而Ｂ树每个结点中的每个关键字都有卫星数据；这就意味着同样的大小的磁盘页可以容纳更多节点元素，在相同的数据量下，Ｂ＋树更加“矮胖”，ＩＯ操作更少 
　　B树的卫星数据： 
                   

     B+树的卫星数据：

                        

需要补充的是，在数据库的聚集索引（Clustered Index）中，叶子节点直接包含卫星数据。在非聚集索引（NonClustered Index）中，叶子节点带有指向卫星数据的指针。 
　　 
　　（2）、其次，因为卫星数据的不同，导致查询过程也不同；Ｂ树的查找只需找到匹配元素即可，最好情况下查找到根节点，最坏情况下查找到叶子结点，所说性能很不稳定，而Ｂ＋树每次必须查找到叶子结点，性能稳定 
　　（3）、在范围查询方面，B+树的优势更加明显 
　　B树的范围查找需要不断依赖中序遍历。首先二分查找到范围下限，在不断通过中序遍历，知道查找到范围的上限即可。整个过程比较耗时。 
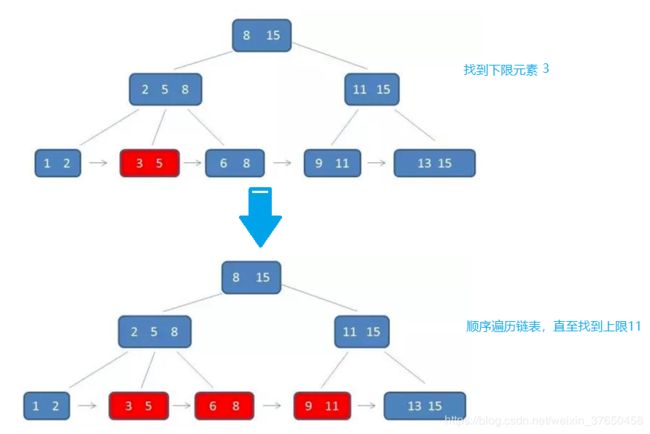
　　而B+树的范围查找则简单了许多。首先通过二分查找，找到范围下限，然后同过叶子结点的链表顺序遍历，直至找到上限即可，整个过程简单许多，效率也比较高。 
　　例如：同样查找范围[3-11]，两者的查询过程如下： 
　　B树的查找过程： 

B+树的查找过程：

   B+树相比B树的优势： 
　　1.单一节点存储更多的元素，使得查询的IO次数更少； 
　　2.所有查询都要查找到叶子节点，查询性能稳定； 
　　3.所有叶子节点形成有序链表，便于范围查询。

5.面试：

   MySQL数据库中的索引为什么能够加快查询速度？

      MySQL中的索引是B+树，使用B+树查找数据的时间复杂度度为O(logN).索引中的叶子节点是连在一起的，这会加快范围查询。 如下图所示（InnoDB），查找订单号在18到49的全部订单。首先通过从根节点开始查找，找到订单号为18的叶子节点，然后从当前的叶子节点向后查找，直到找到订单号为49的订单才停止查找。遍历的叶子节点皆作为查询结果返回。

  倘若将索引改成B树，BST，AVL， 或红黑树，可以吗？

B+树 vs. B树 
- 减少磁盘访问次数 
B树的非叶子节点包含了关键字和指向关键字具体信息的指针，而叶子节点不含任何关键信息；而B+树非叶子节点不含指向关键字的指针，只是叶子节点关键字的索引，叶子节点才包含指向关键字信息。因此，B+树内部节点比B树小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。 
- 查询效率更加稳定 
B树搜索可能在非叶子节点结束，也靠近根节点的记录查找时间越短，而查询不存在的关键字，仍需要从根节点走到叶子节点才能确定。而在B+树中，任何关键字的查找都必须走一条从根节点到叶节点的路径，查找路径相同，导致每个关键字查询效率相当。尽管B+树找到一个记录所需的比较次数要比B-树多，但是一次磁盘访问的时间相当于成百上千次内存比较的时间，因此实际中B+树的性能可能还会好些。 
- B树不支持顺序遍历 
B+树的叶子节点使用指针顺序连接在一起，只要遍历叶子节点就可以实现整棵树的遍历。而数据库中的范围查询是非常频繁的，而B树顺序遍历效率比较低。
二分查找（BST）树 
BST树的深度不可控，最糟糕的情况是BST变成单向链表，深度较大的BST不但会增加磁盘IO，也会影响查找效率。
平衡二叉树（AVL） 
与BST相比，虽然能够保证绝对平衡，保证了查找效率，但是维护AVL树平衡的开销比较大，尤其对于插入删除频繁的业务场景而言，绝对平衡带来的查找效率优势就不再那么明显了。
红黑树 
红黑树虽然解决了AVL树维护平衡开销比较大的问题，但是红黑树跟B树一样，非叶子节点也会存储数据，同样面临跟B树同样的问题，磁盘IO负担大。此外，红黑树分支因子比较少，深度比B+树更深，那么在查找时页缺失的概率也随之增大。

  哈希(hash)比树(tree)更快，索引结构为什么要设计成树型？
  索引设计成树形，和SQL的需求相关。 
对于这样一个单行查询的SQL需求：select * from t where name=”shenjian”; 
确实是哈希索引更快，因为每次都只查询一条记录。所以，如果业务需求都是单行访问，例如passport，确实可以使用哈希索引。 
但是对于排序查询的SQL需求：分组：group by; 排序：order by; 比较：<、> 
哈希型的索引，时间复杂度会退化为O(n)，而树型的“有序”特性，依然能够保持O(log(n)) 的高效率。
 

 

参考博客：https://www.cnblogs.com/aspwebchh/p/6652855.html 深入理解数据库索引

                  https://blog.csdn.net/qq_35571554/article/details/82796278  理解磁盘io与预读

                  https://blog.csdn.net/programmer_at/article/details/82735128 为什么数据库索引要用b树

                  https://blog.csdn.net/z_ryan/article/details/79685072  理解B树