机器学习中L1L2规则化详解（先验及稀疏性解释）
（作者：陈玓玏）
1、 为什么要正则化?
知乎上有个兄弟说得对（https://www.zhihu.com/question/20924039 这个问题下Stark Einstein的回答），不应该说是正则化，应该说是规则化，也就是说，我们原来是在完全没有任何先验知识的情况下进行的训练，那训练出来的结果有可能会“过”，你不知道哪个特征会有用，于是你找了很多特征，尽可能精确地去拟合你的训练数据，结果用上了一些其实不重要的特征，这些特征在训练集中表现不错，但是在测试集中却不重要，也就是说这些特征本身就不具备普适性，但你还学习到它了，在这种不具备普遍性的情况下学习到它，自然会影响你测试集的效果，自然就做不出泛化能力强的模型，就产生了过拟合。当然了，并不是只要参数一多就会过拟合，还要看你的样本量。
规则化的另外一个意义是减少不必要的特征，只剩下那些普遍成立的特征，既然每个特征都对应一个参数，那么我们减少特征或者降低特征权重，就是让参数等于0或接近0。最原始的想法就是用L0范数，因为它表示向量中非零元素的个数，只要把这个控制在一定范围内，模型复杂度就控制住了。但L0不好求解，因为是NP完全问题，因此求意义接近的L1范数，表示所有参数的绝对值之和。但是L1范数会把一些特征丢弃，但是大家只想让它们在最小化结构风险的过程中尽可能小，所以就有了L2范数来进行规则化。
具体的问题我们接下来慢慢讨论。
2、 为什么说正则相当于加入先验？
那如果我们有了先验知识呢？规则化就是帮助我们加入先验知识到学习过程中的。先说个结论：L1正则就是加入拉普拉斯先验，L2正则就是加入高斯先验，这个先验是针对参数来说的。
下面的内容是从知乎上（https://www.zhihu.com/question/23536142 这个回答下Charles Xiao和Thaurun的回答）学到的，算是自己做的笔记，这些博主的博客也有一些很棒的其他文章，可以学习一下~
规则化=加入先验信息这个是从贝叶斯的角度来看的，如果我们考虑一个线性模型，那么其模型公式为：
这里的 ϵ \epsilon ϵ是白噪声，用来模拟数据集中的观测值 Y ^ \hat Y Y^与真实值之间的误差。因此，我们能够从样本 X X X中预测出真实值 Y Y Y的概率是由白噪声的概率分布决定的。既然是白噪声，那就是符合标准正态分布的，即它的分布为 ϵ \epsilon ϵ~ N ( 0 , δ 2 ) N(0,\delta^2) N(0,δ2)，那么我们能计算得真实值的概率分布也能得到了，仍然符合高斯分布，但是均值会改变： Y i Y_i Yi ~ N ( f ( x i ) , δ 2 ) N(f(x_i), \delta^2) N(f(xi),δ2)，表达式如下：
假设样本之间是独立的，那么我们最后得到的整体预测正确的概率为：
根据极大似然估计，我们最后能够尽可能多地预测正确数据，其概率值和参数 θ \theta θ有关，那么我们的目标就是找到使式(1.3)概率最大的 θ \theta θ值，对其取log也成立：
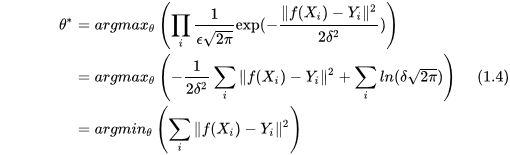
第二个等式就是对第一个取log之后的结果，这个结果中的第二项是常数，在优化过程中是可以忽略不计的，第一项的系数也可以忽略不计，并且加负号后转换成求最小值，优化目标依然成立，但这个形式就已经是最小二乘的形式了，也是我们平时所见到的RMSE损失函数。
到了这一步我们可以看出来，正则就是在最后一个等式的结果上加了一项，对L1规则化往回推导，那就是在似然函数上乘上以下这一项：
∏ exp ( λ ∣ θ i ∣ ) \prod \exp(\lambda |\theta_i|) ∏exp(λ∣θi∣)
L2规则化往回推导，就是在似然函数乘上这一项：
∏ exp ( λ ∣ ∣ θ i ∣ ∣ 2 ) \prod \exp(\lambda ||\theta_i||^2) ∏exp(λ∣∣θi∣∣2)
这两项的形式正好一个接近拉普拉斯分布，一个接近高斯分布。下面还是顺着来看吧。在不考虑 θ \theta θ的分布时，我们认为它的分布是个常数，既然现在知道了，那么极大似然估计的最大化后验概率中必然要乘上这一项：
拉普拉斯分布的概率密度函数：
我们可以认为 λ = 1 b \lambda=\frac{1}{b} λ=b1， μ = 0 \mu = 0 μ=0，这就很接近我们刚才反推的结果了，最后把这个概率值乘上式（1.3）后再简化，结果如下：
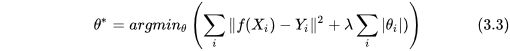
同理，高斯分布的概率密度函数中，取 μ = 0 \mu =0 μ=0, λ = 1 2 δ 2 \lambda=\frac{1}{2\delta^2} λ=2δ21。
3、 为什么L1稀疏L2平滑？
从上面两个概率公式中能看出些苗头，首先，拉普拉斯分布图是这样的：
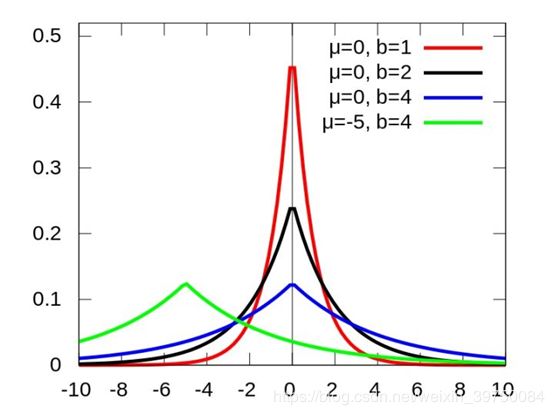
高斯分布的概率分布图是这样的：
我们之前已经讨论过了，我们加入的正则是假设参数分布的均值为0，并且把 λ \lambda λ做了等价， λ \lambda λ越大，表示拉普拉斯分布的 b b b和高斯分布的 δ 2 \delta^2 δ2越小，也就是方差越小，分布越集中在0附近，因此惩罚因子 λ \lambda λ越大，两种规则化的结果必然是越来越多的参数接近0，那为什么我们又会说，L1稀疏，L2平滑呢？
这个从导数上能窥得一二。先写出L1正则的结构风险导数，L1表示加了L1正则后的结构化风险，L表示规则化以前的结构化风险：
∂ L 1 ∂ θ = ∂ L ∂ θ + λ s i g n ( θ ) \frac{\partial L1}{\partial \theta}= \frac{\partial L}{\partial \theta}+ \lambda sign(\theta) ∂θ∂L1=∂θ∂L+λsign(θ)
∂ L 1 ∂ θ = { ∂ L ∂ θ + λ , if θ > 0 ∂ L ∂ θ − λ , if θ < 0 \frac{\partial L1}{\partial \theta}= \begin{cases} \frac{\partial L}{\partial \theta} + {\lambda}, & \text {if $\theta>0$}\\ \frac{\partial L}{\partial \theta} - {\lambda}, & \text {if $\theta<0$} \end{cases} ∂θ∂L1={∂θ∂L+λ,∂θ∂L−λ,if θ>0if θ<0
什么时候 θ = 0 \theta=0 θ=0会是我们要找的极小值点呢？看以下这幅图：
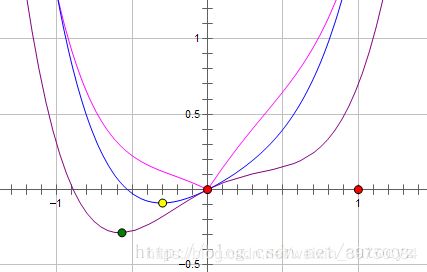
最下方的线是规则化之前的结构化风险函数，中间的是L2规则化的，最上面的是L1规则化的，图片来自于（https://www.zhihu.com/question/37096933王赟 Maigo） 的回答。图中的绿色、黄色、红色的点分别表示这三种函数的极小值点。从图中我们可以看出，只有L1正则的极小值点是在参数为0的位置的，那么这个函数的特点自然是左右两边的导数正好是 θ > 0 \theta>0 θ>0时导数大于0，单调递增， θ < 0 \theta<0 θ<0时导数小于0，单调递减，从这一点启发，我们就可以重新回去看那个公式了，想要在 θ = 0 \theta=0 θ=0处获得最小值，需要：
∂ L ∂ θ + λ > 0 \frac{\partial L}{\partial \theta}+\lambda>0 ∂θ∂L+λ>0
且 ∂ L ∂ θ − λ < 0 \frac{\partial L}{\partial \theta}-\lambda<0 ∂θ∂L−λ<0
结合以上两个式子我们得出，只要在 θ = 0 \theta=0 θ=0的位置满足 λ > ∣ ∂ L ∂ θ ∣ \lambda>|\frac{\partial L}{\partial \theta}| λ>∣∂θ∂L∣，我们就能获得图中粉色线的结果，在 θ = 0 \theta=0 θ=0的位置获得极小值。
那么L2正则呢？先看看导数：
∂ L 2 ∂ θ = ∂ L ∂ θ + 2 λ θ \frac{\partial L2}{\partial \theta}= \frac{\partial L}{\partial \theta}+ 2\lambda \theta ∂θ∂L2=∂θ∂L+2λθ
很容易发现，当 θ = 0 \theta=0 θ=0的时候，L2的导数就是原来L的导数，所以原来的极小值不在 θ = 0 \theta=0 θ=0的位置，那么L2规则化之后的也不会在这个位置。这就解释了为什么L1稀疏而L2不稀疏。
4、 直观解释
下面要放那张被诟病面试时被问死了的图了，如下：
参考了（https://www.zhihu.com/question/37096933 这个问题下王小明的回答）。这里只考虑了两个参数的情况，等高线是怎么画出来的我在逻辑回归的详解里写过了，本质就是所有样本点的损失函数构成的代价函数是一个抛物面（两个参数的情况下），这个抛物面的损失值取不同值的时候其在参数平面的投影就是这个等高线图。
具体分析时，为什么可以把结构化风险函数拆分成两部分？因为在优化里 
和 
是等价的问题。那么通过 E R ( ω ) < = η E_R(\omega)<=\eta ER(ω)<=η，我们也可以很清楚地知道圆和菱形是怎么来的了，因为你限制了它们小于等于一个常数，那么 ∣ ω 1 ∣ + ∣ ω 2 ∣ < = η |\omega_1|+|\omega_2|<=\eta ∣ω1∣+∣ω2∣<=η可不就是个菱形么？ ω 1 2 + ω 2 2 < = η \omega_1^2+\omega_2^2<=\eta ω12+ω22<=η可不就是个圆么？也就是说我们原来要找的极小值点就是蓝色等高线的最中心点，而现在我们需要在黄色区域内寻找在尽可能靠近等高线中心点的值。 λ \lambda λ越大， η \eta η越小（这个数学解释并不清楚，我只能直观地理解它是为了满足整体最小的约束），那么黄色区域面积越小，等高线上获得的极小值会越大，与原来的解相差越多，规则化作用也就越明显。反之，如果 λ \lambda λ非常小，那么黄色区域会非常大，大到包含原始中心点时，规则化就不起任何作用了。
5、 参考资料
1、https://www.zhihu.com/question/37096933/answer/70507353
2、https://blog.csdn.net/red_stone1/article/details/80755144
3、https://www.zhihu.com/question/23536142
4、https://www.zhihu.com/question/47375421
5、https://www.zhihu.com/question/20924039
6、http://charleshm.github.io/2016/03/Regularized-Regression/