使用Python+Pandas+Statsmodels建立线性回归模型预测房价

【综述】

本文通过使用Python+Pandas+Statsmodels建立简单一元线性回归模型、多元线性回归模型来预测房价。

主要内容来源自网页：https://www.learndatasci.com/tutorials/predicting-housing-prices-linear-regression-using-python-pandas-statsmodels/

我在原文基础上增加了大量知识点的说明及解释，以达到学习线性回归的效果。

数据来源：https://github.com/LearnDataSci/article-resources/tree/master/Housing%20Price%20Index%20Regression

目录

1 什么是线性回归？

2 数据集说明

3 变量选择

4 导入分析所用工具包

5 用Pandas读取数据

5.1 读取数据

5.2 了解数据

5.3 数据整理

6 探索性分析

7 最小二乘法

8 简单线性回归

8.1 回归模型

8.2 建模

8.3 结果分析

8.4 线性回归图像

8.4.1 关于自变量的线性回归图像

8.4.2 置信区间

9 多元线性回归 

9.1 回归模型

9.2 建模

9.3 结果分析

9.4 偏回归图

10 总结

---

 

 

1 什么是线性回归？

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

在回归术语中，我们将被预测的变量称为因变量(dependent variable)，用y表示。把用来预测应变量值的一个或多个变量称为自变量（predictor variable/independent variable），用x表示。

2 数据集说明

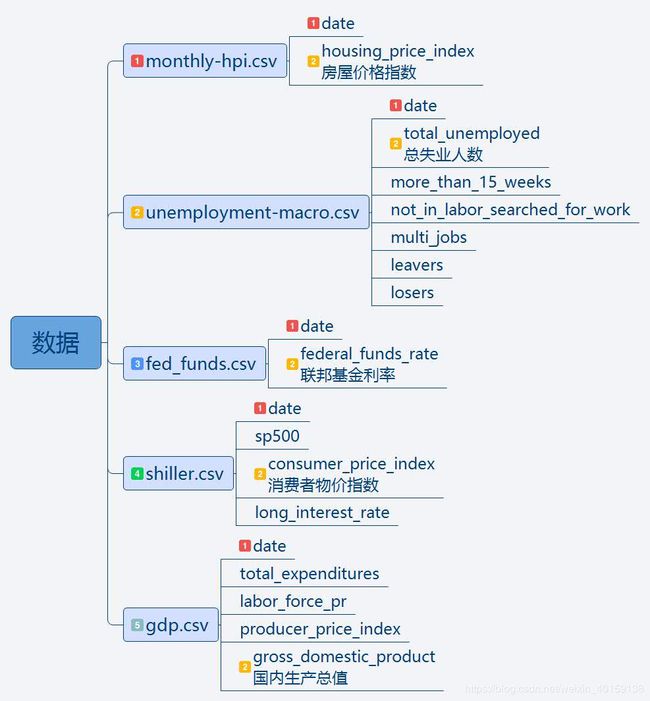
本文用于分析的样本数据集主要有下图中5个csv文件：monthly-hpi.csv，unemployment-macro.csv，fed_funds.csv，shiller.csv，gdp.csv。

每个数据表内的数据列也罗列了出来，可以看到：每张表中都有“date”列，每张表中用于多元线性分析的自变量也用数字2进行了标注。

3 变量选择

【因变量】 我们选择housing_price_index(HPI)作为因变量，该变量度量了住宅房屋的价格变化。

【自变量】我们选择了影响宏观经济的相关因素，比如失业人数、利率、国内生产总值、消费者物价指数。

关于我们选择的自变量的解释，包括他们分别如何影响着房屋价格，以及本文使用的数据源，请参见文章开头给出的Github网址。

4 导入分析所用工具包

import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.sandbox.regression.predstd import wls_prediction_std

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set_style("darkgrid")

import pandas as pd
import numpy as np

5 用Pandas读取数据

5.1 读取数据

你可以直接从Github导入数据，本文选择直接下载到本地后导入。

housing_price_index = pd.read_csv("monthly-hpi.csv")
umemployment = pd.read_csv("unemployment-macro.csv")
federal_funds_rate = pd.read_csv("fed_funds.csv")
shiller = pd.read_csv("shiller.csv")
gross_domestic_product = pd.read_csv("gdp.csv")

5.2 了解数据

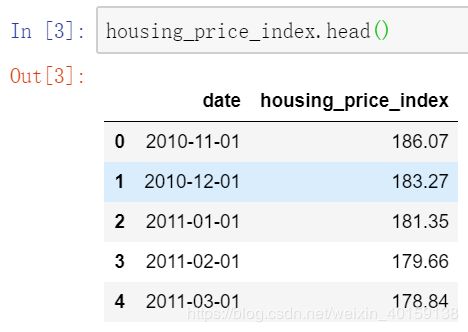
查看数据表的内容及信息，我们以housing_price_index数据框为例：

housing_price_index.head()   # 罗列表格前5行数据

housing_price_index.info()  #参看表格信息

通过逐一了解各个表格的数据信息和info信息，了解到：

housing_price_index    RangeIndex: 73 entries, 0 to 72

umemployment    RangeIndex: 74 entries, 0 to 73

federal_funds_rate    RangeIndex: 74 entries, 0 to 73

shiller    RangeIndex: 70 entries, 0 to 69

gross_domestic_product    RangeIndex: 24 entries, 0 to 23

 其中，gross_domestic_product数据条数少。而且，除了gross_domestic_product中的date日期列按季度时间记录，其他数据中的date日期按照每月记录。

5.3 数据整理

我们现在已经成功导入了数据，使用Pandas的merge函数，将所有表格合并为一张总表格，以便数据分析。

5.2节中提及的时间按月，按季度记录方式不同的问题不需要担心，合并后的数据每一行每一列的数据都符合逻辑，可以满足计算目的。本示例中，最好的是按照共有的date列进行合并，得到的数据是按照季度date保留的数据。

# 按date列合并表格
df = (shiller.merge(housing_price_index,on='date')
            .merge(umemployment,on='date')
            .merge(federal_funds_rate,on='date')
            .merge(gross_domestic_product,on='date'))
df.head()

# df.to_csv("./merge.csv") 如果想将合并后表格导出，可以执行该行代码

合并后的数据前5行截图如下：

查看合并后数据框df主要信息，共得到23条非空数据。

df.info()

6 探索性分析

通常，数据规整之后，我们将进行探索性分析。探索性分析是指对已有数据通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法，可以得出预测因变量最佳的自变量。

为了直接进入主题，本文中略过探索性分析的过程。但是，请铭记在心，探索性分析具有很重要的意义。在现实应用中，直接跳过探索性分析，会影响预测的过程和效果。

7 最小二乘法

本文使用最小二乘法来建模，它是很基础、很强大的方法，应用非常广泛。

最小二乘法通过使得因变量观测值与因变量估计值之间的残差平方和达到最小的方法，得到估计的回归方程。最小二乘准则就是选择能与样本数据有最佳拟合方程的准则。

最小二乘法建立在假定之上，如果假设成立，建立的模型可以用来较准确地预测数据。反之，假设不成立，模型论断将失去其有效性。

最小二乘法假定：

1）线性关系：假定因变量与自变量之间存在线性关系。如果不存在线性关系，线性回归不是解释数据的正确模型。

2）无多重共线性：因变量之间不存在相关性。如果某些因变量之间存在密切联系，可以尝试删去其中一个或多个相关的因变量。因为多余的因变量提供了冗余信息，剔除多余变量并不会大大降低修正判定系数。

3）零条件均值假定：观测值和线性拟合估计值之间的平均残差为0。有时候观测值和估计值相比，偏大；有时候偏小，但之间的残差不会无控制地偏向于一群值。

4）同方差：对于自变量的不同取值，因变量的误差项都是独立的，方差是相同的。

5）无自相关性/序列相关：自相关是指一个变量同自身其他观测值有相互关系。比如，如果今天的股票价格影响着明天的股票价格，那么股票价格就是序列相关的。

8 简单线性回归

8.1 回归模型

简单线性回归使用一个自变量来预测一个因变量，二者之间的关系可以用一条直线近似表示。

简单线性回归模型：

其中：

y = 因变量

β = 回归系数

α = 截距 （自变量为0时，因变量房价的平均值/期望）

x = 用于预测y的自变量

 = 随机变量，称为模型误差项，说明在y里面但不能被x和y之间线性关系解释的变异性

8.2 建模

我们将使用statsmodels中ols功能，构建housing_price_index同total_unemployed之间的模型。

 Statsmodels是一个很强大的Python库，用于拟合多种统计模型，执行统计测试以及数据探索和可视化。

对于线性回归linear regression，我们可以使用Statsmodels库中最小二乘法OLS（Ordinary-Least-Square）的功能来实现，可以得到丰富的数据信息。

# 构建模型
housing_model = ols("housing_price_index ~ total_unemployed",data=df).fit()
housing_model_summary = housing_model.summary()
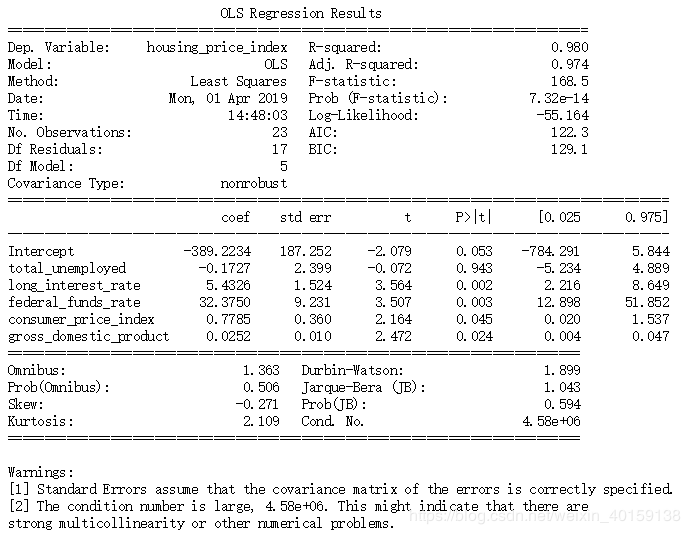
print(housing_model_summary)

结果如下：

8.3 结果分析

1） 修正判定系统Adj.R-squared：94.9%。房屋价格指数变异性的94.9%能被其与失业人数之间的线性关系解释。

2）回归系数：-8.3324。代表失业人数每增加一个单位，房屋价格指数将降低8.33。和我们常识理解的想法一致，失业人数增加，房屋价格会下降。

3）回归系数的标准误差stand error：0.410，即β的估计的标准差。通过不同的失业人数数据，可以计算得到回归系统的标准误差。回归系数标准误差，是量度结果精密度的指标。这里计算得出的标准误差为0.41，数值很小，说明精确度还是不错的。

回归系统β的标准误差的说明：

对于观测数据{（，），i = 1,2,...,n}，我们这样描述其关系 

，该式中分子其实就是均方误差MSE。

（有兴趣的同学，可以导出合并后数据自行计算下，通过上面的公式，可以得到 = 0.410）

4）p-值为0%。根据简单线性回归显著性的t检验，原假设housing_price_index同total_unemployed之间不存在线性关系，β为0。

而现在p值为0%，小于显著性水平0.05。所以拒绝原假设，β显著不等于0。我们足以断定，housing_price_index同total_unemployed之间存在一个显著的关系。

5）β的95%的置信区间：-9.185 ~ -7.48。我们有95%的信心，回归系数β将落在置信区间 [-9.185, -7.480]中。换个角度来讲，简单线性回归显著性的t检验，假设β为0，而β=0并没有包含在上述置信区间内，所以我们可以拒绝原假设，断定housing_price_index同total_unemployed之间存在一个显著的关系。

8.4 线性回归图像

8.4.1 关于自变量的线性回归图像

fig = plt.figure(figsize=(15,8))

fig = sm.graphics.plot_regress_exog(housing_model,"total_unemployed", fig =fig)

fig.savefig('./simple linear regression plots.jpg',dpi=300) #保存图片

我们得到下述图像：

图像说明：

1）左上一图 “Y and Fitted vs. X” ，刻画了房价观测值同线性回归模型拟合的估计值之间的差距。同时，可以发现二者是负相关的，斜率β为负。

2）右上一图 “Residuals versus total_unemployed”为 关于自变量total_unemployed的残差图。横坐标为自变量total_unemployed的值，纵轴表示自变量对应的残差值，也就是左上一图中蓝圆点同橘色菱形间的距离差。

残差图是用来评价回归模型假定有效性的一种方法。通过这张残差图，总体印象为所有的散点都在±7.5范围的水平带中间，我们有信心做出结论，简单线性回归模型是合理的。 

3）左下一图“Partial regression plot”偏回归图像显示考虑新增其他自变量时，房价指数与总失业人数之间的关系。我们会在后续多元线性回归环节，看到增加更多的自变量后同样的图像将产生怎样的变化。

4）右下二图“component and component-plus-residual（CCPR）”图像是偏回归图像的拓展，反映了考虑新增其他自变量后反应两者关系的直线将如何变化。

8.4.2 置信区间

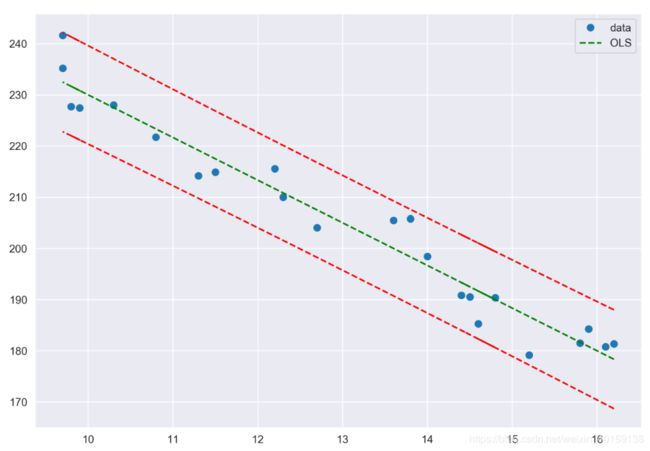
下面我们做图画出拟合线（绿色标记），样本数据中的观测值（蓝色圆点），置信区间（红色标记）。

# x为自变量，y为因变量
x = df[["total_unemployed"]]
y = df[["housing_price_index"]]   # 注意单个方括号为series，两个方括号为dataframe


# 获取置信区间
# wls_prediction_std(housing_model)返回三个值,标准差，置信区间下限，置信区间上限
# 标准差我们这里用不到，用 _ 表示一个虚拟变量占个位

_,confidence_interval_lower,confidence_interval_upper = wls_prediction_std(housing_model)

fig, ax =plt.subplots(figsize=(10,7))


# 'o' 代表圆形, 也可以使用 'd'(diamonds菱形),'s'(squares正方形)
ax.plot(x,y,'o',label="data")

# 画拟合线，g-- 代表绿色
ax.plot(x,housing_model.fittedvalues,"g--",label="OLS")

# 画出置信区间 r-- 代表红色
ax.plot(x,confidence_interval_upper,"r--")
ax.plot(x,confidence_interval_lower,"r--")

# 显示图例
ax.legend(loc="best")

# 导出图片保存
fig.savefig('./confidence interval.jpg',dpi=300)

结果为：

9 多元线性回归 

9.1 回归模型

多元线性回归模型为：   

我们知道仅仅考虑失业人数是不能完全解释房屋价格的。为了更加准确地分析是什么影响着房价，我们引入一些不同的自变量来分析，看看哪些自变量的组合更优地满足OLS最小二乘假定。这里新增的自变量从经济层面因素引入。

参照第2节中数据集说明，本文多元线性回归模型考虑的自变量有：新增的federal_funds_rate，long_interest_rate，consumer_price_index，gross_domestic_product，还有之前的自变量：total_unemployed。

9.2 建模

housing_model = ols("""housing_price_index ~ total_unemployed
                                            + long_interest_rate
                                            + federal_funds_rate
                                            + consumer_price_index
                                            + gross_domestic_product""",data=df).fit()

housing_model_summary = housing_model.summary()
print(housing_model_summary)

结果为：

9.3 结果分析

1） 修正判定系统Adj.R-squared从之前的94.9%上升到97.4%。房屋价格指数变异性的97.4%能被其与多个自变量之间的线性关系解释。

2）回归系数coef：通过回归系数，可以发现，只有当总失业人数对应的回归系数为负，表示当其增加时，房价降低；其他自变量的回归系数为正，表示当其所代表的消费水平、利率上涨时，房价上涨，这也符合我们的常识理解。

3）total_unemployed自变量的standard error从0.410变为2.399，p-value从原来的0变为0.943，没有通过t检验。数据的变化表明因为新增自变量的加入，降低了失业情况对房价的影响，失业情况在此模型中对房价的影响明显减弱了。

4）虽然total_unemployed和房价指数housing_price_index是有关系的，但其他自变量所代表的因素更能影响着房价的变化。现实世界各变化因素互联互通，相互影响，不是简单的线性回归模型能概括的，需要更全面的模型来解释。这也是多元线性回归模型大大地改变之前简单线性回归模型结论的原因。

5）新引入的自变量的p值都小于显著性水平5%，说明这些自变量同房屋价格指数是有显著关系的。考虑到判定系数的增加，更加说明多元线性回归模型在这里是优于简单一元线性回归的。

9.4 偏回归图

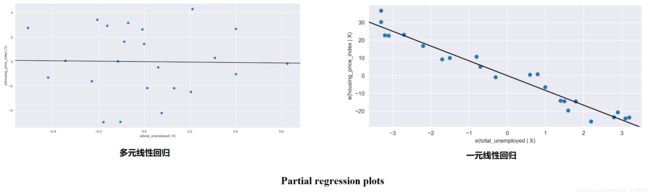
partial regression plot 偏回归图，是呈现了模型中已有一个或多个自变量的情况下，新增一个自变量对模型产生的影响。

本小节绘制partial regression plot 偏回归图，来看看total_unemployed的作用是如何被其他自变量影响了。

fig = plt.figure(figsize=(25,18))
fig = sm.graphics.plot_partregress_grid(housing_model,fig=fig)

fig.savefig('./partial regression plots.jpg',dpi=300)

运行生成如下图像：

 

右上一图为关于total_unemployed的偏回归图，我们将简单一元线性回归中的偏回归图拿出进行两者的对比：

可以很明显地看出，加入多个自变量后， 多元线性回归中关于total_unemployed的偏回归图已经没有明显的趋势变化。这表明在这个模型中，total_unemployed对housing_price_index产生的影响很小，对housing_price_index的变异性不具有解释性了。

而其他自变量对应的图像有明显的趋势变化，这也说明这些变量对housing_price_index的影响力更强。这也再次验证了，federal_funds_rate，consumer_price_index，long_interest_rate，gross_domestic_product 能更好地解释housing_price_index。多元线性回归模型拟合的效果优于简单线性回归。

10 总结

本文中，我们操作了如果构建简单线性回归、多元线性回归模型来预测房价，考虑了宏观经济层面的一些指标，同时对模型描述信息进行分析，能简单评估线性回归模型的拟合质量。

坦白来讲，解释房价是很困难的问题，现实生活中，有大量的预测变量可以用来预测房价。同时，房价也会对这些预测变量产生影响。更复杂地，是这些因素和变量一一相互影响着。

作为房价预测所用的模型和方法，本文存在很多的不足，包括：

1）本文选用了一些宏观经济层面的变量，通过线性回归模型来预测房价。但，其实有更大的空间去完善模型，寻找比线性回归更合适的模型，也可以考虑选择其他更优的变量。

2）本文使用的数据集仅仅是容量很小的数据集，而建模预测房价这复杂的问题，通常需要六年以上的数据。另外，我们使用的数据，偏向于房地产危机事件之后的数据，不能代表和反应房地产市场的长期趋势。

3） 细心的人会注意到多元线性回归模型中，描述信息截图中关于多重共线性产生的警告。我们有两个或两个以上变量对房价产生相同的影响，这使得这些自变量的作用被夸大。

4）若自变量的过去影响其当前和未来的情况，我们称为自相关。其实，自相关的情况也是存在于我们的模型中的。

 

本文主要的目的，是通过这个例子，学习和了解建模的过程，测试、分析、失败后不断尝试。大家可以尝试挖掘数据，对这个模型中的自变量进行不同的删减组合，来看看对OLS拟合效果的影响。

如您对本文内容有任何意见，欢迎留言交流~！