机器学习：神经网络代价函数总结

神经网络代价函数

---

1. 代价函数基本定义

• 代价函数是衡量模型预测输出值与目标真实值之间差距的一类函数，在一些场景中也称为目标函数。
• 在神经网络中，代价函数(如二次误差函数)衡量输出值与真实值之间的误差，以此进行误差反向传递，不断调整网络中权值和阈值，从而使得预测值和真实值之间的差距越来越小。
• 一些常用的代价函数主要有：二次代价函数、交叉熵代价函数以及对数似然函数等等。

---

2. 二次代价函数

• 定义

考虑 n n 个样本的输入 z1,z2,...zn z 1 , z 2 , . . . z n ，对应的真实值为 y1,y2,...,yn y 1 , y 2 , . . . , y n ，对应的输出为 o(zi) o ( z i ) ，则二次代价函数可定义为：

C=12n∑i=1n||yi−o(zi)||2 C = 1 2 n ∑ i = 1 n | | y i − o ( z i ) | | 2

其中， C C 表示代价函数， n n 表示样本总数。

• 以一个样本为例

假设在神经网络中，上一层每个神经元的输出为 xj x j ，权值为 wj w j ，偏置值为 b b 。当前输出神经元的激活函数为 σ(⋅) σ ( ⋅ ) 。则该神经元的输入值为 z=∑wjxj+b z = ∑ w j x j + b ，此时二次代价函数为：

C=(y−σ(z))22 C = ( y − σ ( z ) ) 2 2

其中， y y 为真实值。

• 考虑权值和偏置值更新

假如使用梯度下降法(Gradient descent)来调整权值和偏置值大小，则对 w w 和 b b 求偏导得：

∂C∂w=(σ(z)−y)σ′(z)x∂C∂w=(σ(z)−y)σ′(z) ∂ C ∂ w = ( σ ( z ) − y ) σ ′ ( z ) x ∂ C ∂ w = ( σ ( z ) − y ) σ ′ ( z )

该偏导数乘以学习率 l l 就变成了每次调整权值和偏置值得步长。当 l l 一定时，可以看出 w w 和 b b 的梯度跟激活函数的梯度成正比，激活函数的梯度（导数）越大，则 w w 和 b b 调整得就越快，训练收敛得就越快。

• 结合激活函数

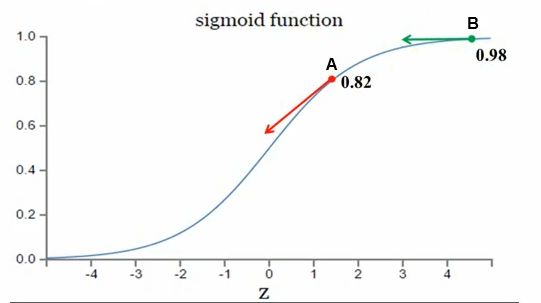
假设神经元使用的激活函数为sigmoid函数，如下图所示：

• 考虑 A A 点和 B B 点，权值调整大小与sigmoid函数的梯度（导数）有关。
• 当真实值 y=1 y = 1 时，则输出值目标是收敛至 1 1 。 A A 离目标比较远，权值调整大； B B 离目标比较近，权值调整小。调整方案合理。

• 当真实值 y=0 y = 0 时，则输出值目标是收敛至 0 0 。 A A 离目标比较近，权值调整大； B B 离目标比较远，权值调整小。调整方案不合理。换句话说，很难调整到目标值 0 0 。

• 结论

可以看出，二次代价函数在使用sigmoid或tanh的s型激活函数时，在收敛至 0 0 时，存在收敛速度慢而导致的训练速度慢的问题。

---

2. 交叉熵代价函数

• 交叉熵

在分析交叉熵代价函数函数之前，先来了解一下交叉熵的概念。

首先引入信息熵，给定一个随机变量 X=x1,x2,...,xn X = x 1 , x 2 , . . . , x n ，对应的概率分布为 p1,p2,...pn p 1 , p 2 , . . . p n ，则信息熵就是用来衡量随机变量的不确定性大小，定义为：

H(X)=∑i=1npilog21pi H ( X ) = ∑ i = 1 n p i log 2 ⁡ 1 p i

消除随机变量不确定性大小的 最小代价即是该跟据随机变量 真实分布计算的信息熵大小。
而 交叉熵就是用来衡量在给定的真实分布下，使用 非真实分布所指定的策略 消除系统的不确定性所需要付出的努力的大小。
假设得到随机变量的非真实分布为 q1,q2,...,qn q 1 , q 2 , . . . , q n
则计算 交叉熵为：

cross_entropy=H(p,q)=∑i=1npilog21qi c r o s s _ e n t r o p y = H ( p , q ) = ∑ i = 1 n p i log 2 ⁡ 1 q i

交叉熵越低，表示策略就越好，最低的交叉熵也就是使用了真实分布所计算出来的信息熵。此时 ，交叉熵 = 信息熵。

• 交叉熵代价函数定义

考虑 n n 个样本的输入 z1,z2,...zn z 1 , z 2 , . . . z n ，对应的真实值为 y1,y2,...,yn y 1 , y 2 , . . . , y n ，对应的输出为 oi o i ，则交叉熵代价函数可定义为：

C=−1n∑i=1n[yilnoi+(1−yi)ln(1−oi)] C = − 1 n ∑ i = 1 n [ y i ln ⁡ o i + ( 1 − y i ) ln ⁡ ( 1 − o i ) ]

其中， C C 表示代价函数， n n 表示样本总数。

• 结合激活函数考虑

假设在神经网络中，上一层每个神经元的输出为 xi x i ，权值为 wi w i ，偏置值为 b b 。当前输出神经元的激活函数为 σ(⋅) σ ( ⋅ ) 。则每个神经元的输入值为 z=∑wixi+b z = ∑ w i x i + b ，此时考虑 n n 个神经元，交叉熵代价函数为：

C=−1n∑i=1n[yiln(σ(z))+(1−yi)ln(1−σ(z))] C = − 1 n ∑ i = 1 n [ y i ln ⁡ ( σ ( z ) ) + ( 1 − y i ) ln ⁡ ( 1 − σ ( z ) ) ]

其中， yi y i 为真实值，

• 考虑权值和偏置值更新

对比二次代价函数，同样选择sigmoid激活函数，则 σ′(z)=σ(z)(1−σ(z)) σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) )

则权值 w w 的梯度(更新步长)为：

∂C∂wi=−1n∑i=1n(yiσ(z)−(1−yi)1−σ(z))∂σ∂wi=−1n∑i=1n(yiσ(z)−(1−yi)1−σ(z))σ′(z)xi=1n∑i=1nσ′(z)xiσ(z)(1−σ(z))(σ(z)−yi)=1n∑i=1nxi(σ(z)−yi) ∂ C ∂ w i = − 1 n ∑ i = 1 n ( y i σ ( z ) − ( 1 − y i ) 1 − σ ( z ) ) ∂ σ ∂ w i = − 1 n ∑ i = 1 n ( y i σ ( z ) − ( 1 − y i ) 1 − σ ( z ) ) σ ′ ( z ) x i = 1 n ∑ i = 1 n σ ′ ( z ) x i σ ( z ) ( 1 − σ ( z ) ) ( σ ( z ) − y i ) = 1 n ∑ i = 1 n x i ( σ ( z ) − y i )

同理，偏置值 b b 的梯度(更新步长)为：

∂C∂b=1n∑i=1n(σ(z)−yi) ∂ C ∂ b = 1 n ∑ i = 1 n ( σ ( z ) − y i )

可以看出，权值和偏置值的调整与 σ′(z) σ ′ ( z ) 无关，而与 σ(z) σ ( z ) 有关。此外， σ(z)−y σ ( z ) − y 表示真实值与输出值之间的误差。当误差越大时，梯度就越大， w w 和 b b 的调整就越快，训练速度就越快。

• 结论：

对比二次代价函数可以发现，代价函数的选择与激活函数有关。当输出神经元的激活函数是线性时例如，ReLU函数）二次代价函数是一种合适的选择；当输出神经元的激活函数是S型函数（例如sigmoid、tanh函数）时，选择交叉熵代价函数则比较合理。

---

3. 对数似然函数代价函数

• 定义：

考虑 n n 个样本的输入 z1,z2,...zn z 1 , z 2 , . . . z n ，对应的真实值为 y1,y2,...,yn y 1 , y 2 , . . . , y n 取值为 0 0 或 1 1 ，对应的第 i i 个神经元输出为 oi o i ，则对数 log log 似然代价函数可定义为：

C=−∑i=1nyilogoi C = − ∑ i = 1 n y i log ⁡ o i

其中， C C 表示代价函数， n n 表示样本总数。

在深度学习中，对数似然函数常用来搭配softmax激活函数使用。

• 考虑softmax激活函数

假定神经网络的每个输出层神经元（假设共 n n 个）都使用softmax激活函数：

oj=ezj∑kezk o j = e z j ∑ k e z k

其中， zj z j 表示输出层第 j j 个神经元的输入， oj o j 表示第 j j 输出神经元的输出。 ∑kezk ∑ k e z k 表示所有输出层神经元的输入之和。

softmax函数的特点在于：

• 它把每个神经元的输入占当前层所有神经元输入之和的比值，当作该神经元的输出。这使得输出更容易被解释：神经元的输出值越大，则该神经元对应的类别是真实类别的可能性更高。
• 此外，softmax的输出是一个归一化的概率分布，能够衡量输出分布与真实分布之间的差距。

softmax函数求导：

分两种情况：

• j=i j = i 时：
  ∂oj∂zi=∂∂zi(ezj∑kezk)=(ezj)′⋅∑kezk−ezj⋅ezj(∑kezk)2=ezj∑kezk−ezj∑kezk⋅ezj∑kezk=oj(1−oj) ∂ o j ∂ z i = ∂ ∂ z i ( e z j ∑ k e z k ) = ( e z j ) ′ ⋅ ∑ k e z k − e z j ⋅ e z j ( ∑ k e z k ) 2 = e z j ∑ k e z k − e z j ∑ k e z k ⋅ e z j ∑ k e z k = o j ( 1 − o j )
• j≠i j ≠ i 时：
  ∂oj∂zi=∂∂zi(ezj∑kezk)=0⋅∑kezk−ezj⋅ezi(∑kezk)2=−ezj∑kezk⋅ezi∑kezk=−ojoi ∂ o j ∂ z i = ∂ ∂ z i ( e z j ∑ k e z k ) = 0 ⋅ ∑ k e z k − e z j ⋅ e z i ( ∑ k e z k ) 2 = − e z j ∑ k e z k ⋅ e z i ∑ k e z k = − o j o i

求导完毕。

• softmax配合对数似然代价函数

考虑神经网络输出层神经元，对应多分类问题时。 ok o k 表示第 k k 个神经元的输出， yk y k 表示第 k k 个神经元对应的真实值，取值为 0 0 或 1 1 。则总的代价函数为：

C=−∑kyklogok C = − ∑ k y k log ⁡ o k

其中， ok=σ(zj) o k = σ ( z j ) 。其中， σ(⋅) σ ( ⋅ ) 表示softmax激活函数； zj=∑wjkxk+bj z j = ∑ w j k x k + b j 为每个神经元的输入。

• 考虑权值和偏置值的更新

对权值 wjk w j k 求偏导得权值更新步长为：

∂C∂wjk=∂C∂zj⋅∂zj∂wjk=∂C∂zj⋅∂(∑wjkxk+bj)∂wjk=−∑kxkyk∂∂zj(logok)=−∑kxkyk1ok∂ok∂zj(拆分求导)=−xjyj1oj⋅oj(1−oj)−∑k≠jxkyk1ok⋅(−ojok)=−xjyj(1−oj)+oj∑k≠jxkyk(合并)=oj∑xkyk−xjyj   这里, ∑xkyk=xj=xj(oj−yj) ∂ C ∂ w j k = ∂ C ∂ z j ⋅ ∂ z j ∂ w j k = ∂ C ∂ z j ⋅ ∂ ( ∑ w j k x k + b j ) ∂ w j k = − ∑ k x k y k ∂ ∂ z j ( log ⁡ o k ) = − ∑ k x k y k 1 o k ∂ o k ∂ z j ( 拆 分 求 导 ) = − x j y j 1 o j ⋅ o j ( 1 − o j ) − ∑ k ≠ j x k y k 1 o k ⋅ ( − o j o k ) = − x j y j ( 1 − o j ) + o j ∑ k ≠ j x k y k ( 合 并 ) = o j ∑ x k y k − x j y j       这 里 ,   ∑ x k y k = x j = x j ( o j − y j )

上式中， ∑xkyk=xj ∑ x k y k = x j 是由于softmax函数对应多分类真实值时，只能有一项为1（该项最可能为输出神经元 j j 输出值对应的项），其余皆为0。

同理得偏置值更新步长为：

∂C∂bj=oj−yj ∂ C ∂ b j = o j − y j

可以看出，权值和偏置得更新与输出值和真实值之间得误差有关，误差越大，权值和偏置更新得速度越快，训练得速度也就越快。

• 总结：

根据上述分析可得，对数似然代价函数配合softmax函数和交叉熵代价函数配合S型函数的原理相似，都能有效地解决权值和偏置值更新速度慢导致得训练速度慢的问题。二者联系：对数似然代价函数在二分类时，可以简化为交叉熵代价函数的形式。

• 扩展：

在Tensorflow中：

tf.nn.sigmoid_cross_entropy_with_logits() # 表示sigmoid搭配使用交叉熵。
tf.nn.softmax_cross_entropy_with_logits() # 表示softmax搭配使用的交叉熵。

---

参考资料

讲师Ben: 炼数成金课程——深度学习框架Tensorflow学习与应用
softmax的log似然代价函数（公式求导）