【论文笔记】Deep Metric Learning via Facility Location
Deep Metric Learning via Facility Location论文笔记
2017 CVPR的,因为end to end 思想,metric learning所以需要学习。
Abstract
基于结构化预测,提出新的度量学习准则,用于优化聚类指标。
Introduction
myopic 目光短浅的。我没见过说别人方法这么狠的
现有方法都没有考虑向量空间中的全局结构,具体看图就了解了。
Related Work
从FaceNet开始讲起,Lifted Structured embedding, N-pairs embedding 以及其他。
其实与本文主要思想没什么太大的关系,metric learning就是metric learning
Methods
主要的一个assumption非常有意思。作者认为在metric learning的时候,光靠传统的一个对比方式可能会出现同类别embedding的偏差较大。如图:
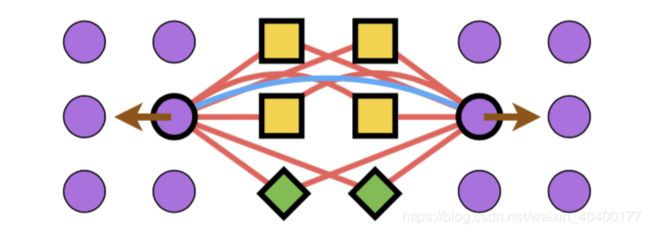
可以看到黄色的方块与绿色的菱形集中在一起。这没什么太大的问题。而由于选取hard或者semi-hard的sample来distance measure并且让二者远离。就可能会使得左右两侧的紫色圆球逐渐的被分离为两个较远的group。这一点很有趣,作者也针对这个提出了对应了的loss,避免这个问题。如下图所示。
3.1 Facility location problem
给定输入为 X i X_i Xi, 转换为embedding方程 f ( X i ; Θ ) f(X_i; \Theta) f(Xi;Θ), 此时需要选取一个子集 S ⊆ V S \subseteq \mathcal{V} S⊆V 其中 V = { 1 , . . . , ∣ X ∣ } \mathcal{V} = \{1, ..., |X|\} V={1,...,∣X∣}。
后半段换成通俗易懂的语言就是我们在 X i X_i Xi个输入中选取一部分作为类别或者聚类中心。
具体的优化方程如下:
F ( X , S ; Θ ) = − ∑ i ∈ ∣ X ∣ min j ∈ S ∥ f ( X i ; Θ ) − f ( X j ; Θ ) ∥ F(X, S ; \Theta)=-\sum_{i \in|X|} \min _{j \in S} \| f\left(X_{i} ; \Theta\right)-f\left(X_{j} ; \Theta\right) \| F(X,S;Θ)=−i∈∣X∣∑j∈Smin∥f(Xi;Θ)−f(Xj;Θ)∥
对每一个输入样例,在类别集合 S S S,选取使样例 X i X_i Xi到类别代表 X j X_j Xj距离最小的。
那么使得这个方程的loss最大,就是最终的优化目标。
笔者注:
此处和原始的Facility location problem 略有不同,general的定义是在图上任意定义中心的位置并且中心的数量增多会使得结果变得糟糕。同时考虑中心数量的同时也考虑每一个最近的点到中心的距离。(若不考虑中心数量,则毫无疑问最优解是每一个点都是中心。)
此处相当于中心仅能能从输入样例中的选取并且不考虑中心的cost。
原问题是个NP-hard的问题,用子模块的贪心算法优化可以使得结果在 O ( 1 − 1 e ) O(1-\frac{1}{e}) O(1−e1)的误差范围内接近最佳。
3.2 Structured facility location for deep metric learning
考虑到上述的优化方程 F F F之后,结合ground truth一起进行训练。
F ~ ( X , y ∗ ; Θ ) = ∑ k ∣ Y ∣ max j ∈ { i : y ∗ [ i ] = k } F ( X { i : y ∗ [ i ] = k } , { j } ; Θ ) \tilde{F}\left(X, \mathbf{y}^{*} ; \Theta\right)=\sum_{k}^{|\mathcal{Y}|} \max _{j \in\left\{i: \mathbf{y}^{*}[i]=k\right\}} F\left(X_{\left\{i: \mathbf{y}^{*}[i]=k\right\}},\{j\} ; \Theta\right) F~(X,y∗;Θ)=k∑∣Y∣j∈{i:y∗[i]=k}maxF(X{i:y∗[i]=k},{j};Θ)
意为对于每一个label k ∈ y k \in \mathcal{y} k∈y, 从所有样例 X X X中取出对应label下的输入 X { i : y ∗ [ i ] = k } X_{\{i: \mathbf{y}^{*}[i]=k\}} X{i:y∗[i]=k},并分别对每一个类别进行maxmize。
作者希望聚类的分数会比最大违反聚类的情况要好。因此定义如下的损失函数:
ℓ ( X , y ∗ ) = [ max S ⊂ V ∣ S ∣ = ∣ Y ∣ { F ( X , S ; Θ ) + γ Δ ( g ( S ) , y ∗ ) } ⏟ ( ∗ ) − F ~ ( X , y ∗ ; Δ ) ] + \ell\left(X, \mathbf{y}^{*}\right)=[\underbrace{\max _{S \subset V \atop|S|=|\mathcal{Y}|}\left\{F(X, S ; \Theta)+\gamma \Delta\left(g(S), \mathbf{y}^{*}\right)\right\}}_{(*)} - \tilde{F}(X, \mathbf{y}^{*}; \Delta)]_+ ℓ(X,y∗)=[(∗) ∣S∣=∣Y∣S⊂Vmax{F(X,S;Θ)+γΔ(g(S),y∗)}−F~(X,y∗;Δ)]+
最大违反聚类的情况这话就说挺离谱的
公式前半部分:模型输入进行metric表征并且得到结果 g ( S ) g(S) g(S)然后与 y ∗ \mathbf{y}^* y∗计算误差(具体为NMI)
后半部分:与最佳的聚类结果进行比较。
并且保证不超过最佳的结果(最后处的加号,使得结果不为正(通过上下文猜的))
这样对模型进行反向传播训练,可以得到不错的结果。
个人总结
主要思想是结合了facility location function,将标准的label融入进行,使用NMI可以用来做反向传播。
metric learning,可以在下游任务clustering中完成的比较好。
此时回头,仔细看本文第二张图,加粗的紫色圆圈代表了答案的聚类中心,并且用浅灰色方框圈了出来。这是FLF的思想,并且使用cluster的标准答案,使得左半部分的紫色圆圈类会尽可能的向右半部分靠拢,从而得出更好的聚类结果。
调研阶段,后面反向传播就暂时不啃了,如果到时候需要用这个方法,应该会过来填坑。
数学还是差了一些。希望大家指正与交流。
