实战技术!OpenGL超级宝典笔记——贝塞尔曲线和曲面
个人博客导航页(点击右侧链接即可打开个人博客):大牛带你入门技术栈
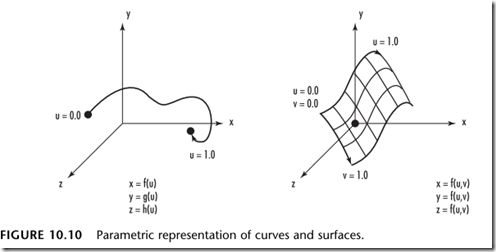
参数方程表现形式
在中学的时候,我们都学习过直线的参数方程:y = kx + b;其中k表示斜率,b表示截距(即与y轴的交点坐标)。类似地,我们也可以用一个参数方程来表示一条曲线。1962年,法国工程师贝塞尔发明了贝塞尔曲线方程。关于贝塞尔曲线的详细介绍可以参考(维基贝塞尔)。这里只介绍OpenGL实现贝塞尔的函数。
OpenGl定义一条曲线时,也把它定义为一个曲线方程。我们把这条曲线的参数成为u,它的值域就是曲线的定义域。曲面则需要u和v两个参数来描述。注意,u和v参数只表示了描述曲线的参数方程的范围,它们并没有反映实际的坐标值。其坐标可以表示为:
x = f(u); y = g(u); z = h(u);
如下图:
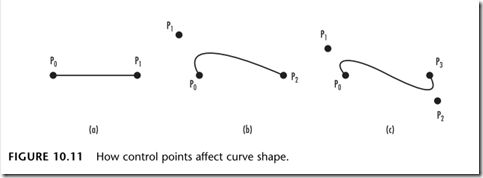
控制点
贝塞尔曲线的形状由控制点来控制。贝塞尔曲线的控制点个数为曲线的阶。根据控制点的个数,贝塞尔曲线又分为二次贝塞尔曲线,三次贝塞尔曲线,高阶贝塞尔曲线。
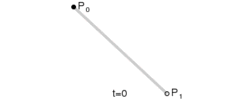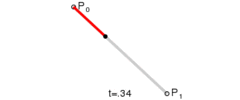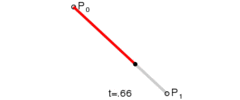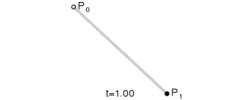
线性曲线
线性贝塞尔曲线演示动画,t in [0,1]
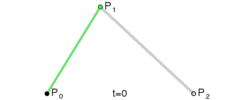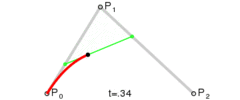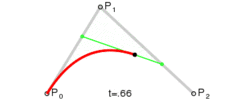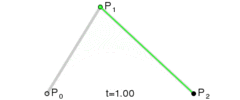
二次方曲线
为建构二次贝塞尔曲线,可以中介点Q0和Q1作为由0至1的t:
-
由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。
-
由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。
-
由Q0至Q1的连续点B(t),描述一条二次贝塞尔曲线。
二次贝塞尔曲线的结构
二次贝塞尔曲线演示动画,t in [0,1]
三次方曲线
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2,和由二次曲线描述的点R0、R1所建构:
三次贝塞尔曲线的结构
三次贝塞尔曲线演示动画,t in [0,1]
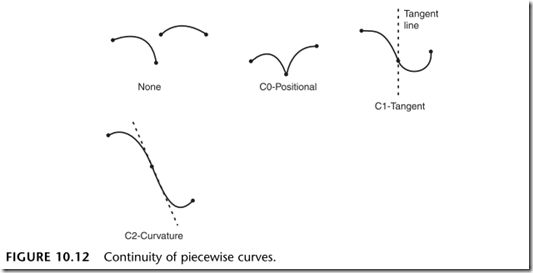
连续性
两段曲线是否相连接,代表这两段曲线是否连续的。曲线的连续性分为4种,无连续,点连续,正切连续,曲率连续。下图分别表示了这几种情况:
其中曲率连续的曲线过渡的更平滑。我们可以通过参数来设置曲线的连续性。
求值器
OpenGL提供了一些函数来绘制贝塞尔曲线和曲面。我们只需要提供控制点和u,v作为参数,然后调用求值函数来绘制曲线。
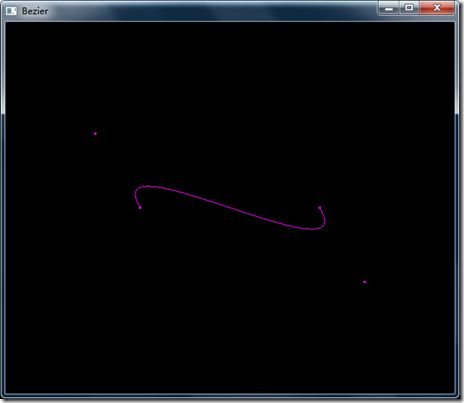
2D曲线的例子:
//控制点 GLint numOfPoints = 4; static GLfloat controlPoints[4][3] = {{-4.0f, 0.0f, 0.0f},
{-6.0f, 4.0f, 0.0f},
{6.0f, -4.0f, 0.0f},
{4.0f, 0.0f, 0.0f}}; void SetupRC()
{
glClearColor(0.0f, 0.0f, 0.0f, 1.0f);
glColor3f(1.0f, 0.0f, 1.0f);
}
//画控制点
void DrawPoints()
{
glPointSize(2.5f);
glBegin(GL_POINTS); for (int i = 0; i < numOfPoints; ++i)
{
glVertex3fv(controlPoints[i]);
}
glEnd();
}
void ChangeSize(GLsizei w, GLsizei h)
{
if (h == 0)
{
h = 1;
}
glViewport(0, 0, w, h);
//使用正交投影
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(-10.0f, 10.0f, -10.0f, 10.0f);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
void RenderScene()
{
glClear(GL_COLOR_BUFFER_BIT);
//设置贝塞尔曲线,这个函数其实只需要调用一次,可以放在SetupRC中设置
glMap1f(GL_MAP1_VERTEX_3, //生成的数据类型
0.0f, //u值的下界
100.0f, //u值的上界
3, //顶点在数据中的间隔,x,y,z所以间隔是3
numOfPoints, //u方向上的阶,即控制点的个数
&controlPoints[0][0] //指向控制点数据的指针 );
//必须在绘制顶点之前开启
glEnable(GL_MAP1_VERTEX_3);
//使用画线的方式来连接点
glBegin(GL_LINE_STRIP);
for (int i = 0; i <= 100; i++)
{
glEvalCoord1f((GLfloat)i);
}
glEnd();
DrawPoints();
glutSwapBuffers();
}
在RenderScene函数中调用glMap1f来为曲线创建映射。第一个参数为GL_MAP1_VERTEX3,设置求值器产生顶点为三元组(x,y,z).还可以设置为产生纹理坐标和颜色信息。参考glMap1.后面的两个参数设定了u的取值范围[0,100],第四个参数指定了顶点在数组中的间隔,由于顶点是由3个浮点数组成,所以间隔是3.第五个参数指定了控制点的个数,最后一个参数是控制点数组。然后我们需要启用求值器,调用如下:
glEnable(GL_MAP1_VERTEX3);
glEvalCoord1f函数,接受一个参数为曲线的参数值。调用这个函数会通过求值函数求出顶点坐标值,然后内部调用了glVertex。这里使用连线的方式来连接这些顶点:
glBegin(GL_LINE_STRIP);
for(i = 0; I <= 100; i++)
{
glEvalCoord1f((GLfloat)i);
}
glEnd();
计算曲线
OpenGl还提供了更简单的方式来完成上面的任务。我们可以通过glMapGrid函数来设置一个网格,来告诉OpenGL在u的值域的范围内创建一个包含各个点的空间对称的网格。然后,我们调用glEvalMesh,使用指定的图元(GL_LINE或GL_POINTS)来链接各个点。
我们用下面的两个函数调用
glMapGrid1f(100, 0.0f, 100.0f);
glEvalMesh1(GL_LINE, 0, 100);
可以替换下面的代码
glBegin(GL_LINE_STRIP);
for (int i = 0; i <= 100; i++)
{
glEvalCoord1f((GLfloat)i);
}
glEnd();
使用这种方式更为紧凑。
3D表面
创建一个贝塞尔曲面与创建一个贝塞尔曲线类似。除了给出u的定义域之外,还要给出v的定义域。下面的例子是创建一个贝塞尔曲面。与之前不同的是,我们沿着v的定义域定义了3组控制点。为了保持曲面的简单,这几组控制点只是z值不同。用这种方式画的曲面,看起来像是曲线沿z轴的扩展。
//控制点 GLint nNumPoints = 3;
GLfloat ctrlPoints[3][3][3]= {{{ -4.0f, 0.0f, 4.0f},
{ -2.0f, 4.0f, 4.0f},
{ 4.0f, 0.0f, 4.0f }},
{{ -4.0f, 0.0f, 0.0f},
{ -2.0f, 4.0f, 0.0f},
{ 4.0f, 0.0f, 0.0f }},
{{ -4.0f, 0.0f, -4.0f},
{ -2.0f, 4.0f, -4.0f},
{ 4.0f, 0.0f, -4.0f }}}; //画控制点 void DrawPoints(void)
{ int i,j;
glColor3f(1.0f, 0.0f, 0.0f); //把点放大一点,看得更清楚 glPointSize(5.0f);
glBegin(GL_POINTS);
for(i = 0; i < nNumPoints; i++)
for(j = 0; j < 3; j++)
glVertex3fv(ctrlPoints[i][j]);
glEnd();
}
void RenderScene(void)
{
// Clear the window with current clearing color
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// 保存模型视图矩阵
glMatrixMode(GL_MODELVIEW);
glPushMatrix();
//旋转一定的角度方便观察
glRotatef(45.0f, 0.0f, 1.0f, 0.0f);
glRotatef(60.0f, 1.0f, 0.0f, 0.0f);
glColor3f(0.0f, 0.0f, 1.0f); //设置映射方式,只需要设置一次可以在SetupRC中调用。
glMap2f(GL_MAP2_VERTEX_3, //生成的数据类型
0.0f, // u的下界
10.0f, //u的上界
3, //数据中点的间隔
3, //u方向上的阶
0.0f, //v的下界
10.0f, //v的上界
9, // 控制点之间的间隔
3, // v方向上的阶
&ctrlPoints[0][0][0]); //控制点数组
//启用求值器
glEnable(GL_MAP2_VERTEX_3);
//从0到10映射一个包含10个点的网格
glMapGrid2f(10,0.0f,10.0f,10,0.0f,10.0f);
// 计算网格
glEvalMesh2(GL_LINE,0,10,0,10);
//画控制点
DrawPoints();
glPopMatrix();
glutSwapBuffers();
}
在这里我们用glMap2f替换了之前的glMap1f, 这个函数指定了u和v两个域上的点。除了指定u的上界和下界之外,还要指定v的上界和下界。v定义域内点的距离是9,因为这里使用了3维数组,包含了3个u值,每个u值又包含了3个点,3x3=9。然后指定v方向上的阶,即每个u分支上v方向有多少个点。最后一个参数是指向控制点的指针。
然后我们设置求值器.
//启用求值器
glEnable(GL_MAP2_VERTEX_3);
//从0到10映射一个包含10个点的网格
glMapGrid2f(10,0.0f,10.0f,10,0.0f,10.0f);
计算网格网格表面,用线的方式表示。
// 计算网格
glEvalMesh2(GL_LINE,0,10,0,10);
光照和法线
求值器还可以帮我们生成表面的法线,只需简单的修改一些代码:
把glEvalMesh2(GL_LINE, 0, 10, 0, 10);替换为glEvalMesh2(GL_FILL, 0, 10, 0, 10);然后在初始化时 SetupRC中调用glEnable(GL_AUTO_NORMAL);就可以得到一个收到光照的曲面了。
附Java/C/C++/机器学习/算法与数据结构/前端/安卓/Python/程序员必读/书籍书单大全:
(点击右侧 即可打开个人博客内有干货):技术干货小栈
=====>>①【Java大牛带你入门到进阶之路】<<====
=====>>②【算法数据结构+acm大牛带你入门到进阶之路】<<===
=====>>③【数据库大牛带你入门到进阶之路】<<=====
=====>>④【Web前端大牛带你入门到进阶之路】<<====
=====>>⑤【机器学习和python大牛带你入门到进阶之路】<<====
=====>>⑥【架构师大牛带你入门到进阶之路】<<=====
=====>>⑦【C++大牛带你入门到进阶之路】<<====
=====>>⑧【ios大牛带你入门到进阶之路】<<====
=====>>⑨【Web安全大牛带你入门到进阶之路】<<=====
=====>>⑩【Linux和操作系统大牛带你入门到进阶之路】<<=====天下没有不劳而获的果实,望各位年轻的朋友,想学技术的朋友,在决心扎入技术道路的路上披荆斩棘,把书弄懂了,再去敲代码,把原理弄懂了,再去实践,将会带给你的人生,你的工作,你的未来一个美梦。