【机器学习案例一】PM2.5的预测(回归)
基于回归分析的PM2.5预测
- 案例背景
- 数据预处理
- 普通线性回归
- 要求
- 模型参数
- 训练模型
- 训练效果
- 岭回归
- 要求
- 模型参数
- 格子搜索确定最优惩罚因子
- 用最优惩罚因子训练模型
- Lasso回归
- 要求
- 模型参数
- 格子搜索确定最优惩罚因子
- 用最优惩罚因子训练模型
- 基于lasso回归,评价模型变量的重要性
- XGBRegressor
案例背景
数据集 pm2.5 中给出了与预测 pm2.5 有关的气象数据。请利用 2010年至 2013 年的数据作为训练集对 2014 年的 pm2.5 数据进行预测。考虑使用的预测变量包括:hour(日内小时)、dewp(露点)、temp(气温)、pres(气压)cbwd(风向)、lws(风速)、ls(累积降雪)、lr(累积降雨),其中 hour 与 cbwd 应当作类别变量处理。
数据预处理
- 导入库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
import warnings
# filter warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
from sklearn import linear_model
- 读取数据
df=pd.read_csv('pm25.csv')
- 处理缺失值
- 查看缺失值情况
df.isna().sum()
只有pm25这一列数据有空值,一共2043行。而总的数据集的数据一共43800行,包含空值的数据所占总数据集的比例较少,可以直接删除。
2. 删除缺失值
df.dropna(inplace=True)
- 更改数据类型
df['cbwd']=df['cbwd'].astype(str)
df['hour']=df['hour'].astype(str)
- 数据了解
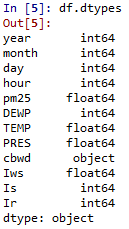
df.columns
[‘year’, ‘month’, ‘day’, ‘hour’, ‘pm25’, ‘DEWP’, ‘TEMP’, ‘PRES’, ‘cbwd’, ‘Iws’, ‘Is’, ‘Ir’]
df.dtypes
- 划分训练集测试集
x=df.loc[:,['hour','DEWP','TEMP','PRES','cbwd','Iws', 'Is', 'Ir']]
y=df.loc[:,['pm25']]
x=pd.get_dummies(x)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.3,random_state = 1)
普通线性回归
要求
请建立普通的线性回归模型,并分别对训练集和测试集的预测精度进行评价。
模型参数
linear_model.LinearRegression().get_params()
{‘copy_X’: True, ‘fit_intercept’: True, ‘n_jobs’: None, ‘normalize’: False}
fit_intercept:是否有截据,如果没有则直线过原点;
normalize:是否将数据归一化(标准化);
copy_X:默认为True,当为True时,X会被copied,否则X将会被覆写;
n_jobs:默认值为1。计算时使用的核数
训练模型
linear=linear_model.LinearRegression()
linear.fit(x_train,y_train)
linear.score(x_train,y_train)
linear.score(x_test,y_test)
回归系数
linear.coef_
linear.intercept_
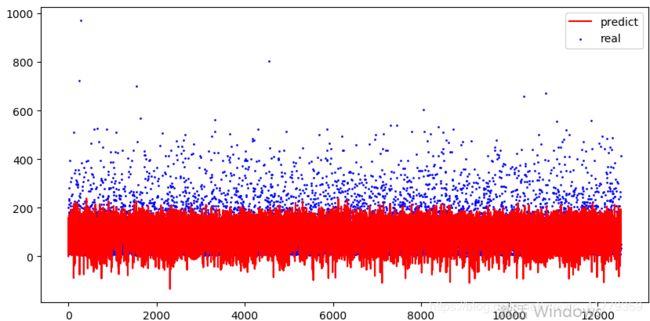
训练集精度:0.295160
测试集精度:0.292433
- 数据标准化
linear=linear_model.LinearRegression(normalize=True)
linear.fit(x_train,y_train)
linear.score(x_train,y_train)
linear.score(x_test,y_test)
训练集精度:0.295146
测试集精度:0.292365
将数据进行标准化处理以后,测试精度和训练精度几乎没有改进
训练效果
- 均方误差
y_hat=linear.predict(x_train)
y_pre=linear.predict(x_test)
fmse=(y_pre-y_test).T.dot(y_pre-y_test)/len(y_test)
mse=(y_hat-y_train).T.dot(y_hat-y_train)/len(y_train)
训练集:mse=6054
测试集:fmse=5801
- 画图
plt.rcParams['savefig.dpi']=300 #像素
plt.rcParams['figure.dpi'] = 100 #分辨率
plt.rcParams['figure.figsize']=(8.0,6.0)
plt.figure()
plt.scatter(list(range(len(y_pre))),y_test,label='real',color='b',s=1)
plt.plot(list(range(len(y_pre))),y_pre,label='predict',color='r')
plt.legend()
plt.show()
岭回归
要求
建立岭回归模型,并利用基于 5 折交叉验证的格子搜索技术确定最优惩罚因子;在最优惩罚因子下,分别评价岭回归在训练集和测试集的预测精度。
模型参数
from sklearn.linear_model import Ridge
Ridge.get_params()
{‘alpha’: 1.0,‘copy_X’: True,‘fit_intercept’: True, ‘max_iter’: None, ‘normalize’: False,‘random_state’: None, ‘solver’: ‘auto’, ‘tol’: 0.001}
格子搜索确定最优惩罚因子
parameters={'alpha':np.arange(0.0001,0.001,0.0001)}
ridge=Ridge()
ridge_cv=GridSearchCV(ridge,param_grid=parameters,cv=5)
ridge_cv.fit(x,y)
print(ridge_cv.best_params_)
print(ridge_cv.best_score_)
best_params_:0.0009
best_score:0.2797
用最优惩罚因子训练模型
ridge=Ridge(alpha = 0.0009)
ridge.fit(x_train,y_train)
ridge.score(x_train,y_train)
ridge.score(x_test,y_test)
训练集精度:0.2951
测试集精度:0.2924
Lasso回归
要求
请建立 Lasso 回归模型,并利用基于 5 折交叉验证的格子搜索技术确定最优惩罚因子;在最优惩罚因子下,分别评价 Lasso 回归在训练集和测试集的预测精度。
模型参数
from sklearn.linear_model import Lasso
lasso=Lasso()
lasso.get_params()
{‘alpha’: 1.0,
‘copy_X’: True,
‘fit_intercept’: True,
‘max_iter’: 1000,
‘normalize’: False,
‘positive’: False,
‘precompute’: False,
‘random_state’: None,
‘selection’: ‘cyclic’,
‘tol’: 0.0001,
‘warm_start’: False}
格子搜索确定最优惩罚因子
lasso=Lasso()
parameters={'alpha':np.arange(1,10,1)}
lasso_cv=GridSearchCV(lasso,param_grid=parameters,cv=5)
lasso_cv.fit(x,y)
print(lasso_cv.best_params_)
print(lasso_cv.best_score_)
best_params_:{‘alpha’: 1}
best_score:0.2457
lasso=Lasso()
parameters={'alpha':np.arange(0.01,0.1,0.01)}
lasso_cv=GridSearchCV(lasso,param_grid=parameters,cv=5)
lasso_cv.fit(x,y)
print(lasso_cv.best_params_)
print(lasso_cv.best_score_)
best_params_:{‘alpha’: 0.02}
best_score:0.2798
用最优惩罚因子训练模型
lasso=Lasso(alpha=0.02)
lasso.fit(x_train,y_train)
lasso.score(x_test,y_test)
lasso.score(x_train,y_train)
训练集精度:0.2951
测试集精度:0.2923
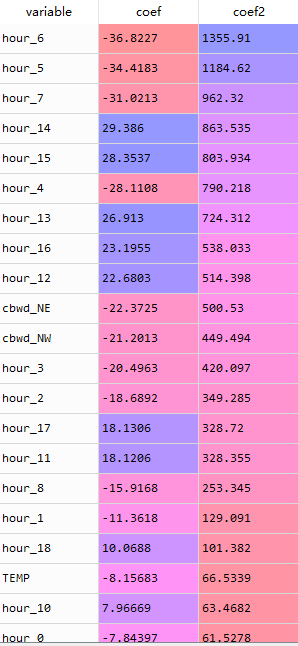
基于lasso回归,评价模型变量的重要性
lasso.coef_
imporant=pd.DataFrame({'variable':x.columns,'coef':lasso.coef_}).sort_values(by='coef',ascending=False)
imporant['coef2']=imporant['coef']**2
imporant=imporant.sort_values(by='coef2',ascending=False)
XGBRegressor
- 模型建立
由于以上模型模型对数据的拟合效果不是很佳,现在尝试用集成学习的模型xgboost对数据进行分析,发现集成学习模型的预测效果明显高于以上模型,但是预测的效果依然不是很理想
from xgboost import XGBRegressor
xgb=XGBRegressor(max_depth=4,n_estimators=301,learning_rate=0.25)
xgb.fit(x_train,y_train)
xgb.score(x_train,y_train)
xgb.score(x_test,y_test)
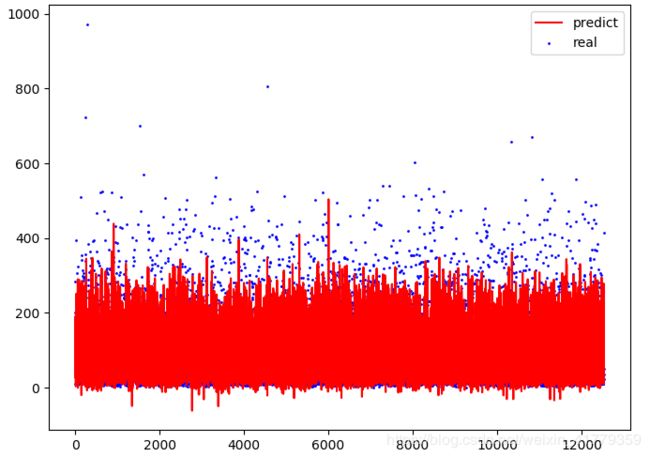
训练集精度:0.5572
测试集精度:0.4525
- 画图
y_pre=xgb.predict(x_test)
plt.rcParams['savefig.dpi']=300
plt.rcParams['figure.dpi'] = 100
plt.rcParams['figure.figsize']=(8.0,6.0)
plt.figure()
plt.scatter(list(range(len(y_pre))),y_test,label='real',color='b',s=1)
plt.plot(list(range(len(y_pre))),y_pre,label='predict',color='r')
plt.legend()
plt.show()