数据结构编程实践(七)创建哈夫曼树、生成哈夫曼编码、完成图片的压缩与解压缩
一、对图片的压缩与解压缩,涉及以下内容:
1.文件读写
2.创建Huffman树
3.生成Huffman编码
4.压缩图片文件
5 . 解压缩图片文件
二、将项目分成三个小任务,下一任务是在上一任务的基础上完成:
1.任务一:统计权值、创建Huffman树
2.任务二:生成Huffman编码、保存压缩文件
3.任务三:解压压缩文件,恢复原文件
下面开始完整的步骤:
三、统计权值、生成Huffman树
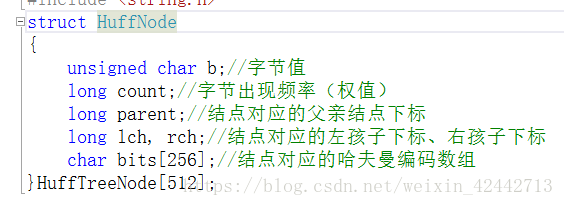
1.Huffman树的存储结构定义
2.统计Huffman树中各结点权值大小的方法及结果
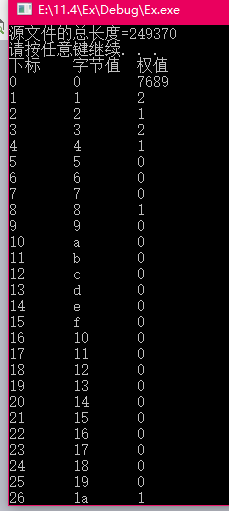
初始化权值为0,通过循环从文件头开始读取文件,直到文件结尾为止,把读到的字节赋值给无符号字符c,然后把与c同值的数组下标所在的元素权值加一。(由于!Feof函数会多读一次文件,所以需要在最后减一得到文件长度。)
程序运行结果如下:
3、 描述生成Huffman树的算法并输出Huffman树各个结点的信息
对树进行初始。由于Huffman树的结点不会超过512,可以采用顺序存储结构,初始数组HuffTreeNode[512]中所有元素包括以下信息:
⦁ b(节点表示的字节):节点表示的字节值,初始可为’\0’。
⦁ count(权值):前面读文件时已统计,此处无需统计。
⦁ parent(父节点):此时哈夫曼树未建立,故设为-1。
⦁ lchild(左孩子):此时哈夫曼树未建立,故设为-1。
⦁ rchild(右孩子):此时哈夫曼树未建立,故设为-1。
⦁ bits数组(结点对应的哈夫曼编码):此时哈夫曼树并未建立,可不设置。
HuffTreeNode[512]数组其中叶子结点在下标小的,所有的叶子结点在前面(0~255),非叶子结点在后面(256~511)。
通过循环,对权值不为0的结点通过强制转型赋与其下标一致的字符值,权值为0的不计。
然后对父节点和孩子赋初始值。图片中可能会出现256种字节,但可能某些字节并未出现,因此判断HuffTreeNode数组前256个元素有权值的元素,让这些元素做为Huffman树的叶子结点,其它的颜色不参于树的生成,提高效率。
采用简单选择排序,将HuffTreeNode数组前256个元素按权值从大到小排序,从而找到有权值的元素个数,记录叶子节点的个数,得到哈夫曼树的总结点数。
每次选HuffTreeNode数组中权值最小的两个元素,其中最小值作为树的左孩子,次小值做为树的右孩子,构建哈夫曼树的后n-1个结点,先预设一个最大权值,通过循环,parent!=-1 说明该结点已在哈夫曼树中,跳出循环重新选择新节点,通过比较找到最小结点和次小结点。然后将该树的根结点作为Huffuman树的非叶子结点。为了保存它们之间的逻辑关系,保存左右孩子的父节点设置,将根节点的权值设置为左右孩子权值之和,将根节点的左右孩子设置。在parent值是0的结点中选取count值最小的两个结点进行合并,规定最小的合并为左孩子,第二小值合并为右孩子,合并生成的根结点的count值为左右孩子权值之和。重复上述过程,直到所有结点合并成一棵树。(parent=0,表示该结点是整棵树的根结点,lch=0和rch=0则表示该结点是叶子结点。)
//生成Huffman树函数
void createTree(HuffNode a[], int n, int m)
{
int i, j;
long min1, pt1;
for (i = n; i < m; i++)//构建哈夫曼树的后n-1个结点
{
min1 = 0x7FFFFFFF;//预设的最大权值,即结点出现的最大次数
for (j = 0; j < i; j++)
{
//parent!=-1 说明该结点已在哈夫曼树中,跳出循环重新选择新节点
if (HuffTreeNode[j].parent != -1)
continue;
if (min1>HuffTreeNode[j].count)
{
pt1 = j;//min最小时的下标
min1 = HuffTreeNode[j].count;//min1为最小
continue;
}
}
//上面已经取出最小的,把它作为哈夫曼树的左结点,设置好相关信息
HuffTreeNode[i].count = HuffTreeNode[pt1].count;
HuffTreeNode[pt1].parent = i;//找到第i个结点的左孩子
HuffTreeNode[i].lch = pt1;//计算左分支权值大小
min1 = 0x7FFFFFFF;
for (j = 0; j < i; j++)
{
if (HuffTreeNode[j].parent != -1)
continue;
if (min1>HuffTreeNode[j].count)
{
pt1 = j;//min最小时的下标
min1 = HuffTreeNode[j].count;//min1为最小
continue;
}
}
HuffTreeNode[i].count += HuffTreeNode[pt1].count;
HuffTreeNode[i].rch = pt1;//设置第i个结点的右孩子
HuffTreeNode[pt1].parent = i;//设置第i个结点右孩子的父结点信息
}
}程序运行结果如下:
需要注意的问题是:
问题一:没有设置最大权值,导致循环比较寻找最小结点时出错。
解决方法:设置最大权值。
问题二:循环构建后n-1个结点时,循环多了一次。
解决方法:修改推出循环条件。
四、生成Huffman编码
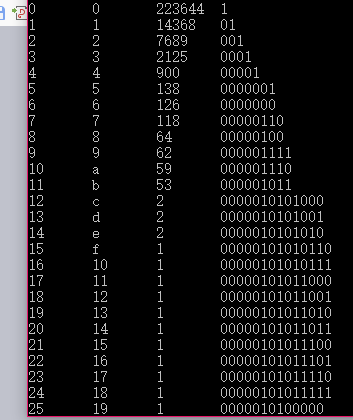
1、 描述如何生成Huffman编码,并输出相应叶子结点对应的Huffman编码
哈夫曼树从根到每个叶子都有一条路径,对路径上的各分支约定指向左子树分支编码为0,右子树分支编码为1,从根到每个叶子相应路径上的0和1组成的序列就是这个叶子节点的编码。从叶子结点出发去判断分支编码为0或为1,当到达根结点时编码结束。初始时字符数组bits只有一个结束符。可通过for循环依次对n个叶子结点编码,在for循环里面先对AscII码为0的字符,编码数组即为\0结束符,置左分支编码0,置右分支编码1,拷贝,留出位置放当前的编码,通过拷贝把\0复制,memmove不出现重叠部分被覆盖,再依次存储连接"0" "1"编码。
//编哈夫曼码
int f;
for (i = 0; i < n; i++)//为每一个叶子结点编码
{
f = i;
HuffTreeNode[i].bits[0] = 0;//AscII码为0的字符,即为\0结束符
while (HuffTreeNode[f].parent != -1)//若没找到根节点
{
j = f;//也就是i
f = HuffTreeNode[f].parent;
if (HuffTreeNode[f].lch == j)//置左分支编码0
{
j = strlen(HuffTreeNode[i].bits);
//拷贝,留出位置放当前的编码
//j+1意味拷贝时把\0复制,memmove不出现重叠部分被覆盖
memmove(HuffTreeNode[i].bits + 1, HuffTreeNode[i].bits, j + 1);
//依次存储连接"0" "1"编码
HuffTreeNode[i].bits[0] = '0';//左分支记为0
}
else//置右分支编码1
{
j = strlen(HuffTreeNode[i].bits);
//拷贝,留出位置放当前的编码
//j+1意味拷贝时把\0复制,memmove不出现重叠部分被覆盖
memmove(HuffTreeNode[i].bits + 1, HuffTreeNode[i].bits, j + 1);
//依次存储连接"0" "1"编码
HuffTreeNode[i].bits[0] = '1';//右分支记为0
}
}
}
for (int i = 0; i < 257; i++)
printf("%d\t%x\t%d\t%s\n", i, i, HuffTreeNode[i].count,HuffTreeNode[i].bits);
system("pause");程序运行结果如下:
2、 压缩文件时,写入文件只需要写入Huffman编码吗?如果还需要写入其它信息,包括一些什么信息?
除了编码,还需要写入一下内容。
信息一:原文件长度。
信息二:当前文件的长度。
信息三:叶子结点总数。
信息四:各个结点对应的字节。
信息五:各个结点的编码长度。
信息六:叶子n对于的哈夫曼编码。
需要注意的问题:
问题二:对左右分支编码混淆。
解决方法:左分支记为0,右分支记为1。
五、生成Huffman编码、保存压缩文件
//写入部分内容
ofp = fopen("1", "wb");//打开文件进行写入
if (ofp == NULL)
{
printf("\n\t文件打开失败!\n\n");
system("pause");
}
fseek(ifp, 0, SEEK_SET);//SEEK_SET指文件头,将文件指针指向待压缩文件的开始位置
fwrite(&flength, sizeof(int), 1, ofp);//在压缩文件头写入文件的总长度,占2个字节
fseek(ofp, 8, SEEK_SET);//重定位压缩文件指针,从头偏移8个字节,留出空间写其他信息,并写入哈夫曼编码准备
//编码源文件
char buf[512];//定义缓冲区,保存字节的huffman编码
buf[0] = 0;//初始为'\0'
long newf = 0;//统计字符个数,可判断源文件是否读完
int pt1 = 8;//统计文件的长度,哈夫曼编码从第8个字节开始写入
while (!feof(ifp))//扫描源文件
{
//从文件中读取一个字符,读取一个字节后,光标位置后移一个字节。
c = fgetc(ifp);
f++;
for (i = 0; i < n; i++)
{
//找到取出字符对应哈夫曼树中叶子结点,并得到相应的下标去找相应的编码
if (c == HuffTreeNode[i].b)
break;
}
strcat(buf, HuffTreeNode[i].bits);//找到当前字符的哈夫曼编码,连接到buf中
//若长度大于8,进行拆分写入,若小于8,则继续取下一个字符的哈夫曼码凑一个字节,凑满写入
j = strlen(buf);//统计该字符编码的长度
c = 0;
while (j >= 8)//若当前编码的长度大于等于8,则要进行拆分,分两个字节存
{
for (i = 0; i < 8; i++)
{
if (buf[i] == '1')
c = (c << 1) | 1;
else
c = c << 1;
}
///
fwrite(&c, 1, 1, ofp);
pt1++;
strcpy(buf, buf + 8);//把buf后一个字节起的所有内容复制到buf中,即一个字节取
j = strlen(buf);
}
if (f == flength)//若源文件所有的字符取完,结束
break;
}
if (j > 0)
{
strcat(buf, "00000000");
for (i = 0; i < 8; i++)
{
if (buf[i] == '1')
c = (c << 1) | 1;
else
c = c << 1;
}
fwrite(&c, 1, 1, ofp);//把最后一个字节写入文件中
pt1++;
}
//写入剩余文件信息
fseek(ofp, 4, SEEK_SET);//移动文件指针位置到第4个字节
fwrite(&pt1, sizeof(long), 1, ofp);//写入统计压缩后文件的长度,4个字节
fseek(ofp, pt1, SEEK_SET);//移动文件指针到压缩后文件尾
fwrite(&n, sizeof(long), 1, ofp);//写入节点数目,即总的不同字节的个数
for (i = 0; i < n; i++)
{
fwrite(&(HuffTreeNode[i].b), 1, 1, ofp);//写入每个节点的代表的字符
c = strlen(HuffTreeNode[i].bits);
fwrite(&c, 1, 1, ofp);//写入每个字符哈夫曼编码的长度
j = strlen(HuffTreeNode[i].bits);//统计哈夫曼长度
if (j % 8 != 0)//若存储的位数不是8的倍数,则补0
{
for (newf = j % 8; newf < 8; newf++)
strcat(HuffTreeNode[i].bits, "0");//011 00000
}
//将哈夫曼编码字符串变成二进制数
while (HuffTreeNode[i].bits[0] != 0)//这里检查是否到了字符串末尾
{
c = 0;
for (j = 0; j < 8; j++)//字符的有效存储不超过8位,则对有效位数左移实现补0
{
if (HuffTreeNode[i].bits[j] == '1')
c = (c << 1) | 1;
else
c = c << 1;
}
strcpy(HuffTreeNode[i].bits, HuffTreeNode[i].bits + 8);//继续转换后面的字符串
fwrite(&c, 1, 1, ofp);
}
}
long length2 = pt1--;//压缩后的文件大小
double div = ((double)length1 - (double)length2) / (double)length1;//计算文件的压缩率
fclose(ifp);//关闭文件
fclose(ofp);
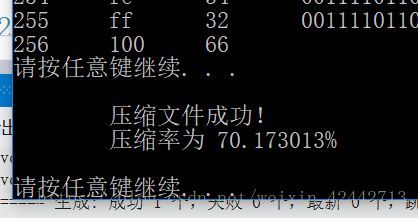
printf("\n\t压缩文件成功!\n");
printf("\t压缩率为 %f%%\n\n", div * 100);
system("pause");1、 将Huffman编码写入压缩文件时,为什么要补0操作?
当若文件读完,buf中的内容可以不足一个字节,需要补0,保证每次写入都是字节的n倍,再对哈夫曼编码位操作,把最后一个字节写入压缩文件。解压缩时可通过记录下来的编码长度无误截断。
2、 将Huffman编码写入压缩文件时,为什么需要移位操作?
为了将编码字符串中的一个个字符转换成数字。
3. 输入压缩的结果不同的文件压缩效率如何?
六、解压压缩文件
1、解压时如何得到原Huffman树及对应的编码?利用itoa函数为什么要补0操作?
通过循环构造Huffman树的n个叶子结点,每读取一个字节,得到huffman树的一个节点,字符对应的哈夫曼编码长度后,再从中每次取出一个字节,转换为二进制表示的字符串。Itoa函数会把一字节转换后的字符串第一个1前面的0去掉,所以要补0知道凑够8位。
2、如何保证每次取出的Huffman编码都能换成相应的字符?每次取出的Huffman编码只能转换成一个字节吗?为什么?
先根据编码长度将结点排序,先求出最长的Huffman编码。当取出的字符个数大于等于最长的编码长度,保证可以转换。这里利用排序算法将前n个结点排序,编码短的在前面,最长的编码在HuffTreeNode数组下标为n-1的位置。定位文件指针,读取压缩文件中原文件的对应的Huffman编码信息。每次读取一字节转成8个“01”字符后暂存在字符数组bx中,直到bx的长度大于等于huffman编码的最大长度,才将相应的编码转化成相应的字节值。这里读取一字节利用itoa函数转换,如长度不足8位要在前面补足0。
3、输出解压缩的结果
需要注意的问题是:
问题一:定位文件指针出错。
解决方法:调试。
问题二:没有补0
解决方法:利用stract函数对字符串补‘0’。
到此为止,基本实现了创建哈夫曼树、生成哈夫曼编码、完成图片的压缩与解压缩的功能,下面附上完整的代码:
Huffman.h头文件:
#include
#include
#include
#include
struct HuffNode
{
unsigned char b;//字节值
long count;//字节出现频率(权值)
long parent;//结点对应的父亲结点下标
long lch, rch;//结点对应的左孩子下标、右孩子下标
char bits[256];//结点对应的哈夫曼编码数组
}HuffTreeNode[512];
//生成Huffman树函数
void createTree(HuffNode a[], int n, int m);
//压缩文件
void compass();
//解压缩文件
void uncompress(); 主函数:
#include "Huffman.h"
//生成Huffman树函数
void createTree(HuffNode a[], int n, int m)
{
int i, j;
long min1, pt1;
for (i = n; i < m; i++)//构建哈夫曼树的后n-1个结点
{
min1 = 0x7FFFFFFF;//预设的最大权值,即结点出现的最大次数
for (j = 0; j < i; j++)
{
//parent!=-1 说明该结点已在哈夫曼树中,跳出循环重新选择新节点
if (HuffTreeNode[j].parent != -1)
continue;
if (min1>HuffTreeNode[j].count)
{
pt1 = j;//min最小时的下标
min1 = HuffTreeNode[j].count;//min1为最小
continue;
}
}
//上面已经取出最小的,把它作为哈夫曼树的左结点,设置好相关信息
HuffTreeNode[i].count = HuffTreeNode[pt1].count;
HuffTreeNode[pt1].parent = i;//找到第i个结点的左孩子
HuffTreeNode[i].lch = pt1;//计算左分支权值大小
min1 = 0x7FFFFFFF;
for (j = 0; j < i; j++)
{
if (HuffTreeNode[j].parent != -1)
continue;
if (min1>HuffTreeNode[j].count)
{
pt1 = j;//min最小时的下标
min1 = HuffTreeNode[j].count;//min1为最小
continue;
}
}
HuffTreeNode[i].count += HuffTreeNode[pt1].count;
HuffTreeNode[i].rch = pt1;//设置第i个结点的右孩子
HuffTreeNode[pt1].parent = i;//设置第i个结点右孩子的父结点信息
}
}
//压缩文件
void compass()
{
FILE *ifp, *ofp;//ifp指向源文件,ofp指向压缩后的文件
char filename[255];
printf("\t请你输入需要压缩的文件名: ");
gets(filename);//获取文件路径
ifp = fopen(filename, "rb");
if (ifp == NULL)
{
printf("\n\t文件打开失败!\n\n");
system("pause");
return;
}
//////////////////////////////////////////////////////////////////////////////////
unsigned char c;//接收读取的一个字节
int flength = 0;//保存文件的字节数,初始为0
while (!feof(ifp))
{
fread(&c, 1, 1, ifp);//从文件中读取一个字节到c
HuffTreeNode[c].count++;
flength++;//统计源文件长度,每读一字节长度+1
}
flength--;//原文件的长度多计算了一次
int length1 = flength;//源文件的总长度
HuffTreeNode[c].count--;
printf("源文件的总长度=%d\n", length1);
system("pause");
printf("下标\t字节值\t权值\n");
for (int i = 0; i < 257; i++)
printf("%d\t%x\t%d\n", i, i, HuffTreeNode[i].count);
system("pause");
/////////////////////////////////////////////////
for (int i = 0; i < 512; i++)
{
if (HuffTreeNode[i].count != 0)//前面读取文件时已把256种颜色出现的频率计算
{
HuffTreeNode[i].b = (unsigned char)i;//如果有权值,设置叶子结点的字节(符)
}
else
{
HuffTreeNode[i].b = 0;//如果没有权值,表示该字符没有在图片中使用
}
//对结点进行初始化,所有结点的父节点都不存在,左右孩子都不存在
HuffTreeNode[i].parent = -1;
HuffTreeNode[i].lch = HuffTreeNode[i].rch = -1;
}
//////////////////////////////////////////////////////////
HuffNode tmp;
int k, j, q;
for (q = 0; q <= 255; ++q)
{
k = q;
for (j = q + 1; j <= 256; ++j)
if (HuffTreeNode[j].count > HuffTreeNode[k].count)
k = j;
if (k != q)
{
tmp = HuffTreeNode[q];
HuffTreeNode[q] = HuffTreeNode[k];
HuffTreeNode[k] = tmp;
}
}
//将前256个元素根据频率(权值)大小排序
//有序函数中权值为0的结点不参与构造哈夫曼树,因此判断数组中有权值结点的个数,用来构造哈夫曼树
int i, n, m;
for (i = 0; i < 256; i++)
if (HuffTreeNode[i].count == 0)
break;//一旦发现权值为0,后面都为0
n = i;
m = 2 * n - 1;
printf("叶子结点n=%d, 总结点m=%d\n", n, m);
system("pause");
printf("下标\t字节值\t权值\t父亲结点\t左孩子\t右孩子\n");
for (int i = 0; i < 257; i++)
printf("%d\t%x\t%d\t%d\t%d\t%d\n", i,i, HuffTreeNode[i].count, HuffTreeNode[i].parent,HuffTreeNode[i].lch, HuffTreeNode[i].rch);
system("pause");
//////////////////////生成树
createTree(HuffTreeNode, n, m);
printf("生成树\n");
//编哈夫曼码
int f;
for (i = 0; i < n; i++)//为每一个叶子结点编码
{
f = i;
HuffTreeNode[i].bits[0] = 0;//AscII码为0的字符,即为\0结束符
while (HuffTreeNode[f].parent != -1)//若没找到根节点
{
j = f;//也就是i
f = HuffTreeNode[f].parent;
if (HuffTreeNode[f].lch == j)//置左分支编码0
{
j = strlen(HuffTreeNode[i].bits);
//拷贝,留出位置放当前的编码
//j+1意味拷贝时把\0复制,memmove不出现重叠部分被覆盖
memmove(HuffTreeNode[i].bits + 1, HuffTreeNode[i].bits, j + 1);
//依次存储连接"0" "1"编码
HuffTreeNode[i].bits[0] = '0';//左分支记为0
}
else//置右分支编码1
{
j = strlen(HuffTreeNode[i].bits);
//拷贝,留出位置放当前的编码
//j+1意味拷贝时把\0复制,memmove不出现重叠部分被覆盖
memmove(HuffTreeNode[i].bits + 1, HuffTreeNode[i].bits, j + 1);
//依次存储连接"0" "1"编码
HuffTreeNode[i].bits[0] = '1';//右分支记为0
}
}
}
for (int i = 0; i < 257; i++)
printf("%d\t%x\t%d\t%s\n", i, i, HuffTreeNode[i].count,HuffTreeNode[i].bits);
system("pause");
//写入部分内容
ofp = fopen("1", "wb");//打开文件进行写入
if (ofp == NULL)
{
printf("\n\t文件打开失败!\n\n");
system("pause");
}
fseek(ifp, 0, SEEK_SET);//SEEK_SET指文件头,将文件指针指向待压缩文件的开始位置
fwrite(&flength, sizeof(int), 1, ofp);//在压缩文件头写入文件的总长度,占2个字节
fseek(ofp, 8, SEEK_SET);//重定位压缩文件指针,从头偏移8个字节,留出空间写其他信息,并写入哈夫曼编码准备
//编码源文件
char buf[512];//定义缓冲区,保存字节的huffman编码
buf[0] = 0;//初始为'\0'
long newf = 0;//统计字符个数,可判断源文件是否读完
int pt1 = 8;//统计文件的长度,哈夫曼编码从第8个字节开始写入
while (!feof(ifp))//扫描源文件
{
//从文件中读取一个字符,读取一个字节后,光标位置后移一个字节。
c = fgetc(ifp);
f++;
for (i = 0; i < n; i++)
{
//找到取出字符对应哈夫曼树中叶子结点,并得到相应的下标去找相应的编码
if (c == HuffTreeNode[i].b)
break;
}
strcat(buf, HuffTreeNode[i].bits);//找到当前字符的哈夫曼编码,连接到buf中
//若长度大于8,进行拆分写入,若小于8,则继续取下一个字符的哈夫曼码凑一个字节,凑满写入
j = strlen(buf);//统计该字符编码的长度
c = 0;
while (j >= 8)//若当前编码的长度大于等于8,则要进行拆分,分两个字节存
{
for (i = 0; i < 8; i++)
{
if (buf[i] == '1')
c = (c << 1) | 1;
else
c = c << 1;
}
///
fwrite(&c, 1, 1, ofp);
pt1++;
strcpy(buf, buf + 8);//把buf后一个字节起的所有内容复制到buf中,即一个字节取
j = strlen(buf);
}
if (f == flength)//若源文件所有的字符取完,结束
break;
}
if (j > 0)
{
strcat(buf, "00000000");
for (i = 0; i < 8; i++)
{
if (buf[i] == '1')
c = (c << 1) | 1;
else
c = c << 1;
}
fwrite(&c, 1, 1, ofp);//把最后一个字节写入文件中
pt1++;
}
//写入剩余文件信息
fseek(ofp, 4, SEEK_SET);//移动文件指针位置到第4个字节
fwrite(&pt1, sizeof(long), 1, ofp);//写入统计压缩后文件的长度,4个字节
fseek(ofp, pt1, SEEK_SET);//移动文件指针到压缩后文件尾
fwrite(&n, sizeof(long), 1, ofp);//写入节点数目,即总的不同字节的个数
for (i = 0; i < n; i++)
{
fwrite(&(HuffTreeNode[i].b), 1, 1, ofp);//写入每个节点的代表的字符
c = strlen(HuffTreeNode[i].bits);
fwrite(&c, 1, 1, ofp);//写入每个字符哈夫曼编码的长度
j = strlen(HuffTreeNode[i].bits);//统计哈夫曼长度
if (j % 8 != 0)//若存储的位数不是8的倍数,则补0
{
for (newf = j % 8; newf < 8; newf++)
strcat(HuffTreeNode[i].bits, "0");//011 00000
}
//将哈夫曼编码字符串变成二进制数
while (HuffTreeNode[i].bits[0] != 0)//这里检查是否到了字符串末尾
{
c = 0;
for (j = 0; j < 8; j++)//字符的有效存储不超过8位,则对有效位数左移实现补0
{
if (HuffTreeNode[i].bits[j] == '1')
c = (c << 1) | 1;
else
c = c << 1;
}
strcpy(HuffTreeNode[i].bits, HuffTreeNode[i].bits + 8);//继续转换后面的字符串
fwrite(&c, 1, 1, ofp);
}
}
long length2 = pt1--;//压缩后的文件大小
double div = ((double)length1 - (double)length2) / (double)length1;//计算文件的压缩率
fclose(ifp);//关闭文件
fclose(ofp);
printf("\n\t压缩文件成功!\n");
printf("\t压缩率为 %f%%\n\n", div * 100);
system("pause");
}
//解压缩文件
void uncompress()
{
char buf[512];//定义缓冲区,保存字节的huffman编码
buf[0] = 0;//初始为'\0'
char filename[255], outputfile[255], bx[255];
unsigned char c;
long i, j, m, n, f, p, l;
long flength;
FILE *ifp, *ofp;
printf("\t请您输入需要解压缩的文件名: ");
gets(filename);
//以二进制只读方式打开.huf文件,ifp指向该文件
ifp = fopen(filename, "rb");
if (ifp == NULL)
{
printf("\n\t文件打开失败!\n\n");
system("pause");
return;
}
printf("\t将在当前目录下解压,请您输入解压缩后的文件名包括拓展名: ");
gets(outputfile);
//以二进制写方式打开outpufile文件,ofp指向该文件
ofp = fopen(outputfile, "wb");
if (ofp == NULL)
{
printf("\n\t解压缩文件打开失败!\n\n");
system("pause");
return;
}
//读取文件信息
fread(&flength, sizeof(long), 1, ifp);//读取未压缩时源文件长度
fread(&f, sizeof(long), 1, ifp);//读取压缩文件的长度,位于第4个字节处
fseek(ifp, f, SEEK_SET);//将文件指针定位到存储节点总数的位置
fread(&n, sizeof(long), 1, ifp);//读取节点数
//重构Huffman树及Huffman编码
for (i = 0; i < n; i++)//构造Huffman树的n个叶子结点
{
fread(&HuffTreeNode[i].b, 1, 1, ifp);//读取一个字节,得到huffman树的一个节点
fread(&c, 1, 1, ifp);//读取字符对应的哈夫曼编码长度
p = (long)c;
HuffTreeNode[i].count = p;//count由保存结点权值改为保存结点的编码长度
HuffTreeNode[i].bits[0] = 0;//初始编码为'\0'
if (p % 8>0)
m = p / 8 + 1;//字节数
else
m = p / 8;
for (j = 0; j < m; j++)
{
fread(&c, 1, 1, ifp);//每次取出一个字节
f = c;
_itoa(f, buf, 2);//将f转换为二进制表示的字符串
f = strlen(buf);//long变成二进制时,如不足8位,而不足8位则补0
for (l = 8; l > f; l--)
{
strcat(HuffTreeNode[i].bits, "0");//先在哈夫曼树结点编码补0
}
strcat(HuffTreeNode[i].bits, buf);//补足0后连接已转好的01字符串
}
HuffTreeNode[i].bits[p] = 0;//设置结束符
}
HuffNode tmp;
for (i = 0; i < n; i++)//根据哈夫曼编码的长短,对结点进行排序,编码短的在前面
{
for (j = i + 1; j < n; j++)
{
if (strlen(HuffTreeNode[i].bits) > strlen(HuffTreeNode[j].bits))
{
tmp = HuffTreeNode[i];
HuffTreeNode[i] = HuffTreeNode[j];
HuffTreeNode[j] = tmp;
}
}
}
p = strlen(HuffTreeNode[n - 1].bits);//编码的最大长度
fseek(ifp, 8, SEEK_SET);//定位文件指针存放原文件哈夫曼编码的位置
m = 0;
bx[0] = 0;//每次处理的解码的字符串
while (1)//通过哈夫曼编码的长短,依次解码,从原来的位存储还原到字节存储
{
while (strlen(bx) < (unsigned int)p)//bx保存最长编码的01串,有可能是一个字符,也uoukeneng是多个字符
{
fread(&c, 1, 1, ifp);//取一个字符,转换成二进制01
f = c;
_itoa(f, buf, 2);
f = strlen(buf);
for (l = 8; l > f; l--)//在单字节内对相应位置补0
{
strcat(bx, "0");
}
strcat(bx, buf);
}
for (i = 0; i < n; i++)
{
if (memcmp(HuffTreeNode[i].bits, bx, HuffTreeNode[i].count) == 0)//找到编码
break;
}
//比较成功后,需继续往后判断bx对应的其他字符
strcpy(bx, bx + HuffTreeNode[i].count);
c = HuffTreeNode[i].b;//得到匹配后的哈夫曼编码对应的字符
fwrite(&c, 1, 1, ofp);//将得到的字符写入目标文件
m++;
if (m == flength)
break;//flength是原文件长度
}
fclose(ifp);//关闭
fclose(ofp);
printf("\n\t解压缩文件成功!\n");
if (m == flength)//对解压缩后文件和原文件相同性比较进行判断(根据文件大小)
printf("\t解压缩文件与原文件相同!\n\n");
else
printf("\t解压缩文件与原文件不同!\n\n");
return;
}
//主函数
void main()
{
//程序入口
int choice;
while (1)//菜单工具栏
{
printf("\t_________________________________________________________\n");
printf("\n");
printf("\t * 压缩、解压缩 小工具 *\n");
printf("\t_________________________________________________________\n");
printf("\t_________________________________________________________\n");
printf("\t|\t\t\t\t\t\t\t|\n");
printf("\t|1.压缩\t\t\t\t\t\t\t|\n");
printf("\t|2.解压缩\t\t\t\t\t\t|\n");
printf("\t|0.退出\t\t\t\t\t\t\t|\n");
printf("\t|_______________________________________________________|\n");
printf("\n");
printf("\t 说明:(1)采用哈夫曼编码\n");
printf("\t (2)适用于字符型文本文件\n");
printf("\n");
do//对用户输入进行容错处理
{
printf("\n\t请选择相应功能(0-2):");
choice = getchar();
getchar();
printf("%c\n", choice);
if (choice != '0'&&choice != '1'&&choice != '2')
{
printf("\t@_@请检查您输入的数字在0-2之间!\n");
printf("\t请再输入一遍!\n");
}
} while (choice != '0'&&choice != '1'&&choice != '2');
if (choice == '1')
{
compass();
}
else if (choice == '2')
{
uncompress();
}
else
{
printf("\t欢迎您再次使用该工具^-^\n");
exit(0);//退出该工具
}
system("pause");//任意键继续
system("cls");//清屏
}
}