排序算法总结

排序算法总结

冒泡排序

冒泡排序是最基础的排序算法。冒泡排序的本质在于交换，即每次通过交换的方式把当前剩余元素的最大值移动到一端，而当剩余的元素减少为0时，排序结束。（数组的零号单元弃用）
代码如下：

#include
int a[1000010];
int main(void)
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d",&a[i]);
	for(int i=1;i<=n-1;i++){
		for(int j=1;j<=n-1-i+1;j++){
			if(a[j]>a[j+1]){
	    	        int temp=a[j];
	    	        a[j]=a[j+1];
	    	       a[j+1]=temp;
		    }
		}
		for(int i=1;i<=n;i++)
		printf("%d ",a[i]);
		printf("\n");
	}
}

输出结果如下：

5
3 4 1 5 2
第1趟:
3 1 4 2 5
第2趟:
1 3 2 4 5
第3趟:
1 2 3 4 5
第4趟:
1 2 3 4 5

时间复杂度分析
假设有n个数需要排序，第一趟需要$n-1$次交换，第二趟需要$n-2$次交换，以此类推…
最坏时间复杂度为:$(n-1)+(n-2)+...+1=$$\frac{n(n-1)}{2}$$\approx O(n^2)$
算法的优化：
如果序列已经为顺序时，上面的代码外层循环仍然要每趟都进行检查是否满足交换的条件，我们可以设置一个计数器，记录交换的次数，当一趟下来交换的次数为0时，直接跳出循环。那么便可以降低平均时间的复杂度。
稳定性：稳定

#include
int a[1000010];
int main(void)
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d",&a[i]);
	for(int i=1;i<=n-1;i++){
		int count=0;
		for(int j=1;j<=n-1-i+1;j++){
			for(int i=1;i<=n;i++)
			if(a[j]>a[j+1]){
	    	int temp=a[j];
	    	a[j]=a[j+1];
	    	a[j+1]=temp;
	    	count++;
		    }
		}
		printf("第%d趟:\n",i);
		for(int i=1;i<=n;i++)
		printf("%d ",a[i]);
		printf("\n");
		if(count==0)
		break;
	}
}

插入排序

简单插入排序

直接插入排序是指，对序列A的n个元素A[1]_{A[n]，令i从2到n枚举，进行n-1趟操作。假设某一趟时，序列A的前$i-1$个元素A[1]}A[i-1]已经有序，而范围[i,n]还未有序，那么该趟从范围[1,i-1]中寻找某个位置j，使得将A[i]插入位置j后(此时A[j]_{A[i-1]会后移一位至A[j+1]}A[i]) 范围[1,i]有序。

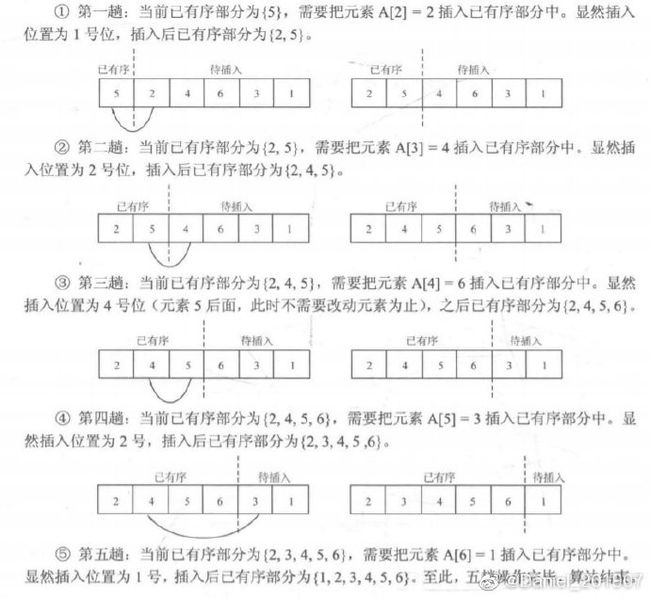
代码如下:

#include
#define maxn 100010
int A[maxn],n; 
int main(void)
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d",&A[i]);
	for(int i=2;i<=n;i++){
		int temp=A[i],j=i;
		while(j>1&&temp

输出结果如下:

5 2 4 6 3 1
第1趟
2 5 4 6 3 1
第2趟
2 4 5 6 3 1
第3趟
2 4 5 6 3 1
第4趟
2 3 4 5 6 1
第5趟
1 2 3 4 5 6

时间复杂度分析:
外层的循环固定会执行$n-1$趟排序。最坏情况下，第一趟关键字比较1次，第二趟2次…最后一趟比较n-1次…
所以最坏情况关键字标记次数：
KCN=1+2+…+(n-1)=$\frac{n(n-1)}{2}$$\approx$O($\frac{n^2}{2}$)
同理最坏情况移动次数：
RMN=1+2+…+(n-1)=$\frac{n(n-1)}{2}$$\approx$O($\frac{n^2}{2}$)
两者相加
最坏时间复杂度为O($n^2$)
平均时间复杂度也为O($n^2$)
稳定性：稳定
算法的优化:
直接插入排序采用顺序查找法查找当前记录的插入位置，这个"查找"我们可以使用二分查找去做，可以加快速度。下面介绍折半插入排序

折半插入排序

折半插入排序和简单插入排序非常类似，区别在于“查找”插入的位置中“查找”使用了“折半查找”来实现。
代码如下：

#include
#include
#define maxn 100010
int A[maxn],n; 
int main(void)
{
   scanf("%d",&n);
   for(int i=1;i<=n;i++)
   scanf("%d",&A[i]);
   for(int i=2;i<=n;i++){
      int temp=A[i],j=i;
      int m,low=1,high=i-1;
      while(low<=high)
      {
      	    m=(low+high)/2;
      	    if(temphigh+1&&j>1)
     {
     	 A[j]=A[j-1];
     	 j--;
     }
     A[j]=temp;
     
      for(int i=1;i<=n;i++)
   	printf("%d ",A[i]);
   	printf("\n");
   }
}

输出结果：

6
5 2 4 6 3 1


2 5 4 6 3 1
2 4 5 6 3 1
2 4 5 6 3 1
2 3 4 5 6 1
1 2 3 4 5 6

我们来理解一下这个算法，while(j>high+1&&j>1)这个语句怎么理解？

---

通过折半查找算法我们知道，首先只能用于有序的数列中，输入待查找的key值，如果key值存在于序列中，则返回key所在的数组下标位置。
那么如果key不不存在与序列中呢，key应该插入到序列的哪一个位置才能保证序列仍然保持有序？
经过分析把key插入到数组下标为（high+1）的位置即可保持序列有序

稳定性：稳定
时间复杂度分析:
在平均情况下，折半插入减少了关键字比较的次数，而记录移动次数不变。因此，折半插入排序的时间复杂度仍然为O($n^2$)

选择排序

选择排序是最简单的排序算法之一，简单选择排序是指，对一个序列A中的元素A[1]~A[n]，令i从1到n枚举，进行n趟操作，每趟从待排序部分[i,n]中选择最小的元素，令其与待排序部分的第一个元素A[i]进行交换，这样元素A[i]就会与当前有序区间[1,i-1]形成新的有序区间[1,i]。于是n趟操作后，所有元素都会是有序的。

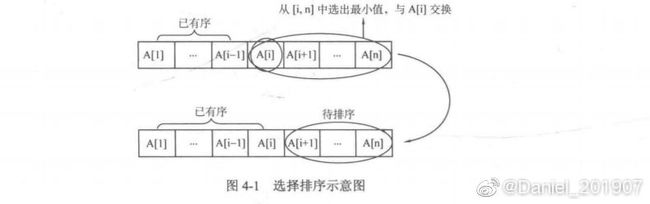
代码如下：

#include
#define maxn 100010
int A[maxn],n; 
int main(void)
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d",&A[i]);
	for(int i=1;i

输出结果：

10
5 4 8 0 9 3 2 6 7 1

0 4 8 5 9 3 2 6 7 1
0 1 8 5 9 3 2 6 7 4
0 1 2 5 9 3 8 6 7 4
0 1 2 3 9 5 8 6 7 4
0 1 2 3 4 5 8 6 7 9
0 1 2 3 4 5 8 6 7 9
0 1 2 3 4 5 6 8 7 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9

更高效的排序算法

二路归并

二路归并是一种基于“归并”思想的排序方法。
原理：将序列两两分组，将序列归并成为[$\frac{n}{2}$]个组，组内单独排序；然后再将这些组两两归并，生成[$\frac{n}{4}$]个组，组内再单独排序，以此类推…
1.序列合并的代码（序列A和B均为递增序列）

void merge(int A[],int L1,int R1,int L2,int R2)
{
	int i=L1,j=L2;
	int temp[maxn],index=0;
	while(i<=R1&&j<=R2){
		if(A[i]<=A[j]){
			temp[index++]=A[i++];
		}
		else{
			temp[index++]=A[j++];
		}
	}
	while(i<=R1) temp[index++]=A[i++];
	while(j<=R2) temp[index++]=A[j++];
	for(i=0;i

2.二路归并(递归算法)的代码

void mergeSort(int A[],int left,int right){
	if(left

3.二路归并(非递归算法)的代码

void mergeSort(int A[]){
	for(int step=2;step/2<=n;step*=2){
		for(int i=1;i<=n;i+=step){
			int mid=i+step/2-1;
			if(mid+1<=n){
				merge(A,i,mid,mid+1,min(i+step-1,n));
			}
		}
	}
}

稳定性：稳定
时间复杂度分析:当有$n$个记录时，需要进行[${\log }_{2}n$]趟归并排序，每一趟归并，其关键字比较次数不超过$n$，元素移动次数都是$n$，因此，归并排序的时间复杂度O($n{\log }_{2}n$)
空间复杂度为：O($n$)
稳定性：稳定
归并排序还可以用于链表结构，代码如下

#include
#include
#define OK 1
struct Node{
   int val;
   Node* next;
};
typedef struct Node* LinkList;
typedef int Status;
LinkList L,p;
Status InitList(LinkList &L)
{
   L=(LinkList)malloc(sizeof(Node));
   L->next=NULL;
   return OK;
}
Status ListCreate(LinkList &L,int n)
{
   LinkList p,r;
   r=L;
   for(int i=0;ival));
   	r->next=p;
   	p->next=NULL;
   	r=p;
   }
   return OK;
}
Status Print(LinkList L)//链表的输出 
{
   LinkList p;
   p=L;
   while(p!=NULL)
   {
   	printf("%d ",p->val);
   	p=p->next;
   }
}
//node -- 链表表头
Node* MergeSort(Node* node){
   //先判断链表长度是否大于1，小于1时无须排序
   if(node!=NULL&&node->next!=NULL){
       //运用快慢指针，找到链表的中间节点
       Node *fast=node->next;
       Node *slow=node;
       while(fast!=NULL&&fast->next!=NULL){
           fast=fast->next->next;
           slow=slow->next;
       }

       //将链表分成两部分进行分割
       Node *p1=MergeSort(slow->next);
   //    Print(p1);
   //   printf("\n");
       slow->next=NULL;                 //这儿很重要，仔细想想为什么
       Node *p2=MergeSort(node);
   //    Print(p2);
   //    printf("\n");

       //对两条子链进行归并
       Node *p0=(Node *)malloc(sizeof(Node));
       Node *p=p0;
       while(p1!=NULL&&p2!=NULL){
           if(p1->valval){
               p->next=p1;
               p1=p1->next;
           }else{
               p->next=p2;
               p2=p2->next;
           }
           p=p->next;
       }

       if(p1!=NULL){
           p->next=p1;
       }

       if(p2!=NULL){
           p->next=p2;
       }

       p=p0->next;
       free(p0);
       return p;
   }
   return node;
}
int main(void)
{
   
   InitList(L);
   int n;
   scanf("%d",&n);
   ListCreate(L,n);
   p=MergeSort(L->next);
   Print(p);
}

输出结果如下：
5
5 4 3 2 1


1 2 3 4 5

快速排序

快速排序是排序算法中平均时间复杂度为O($n{\log }_{2}n$)的一种算法。
基本思想：将A[1]到A[n]，调整序列中元素的位置，使得左侧元素不超过A[1]，右侧所有元素大于A[1]，思想是:two pointers
代码如下

int Partition(int A[],int left,int right){
	int temp=A[left];
	while(lefttemp) right--;
		A[left]=A[right];
		while(left

void QuickSort(int A[],int left,int right)
{
	if(left

加粗的49只是为了作区分
初始状态： 49 38 65 97 76 13 27 49
一趟排序： {27 38 13} 49 {76 97 65 49}
二趟排序： {13} 27 {38} 49 {76 97 65 49}
三趟排序： 13 27 38 49 {49 65} 76 {97}
四趟排序：13 27 38 49 49 {65} 76 97
稳定性：不稳定
快速排序最坏情况退化成O(n^2)，可以让标志位不是A[1]，而是随机产生，那么对任意数据的期望时间复杂度都能达到O($n{\log }_{2}n$)

参考文献：算法导论
算法笔记
数据结构(严蔚敏)