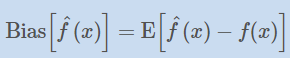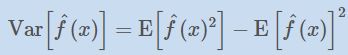机器学习——模型误差分析

机器学习中算法模型的误差分析是一个重要的课题。模型训练完成后，我们通常通过测试集来计算准确率(Accuracy)，来评价模型的优劣。而在模型选择、训练和优化过程中，我们常常用偏差/方差（Bias/Variance），或者欠拟合和过拟合（Underfitting/overfitting）作为优化模型的依据。当我们遇到偏斜类问题(Skewed classes)时，我们又需要新的误差评估量度（Error Metrics）叫做查准率和召回率（Precision/Recall）来权衡（trade off）模型参数的选取。
以下内容是关于偏差/方差（Bias/Variance），和查准率和召回率（Precision/Recall）的整理。

1、偏差/方差（Bias/Variance）

1.1 基本概念

偏差 ：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据，如下图第二行所示。

方差：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散，如下图右列所示。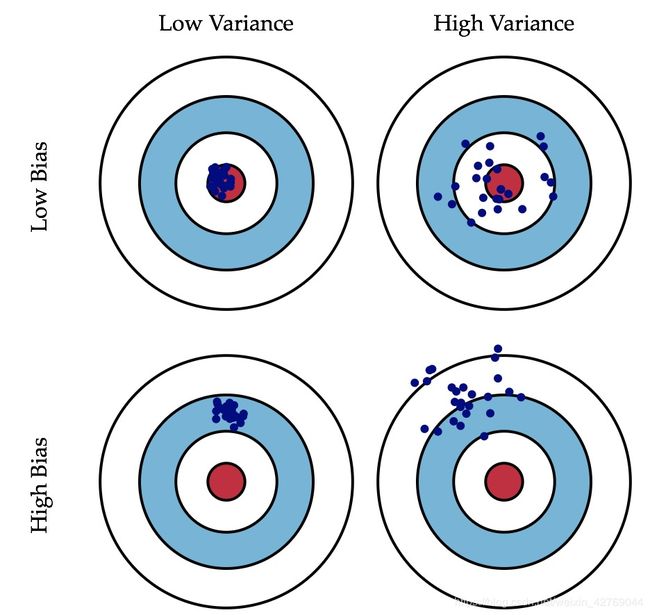
其他表述：（我更喜欢周志华老师的描述）
在忽略噪声的情况下，泛化误差可分解为偏差、方差两部分。
偏差：度量学习算法的期望预测与真实结果的偏离程度，也叫拟合能力。
方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动造成的影响。

1.2 数学描述

首先，在机器学习中，我们建模的目的就是要找到一个函数。一个理想的、完美的函数是应该能够完美的拟合学习任务的，也就是能够建立一个完美的从输入变量（X）到输出变量（Y）的映射的。但现实世界是不可能完美的，当我们获取实际的数据来训练我们的模型的时候，由于数据存在噪声，我们没法得到这个完美的函数。

用数学定义如下： 假如提供的训练数据是y, 完美函数是f(x) 。则y = f(x) + ϵ。其中ϵ是由于噪声等引起的、不可避免的随机误差。机器学习的目的就是要从这些含有噪声的数据中找出（或者说尽可能的靠近）这个f(x) .也就是要基于训练数据y，构建一个f’(x)来近似f(x)。 f’(x)就是我们平常机器学习中学习（构建）的模型。从上面我们知道，这个模型肯定是存在误差的。这个误差显然包括由于噪声等引起的不可避免的误差（也就是，不管你怎么选择算法，怎么调参优化，都会有。这个误差是你的模型误差的下界）。那除了这个不可避免的误差外，还存在其他误差吗？ 回答是肯定的。除了这个不可避免的误差，还存在偏差和方差。而这两项误差，才是我们能控制的。也就是在建模中，我们要优化我们的模型，降低模型的误差，只能从这两项着手。有时候模型误差高，是因为偏差高，有时候又是因为方差高。所以明白偏差和方差的区别就变得非常重要了。

由上面我们知道：
模型误差 = 方差 + 偏差 + 不可避免的随机误差

用数学公式表示就是：

其中，

此外，我们还可以结合欠拟合和过拟合来理解偏差和方差。
欠拟合，对应偏差高。显然，欠拟合就是本身拟合训练数据都不行，也就是训练误差也高。预测的值离真实值的距离就偏高。用模型复杂度来说，就是模型复杂度不够。处理办法一般有：加特征，换更复杂的模型等。
过拟合，对应方差高。也就是训练得到的模型太拟合训练数据了。不同的训练数据训练的模型效果波动很大。泛化能力弱。用模型复杂度来说，就是模型太复杂了。处理办法一般有：增加训练数据，降维，增加正则项等

2 如何判断偏差和方差

这里以线性回归为例，分析模型多项式维度、正则化的参数λ和训练集数量对模型误差的影响。

2.1 模型多项式次数的影响

2.1.1 确定多项式次数

我们知道在选择线性回归模型的多项式次数（ degree of polynomial）时，方法和步骤为：
1）选择不同的多项式次数 d=1,…,10，如下图。
2）在训练集上依次训练不同多项式的参数θ；
3）通过计算各多项式模型在验证集上的损失函数J_cv(θ^(d))，选择损失函数值最小的，确定为模型的多项式维度d；
4）通过测试集来估计损失J_test(θ^(d))；

假设数据集一般被分为三部分：
1）训练集（Training set）： 60%
2）验证集（Cross validation set）： 20%
3）测试集（Test set）： 20%

2.1.2 影响

一般，模型多项式维度增加时，模型在训练集和验证集上的损失关系如下图：

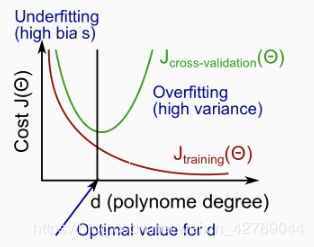
由此，我们可以得到三个结论：
1）高偏差（High bias）： 当多项式次数比较小的时候，此时偏差大，欠拟合，J_train(θ^(d))和J_cv(θ^(d))都比较大，且J_train(θ^(d)) ≈J_cv(θ^(d))；
2）高方差（High variance）： 当多项式次数比较大的时候，此时方差大，过拟合，J_train(θ^(d))越来越小，J_cv(θ^(d))反而变大，且 J_cv(θ^(d))远远大于J_train(θ^(d))；
3）交叉验证集上损失函数 J_cv(θ^(d))取得最小值时，对应的多项式维度d，为最合适的多项式维度。

2.2 正则化参数λ的影响

正则化是防止模型过拟合的一种有效方式，原理在此不再赘述。

2.2.1 正则化参数λ的选择

假设模型多项式的维度已经选定，那么选择正则化参数λ的一般方法和过程如下：
1）选择一套λ参数，如λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24}；
2）计算不同正则化参数下，在训练集上获得的模型参数θ；
3）在验证集上计算交叉验证误差J_cv(θ)，选择误差最小时，对应的正则化参数λ；
4）在测试集上，使用对应维度d，对应模型参数θ，以及选择的正则化参数λ，计算误差J_test(θ)，评价模型。

2.2.2 影响

正则化参数λ不同时，对正则化的线性回归的拟合程度的影响，（假设多项式维度一定，且训练循环次数固定）如下图：

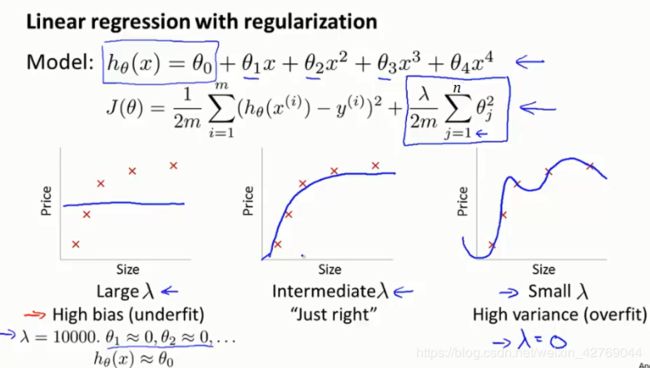
正则化参数λ不同时，对正则化的线性回归，在训练集和验证集上损失函数J_train(θ)和J_cv(θ)影响，如下：

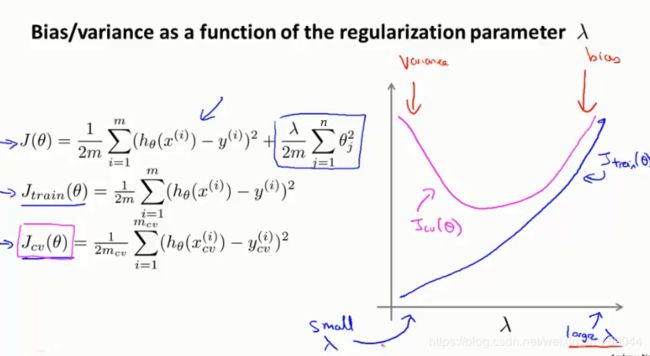
从上面的关系，可以发现：
1）伴随着正则化参数λ的变大，训练集上误差J_train(θ)，越来越大，造成高偏差；
2）无正则化时，验证集上方差较大，随着正则化参数的变大，验证集上误差J_CV(θ)，先变小，再变大，直至高方差，此时，J_train(θ) ≈J_cv(θ)；
3）验证集上误差J_cv(θ)最小时，可以取得合适的正则化参数λ；

2.3 训练集大小的影响

模型训练过程中，随着训练集的增大，一般误差值，即损失函数(均方误差)会逐渐增大，且误差值在训练集大小稳定后趋于稳定。

2.3.1 高偏差（High Bias）的情况

1）小的训练集，J_train(θ) 很小，J_cv(θ)很大；
2）大的训练集，J_train(θ) ≈J_cv(θ)，且都比较大；
3）当学习算法模型已经出现高偏差时，大的训练集对提升算法性能没有帮助。

2.3.1 高方差（High Variance）的情况

1）小的训练集，J_train(θ) 很小，J_cv(θ)很大；
2）大的训练集，随着训练集变大，J_train(θ)误差逐渐增加，J_CV(θ)误差逐渐减小，趋向期望；此时，J_train(θ) < J_cv(θ)；
3）对于存在高方差的算法模型，更大的训练集可以帮助提升算法性能。

2.4 结论

如何发现是否存在过拟合（高方差）或者欠拟合（高偏差）：交叉验证 （cross validation）
高偏差处理方法：(1) 增加特征；（2）boosting方法；
高方差处理方法：（1）降维；（2）增加更多训练数据；（3）增加正则化；（4）bagging方法

3 查准率和召回率（Precision/Recall）

机器学习分类模型存在一种情况叫偏斜类。偏斜类简单理解就是在训练模型时由于正样本和负样本之间的严重不平衡，导致模型最后检测全部都是1或者全部都是0。假设正样本的y值为1，当正样本远远多于负样本的时候，训练好的模型就会一直输出1，这会给我们判断模型优劣带来一定的障碍，比如模型输出1的概率是99.8%，输出0的概率是0.2%，这里我们就会认为模型的精度很好，误差很小。但是其实这种结果是由于数据集的不平衡导致的。因此我们迫切需要一种新方法判断模型的优劣而不仅仅是从accuracy和error，这里就引入了查准率和召回率（Precision/Recall）。
例子：
例如对于癌症的诊断，没患癌症的人肯定远远要多于患有癌症的人。
如果我们设定患有癌症的标签为 1 ，也就是 y = 1；没患癌症的标签为 0 ，也就是 y = 0 。
如果得到 99% 的预测准确率，我们能说这样学习算法是有效的么？
并不一定，因为患有癌症的，很有可能仅仅占据人群的 0.5% ，而一直预测 y = 0 ，也就是预测大家都没有患癌症，就能得到 99.5% 的精准度。
所以通过预测的精准度来判断算法的效果，显然不合理。

3.1 定义

通俗理解：
查准率（Precision）:算法预测的True里面，实际真的True的样本占的比例；
召回率（Recall）:真正的True里面，算法也预测出True的样本占的比例。

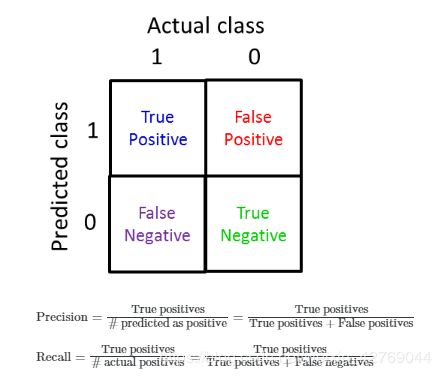
3.2 查准率和召回率的权衡（trade off）

当出现偏斜类，比如垃圾邮件分类，当正样本（垃圾邮件）很少，负样本（正常邮件）很多，模型就会一直识别0，就会导致召回率接近为0。因此当出现偏斜类时就能根据这两个参数判断模型的性能，我们实际应用中希望召回率和查准率两者均高一点，模型性能会好一些。
如果你告诉一个病人说：“你患了癌症”，他们会非常的震惊，因为这是一个非常坏的消息，对人的打击非常大。
所以一般来说，我们希望在非常确信的情况下，才告诉这个人他得了癌症。
对于逻辑回归函数，默认是 h(x) ≥ 0.5，我们就预测 y = 1。而在这样的情况下，我们可以提高这个临界值，设置 h(x) ≥ 0.7，我们才预测 y = 1。
这时候因为我们认为病人有 70% 的几率获得癌症，我们就敢比较确信地告诉他。
这样的情况下，能够相对准确地预测癌症的情况，错误的预测就减少了，那么我们会得到比较高的查准率。
但这样会导致一个问题，因为要保证确信，也就意味着更多真正获得了癌症的人没有被发现，也就是召回率变低了。
这会导致一个病人得了癌症，我们却没有能告诉他获得了癌症，他会因此耽搁治疗而付出生命的代价。
如果我们降低临界值，从 0.5 降低到 0.3 ，就能够提高召回率，不过问题是这样也降低了查准率。
查准率和召回率的关系有可能是这样的：

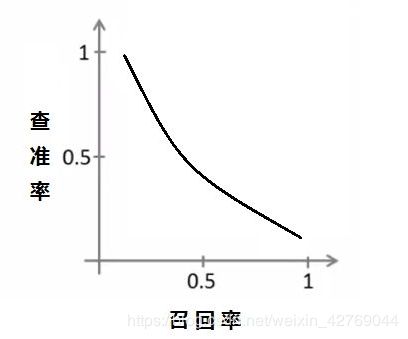
怎么去权衡两者呢？使用 F₁Score 能够更好的衡量算法的效果：

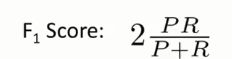
通过和求平均值方法的对比，我们可以看到 F₁Score 能够更好的衡量算法效果，我们召回率和查准率两者均高一点。

参考：

https://ml.berkeley.edu/blog/2017/07/13/tutorial-4/
https://blog.csdn.net/allenalex/article/details/79982644
https://www.zhihu.com/question/20448464
https://blog.csdn.net/syyyy712/article/details/79977020
https://zhuanlan.zhihu.com/p/29922809