3. 强化学习之——无模型的价值函数估计和控制
目录
本次课程主要内容
回顾上次课讲的马尔科夫决策过程
探讨什么是 model-free
Model-free prediction:未知 MDP 情况下的策略估计(值函数估计)
Model-free control:未知 MDP 情况下的值函数优化
本次课程主要内容
model-free prediction:估计一个未知 MDP 模型的 value function
model-free control:优化一个未知 MDP 模型的 value function
回顾上次课讲的马尔科夫决策过程
什么叫MDP已知:Agent 已知奖励函数 R 和状态转移矩阵 P,这也是我们进行策略迭代policy iteration和值迭代value iteration寻找最佳策略的基本要求
策略迭代包含:policy evaluation + policy improvement(在这两个过程中都需要 R 和 P)
值迭代包含:optimal policy + policy extract(这两个过程也都需要 R 和 P)
探讨什么是 model-free
我们之前所做的策略迭代和值迭代其实并没有和环境去交互,已知 MDP 其实就相当于我已知环境的模型了,我知道环境会怎样去变化怎样影响我,所以我完全在脑子里面想就好了啊,相当于 Agent 找到了一个捷径。
但是在真正的实际问题中,我们的 MDP 并不已知或者太大了不能进行计算,这也就要求用 Model-free 的方法去求解。
Model-free 无法获得 R 和 P,但是通过 agent 与环境的交互可以获得一系列的包含每一时刻状态、和它采取的动作和获得的奖励的轨迹:
Agent 要做的就是从这个轨迹中获得的信息,然后改进自己的策略获得更多的奖励
Model-free prediction:未知 MDP 情况下的策略估计(值函数估计)
方法一:蒙特卡罗策略估计(Monte Carlo policy evaluation)
在某种策略下从某些状态开始进行轨迹的采样,最终可以获得很多轨迹,通过对轨迹中的获得的总回报求期望,最终得到的就是这个状态在这种策略下的价值函数
MC 方法不需要 MDP 的 dynamics 和 rewards,也不需要 dynamic programming 的那种 bootstrapping,也不要求状态的马尔科夫性。但是缺点是,由于是采样吗,所以轨迹不能够无限长。
MC 方法的算法流程为:
增量式 MC 方法算法流程:
DP(动态编程)方法 和 MC 方法在策略估计上的区别:
(1)对于 DP 方法来说
(2)对于 MC 方法来说
MC 方法比 DP 方法好在哪里
(1)MC 可以在环境未知的条件下 work,MC 可以是 model-free 的
(2)MC 只更新跟那条轨迹相关的状态,DP 算了两次计算量巨大的加和(所有状态都算一遍),速度慢。而 MC 只是采样,具有很大的计算优势
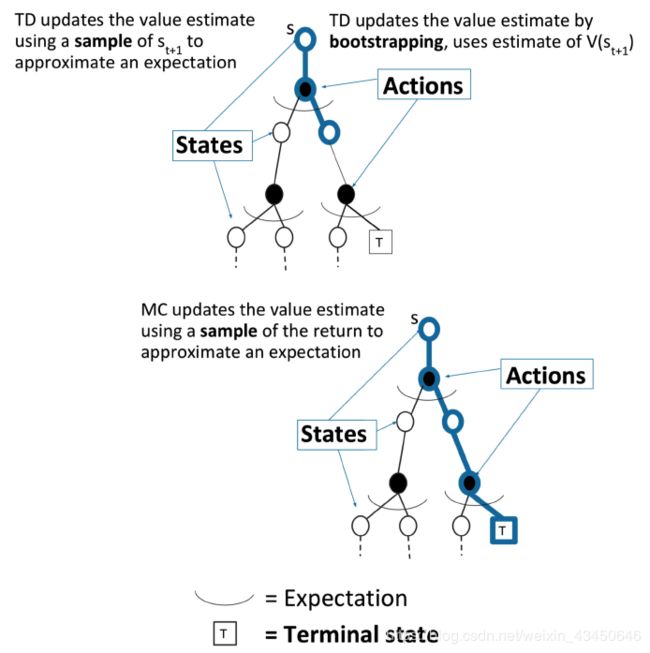
方法二:时域差分学习(Temporal Difference learning)
TD 是一种介于 MC 和 DP 之间的方法:model-free & bootstrapping(对于不完整的episode)
时间差分方法结合了蒙特卡罗 MC 的采样方法(即做试验)和动态规划方法 DP 的bootstrapping(利用后继状态的值函数估计当前值函数)
TD 算法的流程:
TD 方法与 MC 方法的差别:
TD 算法的推广:之前是一步的TD,现在推广为 n-step 的 TD
对于 MC,DP 和 TD 来说,boothstrapping 和 sampliing 的运用
(1)Boothstrapping
MC not
DP yes
TD yes
(2)Sampling
MC yes
DP not
TD yes
一些有意思的可视化:
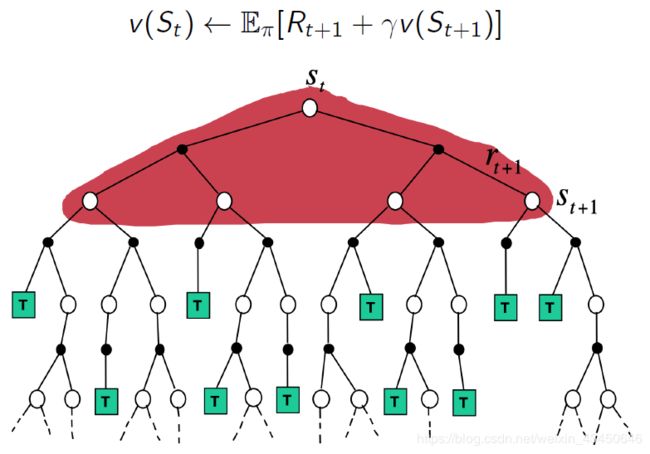
(1)DP 算法的 backup
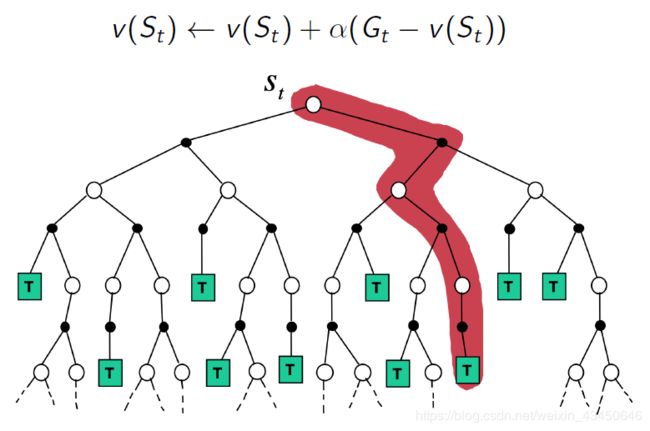
(2)MC 算法的 backup
(3)TD 算法的 backup
(4)TD,MC 和 DP 关系比较转化图
Model-free control:未知 MDP 情况下的值函数优化
首先来复习一下MDP control 中的 policy iteration:初始 π -> 计算 v -> greedy(v) 提升的 π -> 计算 v......这样循环下去
但是,如果我们不知道 R 和 P 的话,我们之前提的 policy iteration 策略迭代优化就无法进行下去:
利用 MC 方法的广义 policy iteration:
因此,这里就有了一种广义的 policy iteration ,用蒙特卡罗 MC 的方法去取代动态编程 DP 的方法去估计 Q 函数,然后用 greedy 方法去改进。也就是利用 MC 方法先把 Q 表的值全部都填上,然后再提升策略。
那么在这个过程中我们要考虑 exploration 和 exploitation 的 tradeoff 的问题【冒进 vs 保守】,这时候就可以引入ε-greedy 的方法 :
当我们 follow 这个 MC ε-greedy 方法进行广义的 policy iteration 时,我们可以证明价值函数是单调递增持续改进的
利用 TD 方法的广义 policy iteration
TD 方法本身相对于 MC 方法具有的优势:方差小、在线的、处理不完整的序列
先来回顾一下 TD prediction
TD prediction 可以预测 V function,那么怎么去把它应用到 Q function 里面呢?—— 有了一种叫On-Policy TD control 的算法叫做 Sarsa【Sarsa 就是 S A R S A 这样进行循环的意思】。至于说什么叫 on-policy 呢,其实就是说这个 policy 既是我们采集数据用的 policy,又是我们优化的对象
Sarsa 的算法流程:
Sarsa 伪算法图:
扩展:n-step Sarsa,自定义多步长 Sarsa
On-Policy 和 Off-Policy 的对比:
On-Policy:目的是学最佳策略,但是在这个过程中只利用我们现在正在学的这个策略,进行轨迹数据的采集和优化都是用这个策略。
Off-Policy:在策略学习过程中,可以保留两个策略,一个是我们要优化的目标策略 target π ,另一个就是我们拿来探索的策略 action μ ,那么这个用来探索的策略就可以更激进,采集数据的策略也是通过 μ 来获得的,采到的数据给 π 去学习。
Off-Policy图示:让大胆激进的策略去跟环境交互,我只用去学它获得的经验就好了呀
Off-Policy Q-learning 算法思想:
更进一步有 behavior policy 和 target policy 的 Q learning:
Q-Learning 的伪算法框架:
对比 Sarsa 和 Q-Learning 的区别:
(1)从 policy 上对比 Sarsa 和 Q-Learning 的区别:Sarsa 是只利用一个策略,而 Q-Learning 有两个策略
(2)从 backup diagram 上对比 Sarsa 和 Q-Learning 的区别
总的来说,Sarsa 更保守,Q-Learning 更激进冒险,在那个 Cliff Walk 中的结果见下图:Sarsa尽量远离,而 Q-Learning在贴着悬崖边在走,Q-Learning 太冒险,掉下去太多了,所以说它的 learning reward 就更低一点,但是最后训练完成会发现 Q-Learning 表现更好更接近实际的最佳策略。
总结对比 DP 和 TD:
一些相关的 Sarsa 和 Q-Learning 的代码实例:
https://github.com/cuhkrlcourse/RLexample/blob/master/modelfree/cliffwalk.py
https://github.com/cuhkrlcourse/RLexample/tree/master/modelfree
注:本文所有内容源自于B站周博磊老师更新完的强化学习纲要课程,听完之后获益很多,本文也是分享我的听课笔记。周老师Bilibili视频个人主页:https://space.bilibili.com/511221970?spm_id_from=333.788.b_765f75706A96e666f.2
感谢周老师 :)