12_python_tree

树的Python实现

树的嵌套列表实现

• 用Python List来实现二叉树数据结构。
• 递归的嵌套列表实现二叉树，由具有3个元素的列表实现：[root, left, right]
  • 第1个元素是根节点的值（是一个数据项）
  • 第2个元素是左子树（是一个列表）
  • 第3个元素是右子树（是一个列表）
• 嵌套列表法的优点：
  • 子树的结构与树相同，是一种递归数据结构
  • 易扩展到多叉树，仅需要增加列表元素即可

myTree = [
    'a', #根节点 myTree[0]
    
    ['b',#左子树 myTree[1]
     ['d',[],[]],
     ['e',[],[]]],
    
    ['c',#右子树 myTree[2]
     ['f',[],[]],
     []]
]

通过定义一系列函数来符注操作嵌套列表:

#创建仅有根节点的二叉树
def BinaryTree(r): 
    return [r,[],[]]

#将新节点插入树中作为其直接的左子节点（如果已有左子节点，则把原左子节点作为新插入节点的左子节点，新插入节点做直接的左子节点）
def insertLeft(root,newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch,[],[]])
    return root

#将新节点插入树中作为其直接的右子节点（如果已有右子节点，则把原右子节点作为新插入节点的右子节点，新插入节点做直接的右子节点）
def insertRight(root,newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root

#获取根节点数据项
def getRootVal(root):
    return root[0]

#更新根节点数据项
def setRootVal(root,newVal):
    root[0] = newVal

#获取左子树
def getLeftChild(root):
    return root[1]

#获取右子树
def getRightChild(root):
    return root[2]

#应用
r = BinaryTree(3)
insertLeft(r, 4)
insertLeft(r, 5)
insertRight(r, 6)
insertRight(r, 7)
l = getLeftChild(r)
print(l)

setRootVal(l, 9)
print(r)

insertLeft(l, 11)
print(r)
print(getRightChild(getRightChild(r)))

[5, [4, [], []], []]
[3, [9, [4, [], []], []], [7, [], [6, [], []]]]
[3, [9, [11, [4, [], []], []], []], [7, [], [6, [], []]]]
[6, [], []]

树的链表实现

• 使用节点链接法实现树
  • 每个节点保存根节点的数据项，以及指向左右子树的链接
  • 通过left和right属性引用其他BinaryTree类实现

class BinaryTree:
    def __init__(self, rootObj):
        self.key = rootObj  #成员key保存根节点数据项
        
        self.leftChild = None #成员leftChid/rightChild则保存指向左/右子树的引用（同样是BinaryTree对象）
        self.rightChild = None
    
    def insertLeft(self, newNode):
        if self.leftChild == None:
            self.leftChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.leftChild = self.leftChild
            self.leftChild = t
    
    def insertRight(self, newNode):
        if self.rightChild == None:
            self.rightChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.rightChild = self.rightChild
            self.rightChild = t
    
    def getRightChild(self):
        return self.rightChild
    
    def getLeftChild(self):
        return self.leftChild
    
    def setRootVal(self, obj):
        self.key = obj
    
    def getRootVal(self):
        return self.key
    
r = BinaryTree('a')
r.insertLeft('b')
r.insertRight('c')
r.getRightChild().setRootVal('hello')
r.getLeftChild().insertRight('d')

树的应用：表达式解析

树用于表示语言中的句子，可以分析句子的各种语法成分，对句子的各种成分进行处理

• 程序设计语言的编译：词法、语法检查；从语法树生成目标代码
• 自然语言处理：机器翻译、语义理解

---

将表达式表示为树结构：叶节点保存操作数，内部节点保存操作符

• 表达式树层次决定计算的优先级，越底层的表达式，优先级越高。
• 树中每个子树都表示一个子表达式，将子树替换为子表达式值的节点，即可实现求值。

---

表达式解析：从全括号表达式构建表达式解析树，利用表达式解析树对表达式求值，从表达式解析树恢复原表达式的字符串形式

• 全括号表达式要分解为单词Token列表。
  • 其单词分为括号‘（）’、操作符‘±*/’和操作数‘0-9’这几类。左括号是表达式的开始，右括号则是表达式的结束。
  • 例子（3+（45））：[’(’,‘3’,’+’,’(’,‘4’,’’,‘5’,’)’,’)’
• 创建表达式解析式：从左到右扫描全括号表达式的每个单词，依据规则建立解析树。
  • 当前单词是左括号，则为当前节点添加一个新节点作为其左子节点，当前节点下降为这个新节点；如果当前单词是操作符±*/，将当前节点的值设为此符号，为当前节点添加一个新节点作为其右子节点，当前节点下降为这个新节点；如果当前单词是操作数，将当前节点的值设为此数，当前节点上升到父节点；如果当前节点是右括号，则当前节点上升到父节点。
  • 创建空树，当前节点为根节点
  • 读入’(’，创建了左子节点，当前节点下降
  • 读入’3’，当前节点设置为3，上升到父节点
  • 读入’+’，当前节点设置为+，创建右子节点，当前节点下降
  • 读入’(’，创建左子节点，当前节点下降
  • 读入’4’，当前节点设置为4，上升到父节点
  • 读入’’，当前节点设置为，创建右子节点，当前节点下降
  • 读入’5’，当前节点设置为5，上升到父节点
  • 读入’)’，上升到父节点
  • 读入’)’，再上升到父节点

---

建立表达式解析树思路

• 创建左右子树：insertLeft/Right()
• 当前节点设置值：setRootVal()
• 下降到左右子树：setLeft/RightChild()
• 上升到父节点：用一个栈来记录跟踪父节点
  • 当前节点下降时，将下降前的节点push入栈
  • 当前节点需要上升到父节点时，上升到pop出栈的节点即可

def buildPaeseTree(fpexp):
    
    fplist = fpexp.split()#分割为token列表
    pStack = Stack()
    eTree = BinaryTree('')
    pStack.push(eTree)  #入栈下降
    currentTree = eTree
    
    for i in fplist:
        #表达式开始
        if i == '(': 
            currentTree.insertLeft('')
            pStack.push(currentTree) #入栈下降
            currentTree = currentTree.getLeftChild()
        #操作数   
        elif i not in ['+', '-', '*', '/', ')']: 
            currentTree.setRootVal(int(i))
            parent = pStack.pop() #出栈上升
            currentTree = parent
        #操作符
        elif i in ['+', '-', '*', '/']:
            currentTree.setRootVal(i)
            currentTree.insertRight('')
            pStack.push(currentTree) #入栈下降
            currentTree = currentTree.getRightChild()
        #表达式结束
        elif i == ')':
            currentTree = pStack.pop() #出栈上升
        else:
            raise ValueError
    return eTree

pt = buildPaeseTree("((10 + 5) * 3)")

增强程序可读性operator模块，为我们提供了很多常用操作符的函数。当我们在字典中查找一个操作符时，相应的函数功能会被取回。因为这个取回的变量是一个函数，可以按通常调用的方式来调用它们，如函数名(变量1，变量2)。

• 例如，查找符’+’(2,2)就等价于operator.add(2,2)

import operator
print(operator.add)
print(operator.add(1,2))
op = operator.add 
n = op(1,2)
print(n)

3
3

利用表达式解析树求值思路：

• 由于二叉树是一个递归数据结构，可以用递归算法来处理
• 求值递归函数evaluate()：由前述对子表达式的描述，可从树的底层子树开始，逐步向上层求值，最终得到整个表达式的值
  • 基本结束条件：叶节点是最简单的子树，没有左右子节点，其根节点的数据项即为子表达式树的值
  • 缩小规模：将表达式树分为左子树、右子树，即为缩小规模
  • 调用自身：分别调用evaluate()计算左子树和右子树的值，然后将左右子树的值依根节点的操作符进行计算，从而得到表达式的值

import operator
def evaluate(parseTree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}  #操作符字典，函数引用和操作符的映射
    
    leftC = parseTree.getLeftChild()  #缩小规模
    rightC = parseTree.getRightChild()
    
    if leftC and rightC:
        fn = opers[parseTree.getRootVal()]
        return fn(evaluate(leftC),evaluate(rightC))  #递归调用
    else:
        return parseTree.getRootVal()  #基本结束条件

树的遍历

• 遍历Traversal：对一个数据集中的所有数据项进行访问的操作
• 根据对节点访问次序的不同来区分3种遍历
  • 前序遍历preorder: 根 - 左 - 右
  • 中序遍历inorder: 左 - 根 - 右
  • 后序遍历postorder: 左 - 右 - 根

#前序遍历
def preorder(tree):
    if tree:
        print(tree.getRootVal())
        preorder(tree.getLeftChild())
        preorder(tree.getRightChild())
#中序遍历
def inorder(tree):
    if tree != None:
        inorder(tree.getLeftChild())
        print(tree.getRootVal())
        inorder(tree.getRightChild())
#后序遍历
def postorder(tree):
    if tree != None:
        postorder(tree.getLeftChild())
        postorder(tree.getRightChild())
        print(tree.getRootVal())

• 使三种遍历方法成为二叉树类BinaryTree中的内置方法
  • 内置的方法在递归调用方法之前必须检查左右子节点是否存在。
• 但是一般来说，在使用遍历方法，外置函数更好一些。因为很少需要单纯遍历整个树。多数情况下，只是想利用基本的遍历方法来实现其他的事情。

class BinaryTree:
    def preorder(self):
        print(self.key)
        if self.leftChild:
            self.leftChild.preorder()
        if self.rightChild:
            self.rightChild.preorder()
    def inorder(self):
        if self.leftChild:
            self.leftChild.inorder()
        print(self.key)
        if self.rightChild:
            self.rightChild.inorder()
    def postorder(self):
        if self.leftChild:
            self.leftChild.postorder()
        if self.rightChild:
            self.rightChild.postorder()
        print(self.key)

• 后序遍历的一种一般应用：解析树求值

def postordereval(tree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}
    res1 = None
    res2 = None
    
    if tree:
        res1 = postordereval(tree.getLeftChild())  #左子树
        res2 = postordereval(tree.getRightChild()) #右子树
        if res1 and res2:                       #根节点
            return opers[tree.getRootVal()](res1, res2)
        else:
            return tree.getRootVal()

• 生成全括号中缀表达式思路
  • 采用中序遍历递归算法来生成全括号中缀表达式

def printexp(tree):
    sVal = ""
    if tree:
        sVal = '(' + printexp(tree.getLeftChild())
        sVal = sVal + str(tree.getRootVal())
        sVal = sVal + printexp(tree.getRightChild()) + ')'
    return sVal

二叉堆的Python实现

代码实现

• 二叉堆初始化：采用一个列表来保存堆数据，其中表首下标为0的项无用，但为了后面代码可以用到简单的整数整除法，仍保留它。
  • 完美二叉树节点关系：节点p的左子节点为2p，右子节点为2p+1，父节点为p//2。成立前提是：元素索引从1开始，不然会发生偏移

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0

• insert(key)方法：为了保持‘完全二叉树’的性质，新key应该添加到列表末尾
  • 问题：新key添加在列表末尾，无法保持堆次序。虽然对其他路径的次序没有影响，但对于其到根的路径可能破坏次序
  • 解决：将新key沿着路径来上浮到其正确位置。新key的上浮不会影响其他路径节点的堆次序。
• 利用insert(key)方法从无序表生成堆的时间复杂度为：O(nlog n)
  • 对于一个排好序的列表，利用二分搜索找到合适的位置来插入一个key，操作复杂度是O(log n).来源于树的高度
  • 然后插入一个数据项到列表中间需要将列表其他数据项移动为新节点腾出位置，操作复杂度为O(n)

def insert(self, k):
    self.heapList.append(k)  #新key添加到列表末尾
    self.currentSize = self.currentSize + 1
    self.percUp(self.currentSize)  #新key上浮

def percUp(self, i):
    while i // 2 > 0:
        if self.heapList[i] < self.heapList[i//2]:
            self.heapList[i],self.heapList[i//2] = self.heapList[i//2],self.heapList[i]   #与父节点进行交换
        i = i // 2

• delMin()方法：移走整个堆中最小的key，即根节点heapList[1]。为了保持‘完全二叉树’的性质，用最后一个节点来代替根节点
  • 问题：破坏了堆次序
  • 解决：将新的根节点沿着一条路径下沉，直到比两个子节点都小
  • 下沉：如果比子节点大，选择较小的子节点所在路径下沉

def delMin(self):
    retval = self.heapList[1] #移走堆顶
    self.heapList[1] = self.heapList[self.currentSize]
    self.currentSize = self.currentSize - 1
    self.heapList.pop()
    self.percDown(1) #新项下沉
    return retval

def percDown(self, i):
    while (i * 2) <= self.currentSize:
        mc = self.minChild(i)
        if self.heapList[i] > self.heapList[mc]:
            self.heapList[i],self.heapList[mc] = self.heapList[mc],self.heapList[i]  #交换下沉
        i = mc  #沿着路径向下 

def minChild(self, i):
    if (i * 2 + 1) > self.currentSize: #唯一子节点
        return i * 2
    else:
        if self.heapList[i * 2] < self.heapList[i * 2 + 1]:  #左右子节点值比较，返回较小的
            return i * 2
        else:
            return i * 2 + 1

• buildHeap(lst)方法：从无序表生成堆
  • 把无序表看成一个堆，再使用下沉法进行排序，使总代价控制在：O(n)

def buildHeap(self, alist):
    i = len(alist) // 2  #从最后节点的父节点开始，因为叶节点无需下沉
    self.currentSize = len(alist)
    self.heapList = [0] + alist[:]
    print(len(self.heapList),i)
    while i > 0:
        print(self.heapList, i)
        self.percDown(i)
        i = i - 1
    print(self.heapList,i)

代码测试：

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0
    
    def insert(self, k):
        self.heapList.append(k)  #新key添加到列表末尾
        self.currentSize = self.currentSize + 1
        self.percUp(self.currentSize)  #新key上浮

    def percUp(self, i):
        while (i // 2) > 0:
            if self.heapList[i] < self.heapList[i//2]:
                self.heapList[i],self.heapList[i//2] = self.heapList[i//2],self.heapList[i]   #与父节点进行交换
            i = i // 2
        
    def buildHeap(self, alist):
        i = len(alist) // 2  #从最后节点的父节点开始，因为叶节点无需下沉
        self.currentSize = len(alist)
        self.heapList = [0] + alist[:]
        print(len(self.heapList),i)
        while i > 0:
            print(self.heapList, i)
            self.percDown(i)
            i = i - 1
        print(self.heapList,i)
    
    def delMin(self):
        retval = self.heapList[1] #移走堆顶
        self.heapList[1] = self.heapList[self.currentSize]
        self.currentSize = self.currentSize - 1
        self.heapList.pop()
        self.percDown(1) #新项下沉
        return retval

    def percDown(self, i):
        while (i * 2) <= self.currentSize:
            mc = self.minChild(i)
            if self.heapList[i] > self.heapList[mc]:
                self.heapList[i],self.heapList[mc] = self.heapList[mc],self.heapList[i]  #交换下沉
            i = mc  #沿着路径向下 

    def minChild(self, i):
        if (i * 2 + 1) > self.currentSize: #唯一子节点
            return i * 2
        else:
            if self.heapList[i * 2] < self.heapList[i * 2 + 1]:  #左右子节点值比较，返回较小的
                return i * 2
            else:
                return i * 2 + 1
    
alist = [3,1,4,9,6,7,5,8,2,10]
h = BinHeap()
h.buildHeap(alist)
h.insert(2)
print('-------------------------------------')
print(h.heapList)
print(h.delMin())
print(h.heapList)

11 5
[0, 3, 1, 4, 9, 6, 7, 5, 8, 2, 10] 5
[0, 3, 1, 4, 9, 6, 7, 5, 8, 2, 10] 4
[0, 3, 1, 4, 2, 6, 7, 5, 8, 9, 10] 3
[0, 3, 1, 4, 2, 6, 7, 5, 8, 9, 10] 2
[0, 3, 1, 4, 2, 6, 7, 5, 8, 9, 10] 1
[0, 1, 2, 4, 3, 6, 7, 5, 8, 9, 10] 0
-------------------------------------
[0, 1, 2, 4, 3, 2, 7, 5, 8, 9, 10, 6]
1
[0, 2, 2, 4, 3, 6, 7, 5, 8, 9, 10]

堆排序

• 堆排序：指利用堆所设计的一种排序算法。堆是一个近似完全二叉树的结构，并满足堆积的性质：子结点的键值或索引总是小于（或者大于）它的父节点
  • 构造初始堆，将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。
  • 将堆顶元素与末尾元素交换，将最大元素"下沉"到数组末端。
  • 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整加交换步骤，直到整个序列有序。
• 堆排序是一种选择排序，整体主要由构建初始堆加交换堆顶元素和末尾元素并重建堆两部分组成。
  • 构建初始堆经推导复杂度为O(n)
  • 在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)…1]逐步递减，近似为nlogn。
    • 完全二叉树的定义，它的深度至少是log(n+1)
  • 堆排序的最好/最坏/平均时间复杂度一般认为是：O(nlogn)
• 堆排序是不稳定排序。
  • 它在交换数据的时候，是比较父结点和子节点之间的数据，所以，即便是存在两个数值相等的兄弟节点，它们的相对顺序在排序也可能发生变化。
  • 算法稳定性:假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

---

• 在第一个元素的索引为 0 的情形中：
  • 性质一：索引为i的左孩子的索引是: 2i+1，右子节点的索引是:2i+2
  • 性质二：索引为i的父结点的索引是: floor((i-1)/2);
  • 性至三：第一个非叶子节点的索引是:len(alist) // 2 - 1

def big_endian(arr,start,end):    
    root=start    
    child=root*2+1 #左孩子    
    while child<=end:
    #孩子比最后一个节点还大，也就意味着最后一个叶子节点了，就得跳出去一次循环，已经调整完毕     
        if child+1<=end and arr[child]<arr[child+1]:
        #为了始终让其跟子元素的较大值比较，如果右边大就左换右，左边大的话就默认           
            child+=1            
        if arr[root]<arr[child]:
        #父节点小于子节点直接交换位置，同时坐标也得换，这样下次循环可以准确判断：是否为最底层，
        #是不是调整完毕                
            arr[root],arr[child]=arr[child],arr[root]                
            root=child                
            child=root*2+1            
        else:               
            break
def heap_sort(arr): #无序区大根堆排序            
    first=len(arr)//2 - 1    
    for start in range(first,-1,-1):
    #从下到上，从左到右对每个节点进行调整，循环得到非叶子节点        
        big_endian(arr,start,len(arr)-1) #去调整所有的节点    
    for end in range(len(arr)-1,0,-1):        
        arr[0],arr[end]=arr[end],arr[0] #顶部尾部互换位置        
        big_endian(arr,0,end-1) #重新调整子节点的顺序，从顶开始调整    
    return arr
     
def main():    
    l=[3,1,4,9,6,7,5,8,2,10]    
    print(heap_sort(l))

if __name__ == "__main__":  
    main()

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

二叉搜索树的Python实现

定义及操作

• BST搜索树：左子树中键值key都小于都节点，而右子树中键值都大于父节点
  • 首先插入的键成为树的根节点
  • 根据插入顺序不同，生成的BST也不同
• 二叉搜索树的实现：节点和链接结构
  • 需要用到BinarySearchTree和TreeNode两个类，BinarySearchTree的root成员引用根节点TreeNode
  • TreeNode类提供辅助函数：根据节点的位置辨别该节点属于何类子节点（左或右），以及该节点的子节点属于何类子节点（左或右）。还提供辅助函数明确地为每个节点追踪对父节点的引用。

class BinarySearchTree:
    def __init__(self):
        self.root = None
        self.size = 0
    
    def length(self):
        return self.size
    
    def __len__(self): #可以使用python的内置方法求长度了
        return self.size
    
    def __iter__(self):  #迭代
        return self.root.__iter__()

class TreeNode:
    def __init__(self, key, val, left = None, right = None, parent = None):#可选参数的使用
        self.key = key   #键
        self.payload = val  #值
        self.leftChild = left  #左子节点
        self.rightChild = right #右子节点
        self.parent = parent  #父节点
    
    def hasLeftChild(self):
        return self.leftChild
    
    def hasRightChild(self):
        return self.rightChild
    
    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self
    
    def isRightChild(self):
        return self.parent and self.parent.rightChild == self
    
    def isRoot(self):
        return not self.parent
    
    def isLeaf(self):
        return not (self.rightChild or self.leftChild)
    
    def hasAnyChildren(self):
        return self.rightChild or self.leftChild
    
    def hasBothChildren(self):
        return self.rightChild and seld.leftChild
    
    def replaceNodeData(self, key, value, lc, rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self

代码实现

• BinarySearchTree.put(key,val)方法：插入key构造BST
  • 首先看BST是否为空，如果一个节点都没有，那么key成为根节点root；否则，调用一个递归函数_put(key, val, root)来放置key
• BinarySearchTree._put(key, val, currentNode)：辅助方法
  • 如果key比currentNode小，那么_put到左子树。但如果没有左子树，那么key就成为左子节点
  • 如果key比currentNode大，那么_put到右子树。但如果没有右子树，那么key就成为右子节点

def put(self, key, val):
    if self.root:
        self._put(key, val, self,root)
    else:
        self.root = TreeNode(key, val)
    self.size = self.size + 1
    
def _put(self, key, val, currentNode):
    if key < currentNode.key:
        if currentNode.hasLeftChild():
            self._put(key, val, currentNode.leftChild)   #递归左子树
        else:
            currentNode.leftChild = TreeNode(key, val, parent = currentNode)
    else:
        if currentNode.hasRightChild():
            self._put(key, val, currentNode.rightChild)  #递归右子树
        else:
            currentNode.rightChild = TreeNode(key, val, parent = currentNode)
    

• 索引赋值–特殊方法 BinarySearchTree.__ setitem __ ()
  • 特殊方法：前后双下划线
  • 可以myZipTree[‘PKU’] = 100871，即重载[]作为操作符
  • 例子：mytree[3] = “red”

def __setitem__(self, k, v):
    self.put(k, v)

• BinarySearchTree.get()方法：在树中找到key所在的节点渠道payload

def get(self, key):
    if self.root:
        res = self._get(key, self.root)  #递归函数
        if res:  #找到节点
            return res.payload
        else:
            return None
    else:
        return None

def _get(self, key, currentNode):  #返回一个TreeNode给get
    if not currentNode:
        return None
    elif currentNode.key == key:
        return currentNode
    elif key < currentNode.key:
        return self._get(key, currentNode.leftChild)
    else:
        return self._get(key, currentNode.rightChild)

• 索引和归属判断–特殊方法
  • BinarySearchTree.__ getitem __ ()：实现val = myZipTree[‘PKU’]，像访问字典一样
  • BinarySearchTree.__ contains__ ()：实现‘PKU’ in myZipTree的归属判断运算符in

def __getitem__(self, key):
    return self.get(key)

def __contains__(self, key):
    if self._get(key, self,root):
        return True
    else:
        return False

• 迭代器：可以用for循环枚举字典中的所有key
  • __ iter__()：用于实现for迭代
  • yield：有额外的步骤来记住函数运行目前的状态，以便下次使用函数时，继续从当前状态执行。
  • 该特殊方法可以直接调用TreeNode中的同名方法
• TreeNode类中的__ iter__迭代器
  • 迭代器函数用来for迭代，实际上是递归函数
  • yield是对每次迭代的返回值
  • 中序遍历的迭代

def __iter__(self):  
    if self:
        if self.hasLeftChild():
            for elem in self.leftChild:
                yield elem
        yield self.key
        if self.hasRightChild():
            for elem in self.rightChild:
                yield elem

• BinarySearchTree.delete()方法：用_get()方法找到要删除的节点，然后调用remove()来删除，找不到则提示错误

def delete(self, key):
    if self.size > 1:
        nodeToRemove = self._get(key, self.root)
        if nodeToRemove:
            self.remove(nodeToRemove)
            self.size = self.size - 1
        else:
            raise KeyError('Error, key not in tree')
    elif self.size == 1 and self.root.key == key:
        self.root = None
        self.size = self.size - 1
    else:
        raise KeyError('Error, key not in tree')

• BinarySearchTree.__ delitem__ ()特殊方法
  • 实现del myZipTree[‘PKU’]这样的语句操作

def __delitem(self, key):
    self.delete(key)

BinarySearchTree.remove()方法：删除节点后，要求仍保持BinarySearchTree的性质，分为以下3种情形：

• 这个节点没有子节点：直接删除，并把指向该节点的引用移动给其父节点
• 这个节点有一个子节点：将这个唯一的子节点上移，替换掉被删节点的位置
  • 有6种情况考虑，由于有一个左/右子树的情况时对称的，仅考虑当前节点右左子树的情况：
  • 1).当前节点是左子节点：更新当前节点的左子节点指向当前节点的父节点引用，将父节点对左子节点的引用更新到当前节点的左子节点
  • 2).当前节点是右子节点：更新当前节点的左子节点指向当前节点的父节点引用，将父节点对右子节点的引用更新到当前节点的左子节点
  • 3).当前节点是根节点：调用根节点的replaceNodeData()方法更换键、有效负荷、左子节点和右子节点。
• 这个节点有两个子节点（最复杂）：找到被删节点的下一个key值节点，即被删节点的右子树中最小的那个，称为‘后继’。用它来替换被删节点。
  • 可以肯定这个后继节点最多只有1个子节点（本身是叶节点，或仅有右子树）

def remove(self,currentNode):
    if currentNode.isLeaf(): #这个节点没有子节点
        if currentNode == currentNode.parent.leftChild:
            currentNode.parent.leftChild = None
        else:
            currentNode.parent.rightChild = None
            
    elif currentNode.hasBothChildren(): #这个节点有两个子节点
        succ = currentNode.findSuccessor()
        succ.spliceOut()
        currentNode.key = succ.key
        currentNode.payload = succ.payload

    else: #这个节点有一个子节点
        if currentNode.hasLeftChild():
            if currentNode.isLeftChild(): #左左：当前节点的左子节点成为当前节点父节点的新的左子节点
                currentNode.leftChild.parent = currentNode.parent
                currentNode.parent.leftChild = currentNode.leftChild
            elif currentNode.isRightChild(): #右左：当前节点的左子节点成为当前节点父节点的新的右子节点
                currentNode.leftChild.parent = currentNode.parent
                currentNode.parent.rightChild = currentNode.leftChild
            else:
                currentNode.replaceNodeData(currentNode.leftChild.key,
                                            currentNode.leftChild.payload,
                                            currentNode.leftChild.leftChild,
                                            currentNode.leftChild.rightChild)
        else:
            if currentNode.isLeftChild(): #左右：当前节点的右子节点成为当前节点父节点的新的左子节点
                currentNode.rightChild.parent = currentNode.parent
                currentNode.parent.leftChild = currentNode.rightChild
            elif currentNode.isRightChild(): #右右：当前节点的右子节点成为当前节点父节点的新的右子节点
                currentNode.rightChild.parent = currentNode.parent
                currentNode.parent.rightChild = currentNode.rightChild
            else:
                currentNode.replaceNodeData(currentNode.rightChild.key,
                                            currentNode.rightChild.payload,
                                            currentNode.rightChild.leftChild,
                                            currentNode.rightChild.rightChild)

• BinarySearchTree.findSuccessor()方法：寻找后继节点
  • 1).如果节点有右子节点：后继是在其右子树中最小的键
  • 2).如果节点没有右子节点：是其父节点的左子节点，那么父节点是其后继
  • 3).如果节点是其父节点的右子节点：而本身无右子节点，则后继是其父节点的后继，不包括这个节点。
• BinarySearchTree.findMin()方法：找到一个子树中的最小值
  • 最小值在任何二叉搜索树中都是子树的左子树

def findSuccessor(self):
    succ = None
    if self.hasRightChild():
        succ = self.rightChild.findMin()
    else:    #目前不会遇到：因为当前要找后继的节点，其右子树肯定存在
        if self.parent:
            if self.isLeftChild():
                succ = self.parent
            else:
                self.parent.rightChild = None
                succ = self.parent.findSuccessor()
                self.parent.rightChild = self
    return succ

def findMin(self):
    current = self
    while current.hasRightChild():
        current = current.leftChild  #到左下角
    return current

• BinarySearchTree.spliceOut()方法：摘出节点

def spliceOut(self):
    if self.isLeaf():  #摘出叶节点
        if self.isLeftChild():
            self.parent.leftChild = None
        else:
            self.parent.rightChild = None
    elif self.hasAnyChildren():
        if self.hasLeftChild():  #目前不会遇到：因为左右子树肯定存在
            if self.isLeftChild():
                self.parent.leftChild = self.leftChild
            else:
                self.parent.rightChild = self.leftChild
            self.leftChild.parent = self.parent
        else:
            if self.isLeftChild():  #摘出带右子节点的节点
                self.parent.leftChild = self.rightChild
            else:
                self.parent.rightChild = self.rightChild
            self.rightChild.parent = self.parent

全部代码：

class TreeNode:
    def __init__(self,key,val,left=None,right=None,parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    def hasLeftChild(self):
        return self.leftChild

    def hasRightChild(self):
        return self.rightChild

    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self

    def isRightChild(self):
        return self.parent and self.parent.rightChild == self

    def isRoot(self):
        return not self.parent

    def isLeaf(self):
        return not (self.rightChild or self.leftChild)

    def hasAnyChildren(self):
        return self.rightChild or self.leftChild

    def hasBothChildren(self):
        return self.rightChild and self.leftChild

    def replaceNodeData(self,key,value,lc,rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self
            
    def __iter__(self):
        if self:
            if self.hasLeftChild():
                for elem in self.leftChiLd:
                    yield elem
            yield self.key
            if self.hasRightChild():
                for elem in self.rightChild:
                    yield elem

class BinarySearchTree:

    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size

    def __iter__(self):
        return self.root.__iter__()

    def put(self,key,val):
        if self.root:
            self._put(key,val,self.root)
        else:
            self.root = TreeNode(key,val)
        self.size = self.size + 1

    def _put(self,key,val,currentNode):
        if key < currentNode.key:
            if currentNode.hasLeftChild():
                   self._put(key,val,currentNode.leftChild)
            else:
                   currentNode.leftChild = TreeNode(key,val,parent=currentNode)
        else:
            if currentNode.hasRightChild():
                   self._put(key,val,currentNode.rightChild)
            else:
                   currentNode.rightChild = TreeNode(key,val,parent=currentNode)

    def __setitem__(self,k,v):
        self.put(k,v)

    def get(self,key):
        if self.root:
            res = self._get(key,self.root)
            if res:
                return res.payload
            else:
                return None
        else:
            return None

    def _get(self,key,currentNode):
        if not currentNode:
            return None
        elif currentNode.key == key:
            return currentNode
        elif key < currentNode.key:
            return self._get(key,currentNode.leftChild)
        else:
            return self._get(key,currentNode.rightChild)

    def __getitem__(self,key):
        return self.get(key)

    def __contains__(self,key):
        if self._get(key,self.root):
            return True
        else:
            return False

    def delete(self,key):
        if self.size > 1:
            nodeToRemove = self._get(key,self.root)
            if nodeToRemove:
                self.remove(nodeToRemove)
                self.size = self.size-1
            else:
                raise KeyError('Error, key not in tree')
        elif self.size == 1 and self.root.key == key:
            self.root = None
            self.size = self.size - 1
        else:
            raise KeyError('Error, key not in tree')

    def __delitem__(self,key):
        self.delete(key)

    def spliceOut(self):
        if self.isLeaf():
            if self.isLeftChild():
                self.parent.leftChild = None
            else:
                self.parent.rightChild = None
        elif self.hasAnyChildren():
            if self.hasLeftChild():
                if self.isLeftChild():
                    self.parent.leftChild = self.leftChild
                else:
                    self.parent.rightChild = self.leftChild
                self.leftChild.parent = self.parent
            else:
                if self.isLeftChild():
                    self.parent.leftChild = self.rightChild
                else:
                    self.parent.rightChild = self.rightChild
                self.rightChild.parent = self.parent

    def findSuccessor(self):
        succ = None
        if self.hasRightChild():
            succ = self.rightChild.findMin()
        else:    #目前不会遇到：因为当前要找后继的节点，其右子树肯定存在
            if self.parent:
                if self.isLeftChild():
                    succ = self.parent
                else:
                    self.parent.rightChild = None
                    succ = self.parent.findSuccessor()
                    self.parent.rightChild = self
        return succ

    def findMin(self):
        current = self
        while current.hasRightChild():
            current = current.leftChild  #到左下角
        return current

    def remove(self,currentNode):
        if currentNode.isLeaf(): #leaf 
            if currentNode == currentNode.parent.leftChild:
                currentNode.parent.leftChild = None
            else:
                currentNode.parent.rightChild = None
        elif currentNode.hasBothChildren(): #interior
            succ = currentNode.findSuccessor()
            succ.spliceOut()
            currentNode.key = succ.key
            currentNode.payload = succ.payload

        else: # this node has one child
            if currentNode.hasLeftChild():
                if currentNode.isLeftChild():
                    currentNode.leftChild.parent = currentNode.parent
                    currentNode.parent.leftChild = currentNode.leftChild
                elif currentNode.isRightChild():
                    currentNode.leftChild.parent = currentNode.parent
                    currentNode.parent.rightChild = currentNode.leftChild
                else:
                    currentNode.replaceNodeData(currentNode.leftChild.key,
                                                currentNode.leftChild.payload,
                                                currentNode.leftChild.leftChild,
                                                currentNode.leftChild.rightChild)
            else:
                if currentNode.isLeftChild():
                    currentNode.rightChild.parent = currentNode.parent
                    currentNode.parent.leftChild = currentNode.rightChild
                elif currentNode.isRightChild():
                    currentNode.rightChild.parent = currentNode.parent
                    currentNode.parent.rightChild = currentNode.rightChild
                else:
                    currentNode.replaceNodeData(currentNode.rightChild.key,
                                                currentNode.rightChild.payload,
                                                currentNode.rightChild.leftChild,
                                                currentNode.rightChild.rightChild)


mytree = BinarySearchTree()
mytree[3]="red"
mytree[4]="blue"
mytree[6]="yellow"
mytree[2]="at"

print(3 in mytree)
print(mytree[6])
del mytree[2]
print(mytree[2])

for key in mytree:
    print(key,mytree[key])

True
yellow
None
3 red
4 blue
6 yellow

算法分析

• BST的高度就是log n（n是节点的个数）。
• 以put方法为例
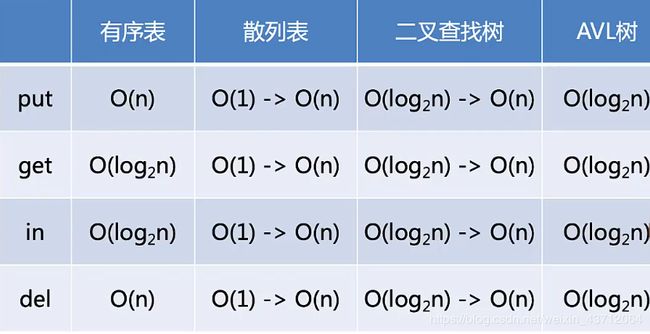
  • 其性能决定因素在于二叉搜索树的高度（最大层次），而其高度又受数据项key插入顺序的影响。（get、in、del方法也是受高度限制的）
  • 如果key的列表是随机分布的话，那么大于和小于根节点key的键值大致相等。而且，这样的树就是平衡树
    • put方法最差性能为：O(log n)
  • key列表极端情况分布（按照从小到大顺序插入时）
    • put方法的极端性能为：O(n)
• 完美平衡二叉树：
  • 在二叉树中，根上有一个节点，下一级有两个，再下一级有四个。当级数为d时，这一级的节点数目为2d。当h代表树的高度时，一个完美平衡二叉树中节点的总数目是：2^(h+1)-1。
  • 一个完美平衡二叉树中左子树和右子树的节点数目是一样多的。

AVL树的Python实现

• 平衡因子：左子树的高度和右子树的高度只差
  • 平衡因子大于0：左重
  • 平衡因子小于0：右重
  • 平衡因子等于0：完美平衡二叉树
• AVL树：树上每个节点的平衡因子是-1，0或1，则这个树是平衡的
  • 叶节点的平衡因子一定是0
• AVL树性能：限制搜索复杂度为：O(log N)，N为节点总数
  • 高度为h的树的节点数:N(h) = 1 + N(h-1) + N(h-2)
  • h = 1.44 * logN(h)

平衡解析

向AVL树插入一个新key，如何保持AVL树的平衡性质？

• 首先，作为BST，新key必定以叶节点形式插入到AVL树种
  • 作为左子节点插入，则父节点的平衡因子会增加1；作为右子节点插入，则父节点的平衡因子会减少1
  • 这种影响可能随着其父节点到根节点的路径已知传递上去，直到传递到根节点为止，或者某个父节点平衡因子被调整到0，不在影响上层节点的平衡因子为止。
  • 无论从-1或者1(非0)调整到0，都不会改变子树高度；高度不变，则不会影响上层平衡因子

def _put(self, key, val, currentNode):
    if key < currentNode.key:
        if currentNode.hasLeftChild():
            self._put(key, val, currentNode.leftChild)
        else:
            currentNode.leftChild = TreeNode(key, val, parent = currentNode)
            self.updateBalance(currentNode.leftChild)   #调整因子
    else:
        if currentNode.hasRightChild():
            self._put(key, val, currentNode.rightChild)
        else:
            currentNode.rightChild = TreeNode(key, val, parent = currentNode)
            self.updateBalance(currentNode.rightChild)  #调整因子
            
def updateBalance(self, node):
    if node.balanceFactor > 1 or node.balanceFactor < -1:
        self.rebalance(node)  #重新平衡
        return
    if node.parent != Node:
        if node.isLeftChild():
            node.parent.balanceFactor += 1
        elif node.isRightChild():
            node.parent.balanceFactor -= 1
            
        if node.parent.balanceFactor != 0:  #调整父节点因子
            self.updateBalance(node.parent)

• rebalance重新平衡：将不平衡的子树进行旋转rotation
  • 视‘左重’或者‘右重’进行不同方向的旋转，同时更新相关父节点引用，更新旋转后被影响节点的平衡因子
  • 例子：右重子树A的左旋转：将A的右子节点B提升为子树的根，将旧根节点A作为新根节点B的左子节点；如果新根节点B原来有左子节点，则将此节点设置为A的右子节点（A的右子节点一定有空）

def rotateLeft(self, rotRoot):
    newRoot = rotRoot.rightChild
    
    rotRoot.rightChild = newRoot.leftChild   
    if newRoot.leftChild != None:
        newRoot.leftChild.parent = rotRoot
        
    newRoot.parent = rotRoot.parent   
    if rotRoot.isRoot():
        self.root = newRoot
    else:
        if rotRoot.isLeftChild():
            rotRoot.parent.leftChild = newRoot
        else:
            rotRoot.parent.rightChild = newRoot
    newRoot.leftChild = rotRoot
    rotRoot.parent = newRoot
    
    #仅有两个节点需要调整因子
    rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor, 0)
    newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor, 0)

def rotateRight(self,rotRoot):
    newRoot = rotRoot.leftChild
    
    rotRoot.leftChild = newRoot.rightChild
    if newRoot.rightChild != None:
        newRoot.rightChild.parent = rotRoot
        
    newRoot.parent = rotRoot.parent
    if rotRoot.isRoot():
        self.root = newRoot
    else:
        if rotRoot.isRightChild():
            rotRoot.parent.rightChild = newRoot
        else:
            rotRoot.parent.leftChild = newRoot
    newRoot.rightChild = rotRoot
    rotRoot.parent = newRoot
    
    rotRoot.balanceFactor = rotRoot.balanceFactor - 1 - max(newRoot.balanceFactor, 0)
    newRoot.balanceFactor = newRoot.balanceFactor - 1 + min(rotRoot.balanceFactor, 0)       

AVL树旋转更复杂的情形:

• 在左旋转之前检查右子节点的因子：如果右子节点左重的话，则右子节点做右旋，然后原节点左旋转
• 在右旋转之前检查左子节点的因子：如果左子节点右重的话，则左子节点做左旋，然后原节点右旋转

def rebalance(self, node):
    if node.balanceFactor < 0: #右重需要左旋
        if node.rightChild.balanceFactor > 0:
            #Do an LR Rotation
            self.rotateRight(node.rightChild) #右子节点左重先右旋
            self.rotateLeft(node)
        else:
            #single left
            self.rotateLeft(node)
    elif node.balanceFactor > 0:  #左重需要右旋
        if node.leftChild.balanceFactor < 0:
            #Do an RL Rotation
            self.rotateLeft(node.leftChild) #左子节点右重先左旋
            self.rotateRight(node)
        else:
            #single right
            self.rotateRight(node)

• AVL树中get方法：时间复杂度仍是O(log n)
  • 因为AVL树始终保持平衡
• AVL树中put方法：时间复杂度仍是O(log n)
  • 需要插入的新节点是叶节点，更新其所有父节点和祖先节点的代价最多为：O(log n)
  • 如果插入的新节点引发了不平衡，重新平衡最多需要2次旋转，但旋转的代价与问题规模无关，是常数：O(1)

代码实现

class AVLTree(BinarySearchTree):
    def _put(self,key,val,currentNode):
        if key < currentNode.key:
            if currentNode.hasLeftChild():
                self._put(key,val,currentNode.leftChild)
            else:
                currentNode.leftChild = TreeNode(key,val,parent=currentNode)
                self.updateBalance(currentNode.leftChild)
        else:
            if currentNode.hasRightChild():
                self._put(key,val,currentNode.rightChild)
            else:
                currentNode.rightChild = TreeNode(key,val,parent=currentNode)
                self.updateBalance(currentNode.rightChild)                

    def updateBalance(self,node):
        if node.balanceFactor > 1 or node.balanceFactor < -1:
            self.rebalance(node)
            return
        if node.parent != None:
            if node.isLeftChild():
                node.parent.balanceFactor += 1
            elif node.isRightChild():
                node.parent.balanceFactor -= 1

            if node.parent.balanceFactor != 0:
                self.updateBalance(node.parent)

    def rebalance(self,node):
        if node.balanceFactor < 0:
            if node.rightChild.balanceFactor > 0:
                # Do an LR Rotation
                self.rotateRight(node.rightChild)
                self.rotateLeft(node)
            else:
                # single left
                self.rotateLeft(node)
        elif node.balanceFactor > 0:
            if node.leftChild.balanceFactor < 0:
                # Do an RL Rotation
                self.rotateLeft(node.leftChild)
                self.rotateRight(node)
            else:
                # single right
                self.rotateRight(node)

    def rotateLeft(self,rotRoot):
        newRoot = rotRoot.rightChild
        rotRoot.rightChild = newRoot.leftChild
        if newRoot.leftChild != None:
            newRoot.leftChild.parent = rotRoot
        newRoot.parent = rotRoot.parent
        if rotRoot.isRoot():
            self.root = newRoot
        else:
            if rotRoot.isLeftChild():
                rotRoot.parent.leftChild = newRoot
            else:
                rotRoot.parent.rightChild = newRoot
        newRoot.leftChild = rotRoot
        rotRoot.parent = newRoot
        rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor, 0)
        newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor, 0)


    def rotateRight(self,rotRoot):
        newRoot = rotRoot.leftChild
        rotRoot.leftChild = newRoot.rightChild
        if newRoot.rightChild != None:
            newRoot.rightChild.parent = rotRoot
        newRoot.parent = rotRoot.parent
        if rotRoot.isRoot():
            self.root = newRoot
        else:
            if rotRoot.isRightChild():
                rotRoot.parent.rightChild = newRoot
            else:
                rotRoot.parent.leftChild = newRoot
        newRoot.rightChild = rotRoot
        rotRoot.parent = newRoot
        rotRoot.balanceFactor = rotRoot.balanceFactor - 1 - max(newRoot.balanceFactor, 0)
        newRoot.balanceFactor = newRoot.balanceFactor - 1 + min(rotRoot.balanceFactor, 0)

总结