网络流详解

network-flows，网络流，传说中的省选算法

先推荐一个讲网络流思路的blog：

https://www.cnblogs.com/ZJUT-jiangnan/p/3632525.html

网络流有两种写法，dinic和sap（isap） 本人太弱了，只会dinic

目的

首先，明确网络流是干什么的

给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).

下面给出一个通俗点的解释

好比你家是汇 自来水厂是源

然后自来水厂和你家之间修了很多条水管子接在一起 水管子规格不一 有的容量大 有的容量小

然后问自来水厂开闸放水 你家收到水的最大流量是多少

如果自来水厂停水了 你家那的流量就是0 当然不是最大的流量
但是你给自来水厂交了100w美金 自来水厂拼命水管里通水 但是你家的流量也就那么多不变了 这时就达到了最大流

理解起来还好吧，也就是上文说的那样

实现

现在知道了到底要求什么了，但是怎么求？

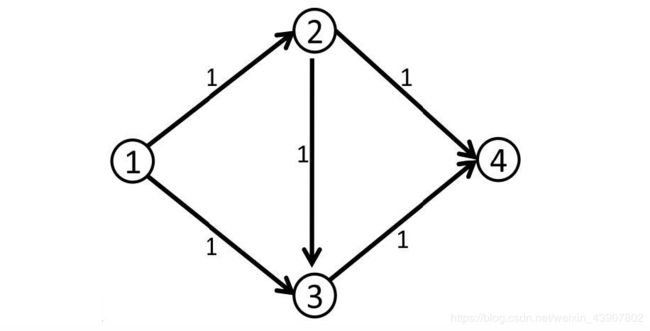
先给个模型如下

首先来手算一下，很容易可以得出这个最大流是走（1，2，4）和（1，3，4）得到的2，即最大流为2

然后对于程序，我们先引入一个叫做残量图的概念

顾名思义，残嘛，就是剩的意思，即剩下的量，我们把一条边的最大容量MAXV和其实际的流量F的差值叫做残量,即

残量=$MAXV-F$

然后我们将残量作为每一条边的权值，构建一个图就叫做残量图，若权值为0，那么就相当于一条断边

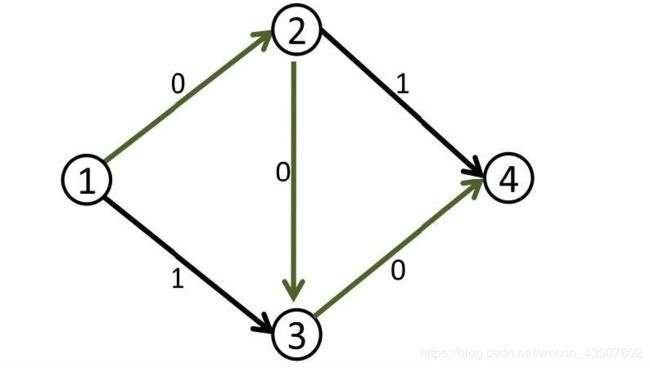
此时，假设我们从源出发进行的某一次dfs到了汇，那么就说明这条路线的流量还可以增加，具体增加的量就被这条路线上的流量最小的那条边决定了，我们把这样的路叫做增广路

就像上图，我们知道（1，2，3，4）这条路线是可以在增大流量的，且最大可增大的流量是1，故我们就将其经过的边的残量-1得到了这个图

然后我们再dfs，却发现不能到达汇了，于是程序这个时候就返回此时的最大流，1

但是并不是这样的啊？？

这个时候我们发现，如果程序在dfs到2的时候若可以向4dfs的话就不会出错了啊！那么这个时候，如果我们给这个图上的每一个点都标上深度的话，我们dfs的时候只允许从低深度往高深度走的话，岂不是可以大幅度避免出错呢？于是这个时候dinic算法的思想就出来了，就是不断用bfs标深度然后不断dfs直到不能到达汇为止

但是仅仅通过标记深度能不能完全解决问题呢？答案是不能的，即使它可以大幅度减少

那如果说我们可以让程序在dfs到3的时候发现问题并后悔不就ok了吗？

如果想要达到这种境界，我们可以写一个人工智能的学习算法，但是注意了，这是竞赛，是来搞笑的不是来毁灭人类的哈哈哈哈

于是有一种最easy的方法就是引入一个反向边的概念（怎么引入这么多概念），即每一条边（u,v）都有一条反向边(v,u),且这两条边的最大容量相等，实际流量之和等于最大流量，即

$MAXV(u,v)=MAXV(v,u)$

$F(u,v)=F(v,u)=MAXV(v,u)=MAXV(u,v)$

由于定义，当一条边的流量+或-a时，其反向边的流量-或+a

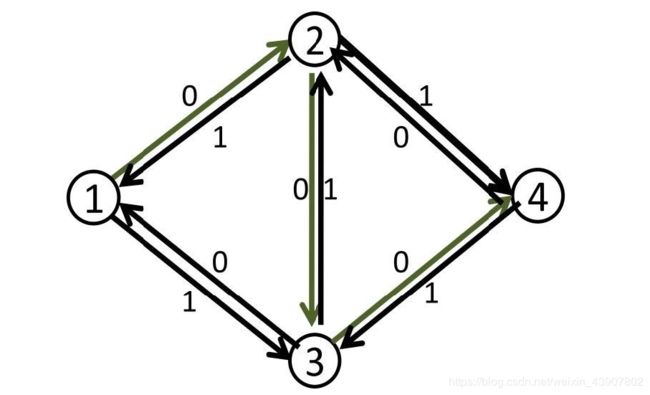
我们若引入反向边的概念后，就有了这样一个图

然后根据dfs，我们找到了增广路（1，2，3，4），然后图就该变成这样

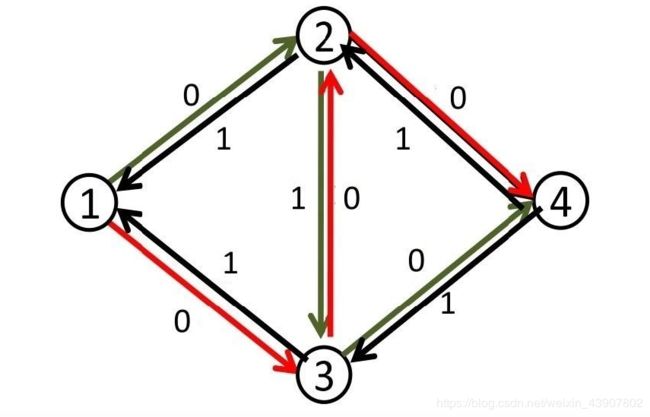
然后我们继续dfs，把反向边也当作可走的边dfs，然后得到了增广路（1，3，2，4）

然后图就成了这样

最大流为2

仔细观察可以发现，上图其实和我们直接dfs（1，2，4）和（1，3，4）得到的结果一样！！这也就正确了！！

但是为什么可以正确呢？程序并没有大叫一声“啊，不该这样走！”

其实奥妙在第2个dfs

当程序将边（3，2）的流量加一，（2，3）的流量减一时，其实就相当于把边（2，3）的流量给退回去了（不信你看退回后的（2，3）和原图的（2，3）是不是一样的），然后还把本来属于路径（1，2，3，4）的流量“交付”给了（1，3），于是就有了两条路（1，2，4）和（1，3，4）

这就是其奥妙所在

于是这个算法框架就此浮出水面：

先标深度再用dfs找一次增广路然后再bfs标深度在dfs然后bfs，dfs，bfs，dfs,bfs,dfs,bfs,dfs…直到bfs时发现断层，说明此时已经找到了最大流

下面给个代码吧，有些细节还需要看看

题目来源：luoguP1343

//dinic
#include
using namespace std;
#define INF INT_MAX
const int maxn=200+5;
const int maxm=2000+5;
int n,m,x,cnt=0;
int head[maxn];
int dis[maxn];
struct node
{
    int e;
    int v;
    int nxt;
}edge[maxm<<1];
//**********************************function
inline int read(){
   int ans=0;char r=getchar();
   while(r<'0'||r>'9')r=getchar();
   while(r>='0'&&r<='9'){ans=ans*10+r-'0';r=getchar();}
   return ans;
}
inline void addl(int u,int v,int w)
{
    edge[cnt].e=v;
    edge[cnt].v=w;
    edge[cnt].nxt=head[u];
    head[u]=cnt++;
}
void datasetting()
{
    memset(head,-1,sizeof(head));
    n=read();m=read();x=read();
    int a,b,c;
    for(int i=0;i<m;i++)
    {
        a=read();b=read();c=read();
        addl(a,b,c);addl(b,a,0);//加边和反向边
    }
}
bool bfs()//bfs找深度
{
    memset(dis,-1,sizeof(dis));//注意！不要忘了这句
    dis[1]=0;//起点深度为0，从源向汇bfs
    queue<int>q;
    q.push(1);
    while(!q.empty())
    {
        int r=q.front();q.pop();
        for(int i=head[r];i!=-1;i=edge[i].nxt)
        {
            int j=edge[i].e;
            if(dis[j]==-1&&edge[i].v)//如果这个点还没有被bfs且这条边的流量不为0
            {
                dis[j]=dis[r]+1;
                q.push(j);
            }
        }
    }
    return dis[n]!=-1;//若不可以到终点（起点）就返回false 
}
int dfs(int u,int flo)//dfs就是求节点u及其子树在残量为flo时的最大增量 
{
    if(u==n)return flo;//如果是汇，直接返回flo
    int detla=flo;//用一个变量来保存flo，以方便更新其剩余残量
    for(int i=head[u];i!=-1;i=edge[i].nxt)
    {
        int v=edge[i].e;
        if(dis[v]==(dis[u]+1)&&(edge[i].v)>0)//如果满足深度条件且边可以走
        {
            int d=dfs(v,min(detla,edge[i].v));//向下递归
            //求v及其后续节点在残量为min(detla,edge[i].v)时的最大流量
            edge[i].v-=d;edge[i ^ 1].v+=d;//边的处理
            //注意，编号为i的边的反向边的编号为i^1,这是根据存边时的cnt决定的
            detla-=d;//将本节点的剩余残量值更新
            if(detla==0)break;//如果本节点已经没有残量可消耗了，就返回
        }
    }
    return flo-detla;//返回这个点已经被允许流过的流量
}
int dini()//求最大流量
{
    int ans=0;
    while(bfs())
    {
        ans+=dfs(1,INF);//用INF是因为我们不知道此时的残量到底是多少（其实这个问题还是值得想一下）
    }
    return ans;
}
//**********************************main
int main()
{
   freopen("datain.txt","r",stdin);
   datasetting();
   int a=dini();
   if(a!=0)
      if(x%a)printf("%d %d",a,(x-(x%a))/a+1);
      else printf("%d %d",a,x/a);
    else printf("Orz Ni Jinan Saint Cow!");
   return 0;
}
/********************************************************************
    ID:Andrew_82
    LANG:C++
    PROG:network-flows
********************************************************************/

优化

当然，为了提高效率，我们可以引入一个叫做cur数组的东西

不知道是哪个家伙想出来的奇技淫巧

原理是什么呢？其实就是当我们在对一个节点u（假设有6儿子）进行增广时，把他的儿子1，2，3，4的可用流量都用完了，那么在下一次dfs模块走到u时，我们如果可以直接从儿子5开始进行增广就可以大大减少额外的时间开销

具体怎么实现？

我们可以在dfs里面做一点改动，即先定义一个cur数组，在dfs之前把邻接表的head数组拷贝到cur里面，然后在遍历u的时候同时把cur里面的边的下标后移，以达到将用完的边略去的目的

代码（加cur优化）

//P1343
#include
using namespace std;
#define INF INT_MAX
const int maxn=200+5;
const int maxm=2000+5;
int n,m,x,cnt=0;
int head[maxn];
int dis[maxn];
struct node
{
    int e;
    int v;
    int nxt;
}edge[maxm<<1];
int cur[maxn];
//**********************************function
inline int read(){
   int ans=0;char r=getchar();
   while(r<'0'||r>'9')r=getchar();
   while(r>='0'&&r<='9'){ans=ans*10+r-'0';r=getchar();}
   return ans;
}
inline void addl(int u,int v,int w)
{
    edge[cnt].e=v;
    edge[cnt].v=w;
    edge[cnt].nxt=head[u];
    head[u]=cnt++;
}
void datasetting()
{
    memset(head,-1,sizeof(head));
    n=read();m=read();x=read();
    int a,b,c;
    for(int i=0;i<m;i++)
    {
        a=read();b=read();c=read();
        addl(a,b,c);addl(b,a,0);
    }
}
bool bfs()
{
    memset(dis,-1,sizeof(dis));
    dis[1]=0;
    queue<int>q;
    q.push(1);
    while(!q.empty())
    {
        int r=q.front();q.pop();
        for(int i=head[r];i!=-1;i=edge[i].nxt)
        {
            int j=edge[i].e;
            if(dis[j]==-1&&edge[i].v)
            {
                dis[j]=dis[r]+1;
                q.push(j);
            }
        }
    }
    return dis[n]!=-1;//若不可以到终点（起点）就返回false 
}
int dfs(int u,int flo)//dfs就是求节点u在残量为flo时的最大增量 
{
    if(u==n)return flo;
    int detla=flo;
    for(int i=cur[u];i!=-1;i=edge[i].nxt)
    {
        cur[u]=edge[i].nxt;
        int v=edge[i].e;
        if(dis[v]==(dis[u]+1)&&(edge[i].v)>0)
        {
            int d=dfs(v,min(detla,edge[i].v));
            edge[i].v-=d;edge[i ^ 1].v+=d;
            detla-=d;
            if(detla==0)break;
        }
    }
    return flo-detla;//返回这个点已经被允许流过的流量
}
int dini()
{
    int ans=0;
    while(bfs())
    {
        for(int i=1;i<=n;i++)cur[i]=head[i];
        ans+=dfs(1,INF);
    }
    return ans;
}
//**********************************main
int main()
{
   
   datasetting();
   int a=dini();
   if(a!=0)
      if(x%a)printf("%d %d",a,(x-(x%a))/a+1);
      else printf("%d %d",a,x/a);
    else printf("Orz Ni Jinan Saint Cow!");
   return 0;
}
/********************************************************************
    ID:Andrew_82
    LANG:C++
    PROG:network-flows
********************************************************************/

衍生问题

鲁迅说：网络流的代码只有普及组难度，建模才是最重要的

最小费用最大流问题

问题

给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

实现

由于是要求在最大流的情况下来找最小花费，容易想到的一个方法就是先求出最大流，然后用一个深搜来找到最小值

好像是可以的，但是作为一个又懒又笨的蒟蒻，我没有去试过这种方法，而且估计裸的dfs会有很大的爆栈的可能性

那么他既然要求最小花费，我们不妨把这个最小花费看成边的权值，构建一个图用最短路算法来找到源点到各个点的最短距离

找到这个数据之后，我们就可以沿着最短路来进行增广，即在最短路中求到一条可行路然后修改其残量，我们可以保证其为最大流中的一部分的最小花费

不断的进行增广直到我们找到了全部值，然后得解，这就是将dinic和spfa结合起来的求解最小费用最大流问题的方法

具体代码如下
(luoguP3381)

#include
using namespace std;
const int INF=INT_MAX;
const int maxn=5000+5,maxm=50000+5;
int n,m,s,t,cnt=0;
int head[maxn];
int dis[maxn];
int result=0;
int minfee=0;
bool vis[maxn];
struct node
{
	int e;
	int nxt;
	int w;//指权值 
	int f;//指流量 
}edge[maxm<<1];
//**********************************function
inline void addl(int u,int v,int flow,int cost)
{
	edge[cnt].e=v;
	edge[cnt].w=cost;
	edge[cnt].f=flow;
	edge[cnt].nxt=head[u];
	head[u]=cnt++;
}
inline int read()
{
   int ans=0;
   char r=getchar();
   while(r<'0'||r>'9')r=getchar();
   while(r>='0'&&r<='9')
   {
      ans=ans*10+r-'0';
      r=getchar();
   }
   return ans;
}
void datasetting()
{
	memset(head,-1,sizeof(head));
	n=read();m=read();s=read();t=read();
	int ui,vi,wi,fi;
	for(int i=0;i<m;i++)
	{
		ui=read();vi=read();wi=read();fi=read();//fi是单位流量费用，wi是最大流量 
		addl(ui,vi,wi,fi);//正向边的权值为fi，流量为wi
		addl(vi,ui,0,-fi);//反向边的权值为-fi，流量为0 
	}
}
bool spfa(int u,int v)
{
	for(int i=0;i<maxn;i++)dis[i]=INF;//spfa基本操作
	memset(vis,false,sizeof(vis));//spfa的队列排重优化
	dis[u]=0;
	deque<int>d;//spfa的slf优化
	d.push_back(u);
	vis[u]=true;
	while(!d.empty())
	{
		int ui=d.front();d.pop_front();vis[ui]=false;//ui是当前松弛的边的起点
		for(int i=head[ui];i!=-1;i=edge[i].nxt)
		{
			int vi=edge[i].e;int w=edge[i].w;int f=edge[i].f;//vi是当前松弛的边的终点 
			if(f&&dis[vi]>dis[ui]+w)//如果当前边有残量且是最短路上的边就对其进行松弛
			{
				dis[vi]=dis[ui]+w;
				if(!vis[vi])
				{
					if(!d.empty()&&dis[vi]<dis[d.front()])d.push_front(vi);
					else d.push_back(vi);
				}
			}
		}
	}
	return dis[t]!=INF;
}
int dfs(int u,int flow)
{
	if(u==t)return flow;
	int detla=flow;
	vis[u]=true;
	for(int i=head[u];i!=-1;i=edge[i].nxt)
	{
		int v=edge[i].e;int w=edge[i].w;int f=edge[i].f;
		if(f&&!vis[v]&&dis[v]==dis[u]+w)//注意，一个点只能访问一次，这个可以用vis来维护（vis在spfa模块和dfs模块中都被用到，注意初始化）
		{
			int d=dfs(v,min(f,detla));
			detla-=d;
			edge[i].f-=d;edge[i^1].f+=d;
			minfee+=d*w;//更新费用（单价x流量）
			if(detla==0)break;
		}
	}
	vis[u]=false;
	return flow-detla;
}
void dinic()
{
	result=0;
	while(spfa(s,t))
	{
		memset(vis,false,sizeof(vis));
		result+=dfs(s,INF);
	}
	printf("%d %d",result,minfee);
}
//**********************************main
int main()
{
   freopen("datain.txt","r",stdin);
   datasetting();
   dinic();
   return 0;
}
/********************************************************************
   ID:Andrew_82
   LANG:C++
   PROG:network flow
********************************************************************/

attention：

1.fi是单价，而非边权，实际的边权=流量$\times$单价

2.对于每一条可改进路，其流量都是一样的，因此在更新费用的时候就可以直接用 fi$\times$流量 了

更高级的建模参考luogu-网络流24题