python递归思想绘图

python用递归思想绘制分形几何

上上篇已经介绍了turtle的基本用法 现在给大家看一下科赫雪花的绘制

科赫雪花

科赫雪花算法介绍

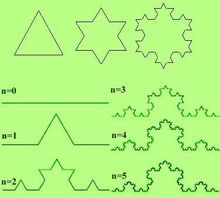
一个边长为1的等边三角形，取每边中间的三分之一，接上去一个形状完全相似的但边长为其三分之一的三角形，结果是一个六角形。取六角形的每个边做同样的变换，即在中间三分之一接上更小的三角形，以此重复，直至无穷。外界的变得原来越细微曲折，形状接近理想化的雪花。

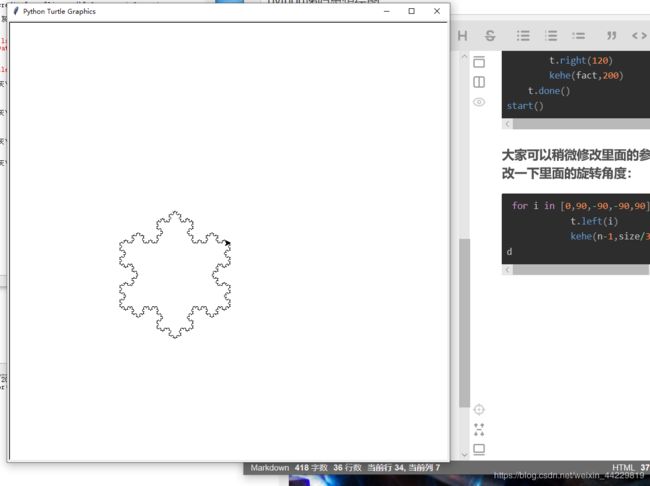
下面直接给大家看一下程序画出来的效果

import turtle as t
def kehe(n,size):
    if n==1:
        t.fd(size)
    else:
        for i in [0,60,-120,60]:
            t.left(i)
            kehe(n-1,size/3)
def start():
    t.setup(800,800)
    t.setheading(0)
    t.penup()
    t.fd(0)
    t.pendown()
    fact=5
    for i in [0,1,2]:
        t.right(120)
        kehe(fact,200)
    t.done()
start()

大家可以稍微修改里面的参数试试改一下里面的旋转角度：

or i in [0,60,-120,60]:#每次旋转的角度
            t.left(i)
            kehe(n-1,size/3)

分形几何介绍：

形几何学是一门以不规则几何形态为研究对象的几何学。相对于传统几何学的研究对象为整数维数，如，零维的点、一维的线、二维的面、三维的立体乃至四维的时空。分形几何学的研究对象为非负实数维数，如0.63、1.58、2.72、log2/log3（参见康托尔集）。因为它的研究对象普遍存在于自然界中，因此分形几何学又被称为“大自然的几何学”。一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统。分形有几种类型，可以分别依据表现出的精确自相似性、半自相似性和统计自相似性来定义。虽然分形是一个数学构造，它们同样可以在自然界中被找到，这使得它们被划入艺术作品的范畴。分形在医学、土力学、地震学和技术分析中都有应用。
[1]
简单的说，分形就是研究无限复杂具备【自相似结构的几何学】。