ABtest与Python代码
AB测试是为Web或App界面或流程制作两个(A/B)或多个(A/B/n)版本,在同一时间维度,分别让组成成分相同(相似)的访客群组(目标人群)随机的访问这些版本,收集各群组的用户体验数据和业务数据,最后分析、评估出最好版本,正式采用。而分析,评估测试结果的方法是使用统计学中的假设检验,假设检验的种类包括:t检验,Z检验,卡方检验,F检验等等。下面将基于Z检验介绍A/B测试。
AB测试步骤
- 确定要进行检验的假设
- 选择检验统计量
- 确定用于做决策的拒绝域
- 求出检验统计量的P值
- 查看样本结果是否位于拒绝域内
- 作出决策
假设检验
1. 中心极限定理和正态分布,Z检验
-
中心极限定理
样本的平均值约等于总体的平均值。不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的整体平均值周围,并且呈正态分布。
-
Z检验
Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数的差异是否显著。Z检验又叫U检验。
ABtest需要采用双样本对照的z检验公式。
Z = μ 1 − μ 2 σ 1 2 n 1 + σ 2 2 n 2 (1) Z = \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_{1}^{2}}{n_1}+\frac{\sigma_{2}^{2}}{n_2}}}\tag{1} Z=n1σ12+n2σ22μ1−μ2(1)- μ 1 \mu_1 μ1、 μ 2 \mu_2 μ2是双样本均值
- σ 1 \sigma_1 σ1、 σ 2 \sigma_2 σ2是双样本标准差
- n 1 n_1 n1、 n 2 n_2 n2是样本数目
2. H0、H1假设和显著性、置信区间、统计功效
-
H0、H1假设
根据实际问题,确定出零假设H0和备择假设H1。H0和H1互为相反,非此即彼,不可能同时满足。
例如:
- H0=A、B没有本质差异
- H1=A、B确实存在差异
检验方向的判定:
- 如果H1中包含小于号"<",则为左尾;
- 如果H1中包含大于号">",则为右尾;
- 如果H1中包含不等号"≠",则为双尾。
-
显著性
根据Z检验算出p值(查表),通常我们会用p值和0.05比较,如果p<0.05,我们就接受H0,认为AB没有显著差异。
-
置信区间
是用来对一个概率样本的总体参数进行区间估计的样本均值范围,它展现了这个均值范围包含总体参数的概率,这个概率称为置信水平。
双样本的均值差置信区间估算公式如下:
( ρ 1 − ρ 2 ) ± Z α 2 ⋅ σ 1 2 n 1 + σ 2 2 n 2 (2) (\rho_1-\rho_2)\pm Z_{\frac{\alpha}{2}}\cdot\sqrt{\frac{\sigma_{1}^{2}}{n_1}+\frac{\sigma_{2}^{2}}{n_2}}\tag{2} (ρ1−ρ2)±Z2α⋅n1σ12+n2σ22(2)- ρ 1 \rho_1 ρ1、 ρ 2 \rho_2 ρ2是双样本的观察均值
-
统计功效power
假设检验决策:
接受 H 0 H_0 H0 拒绝 H 0 H_0 H0 H 0 H_0 H0真 √ 第一类错误 H 0 H_0 H0假 第二类错误 √ -
第一类错误即在原假设正确时拒绝原假设。发生第一类错误的概率为α——即检验的显著水平(通常取5%)
-
第二类错误即在原假设错误时却接收原假设。发生第二类错误的概率用β表示
-
为了求出β,备择假设必须为一个特定数值。于是你求出检验假设域以外的数值范围,然后求出以H为条件得到这个数值范围的概率
-
功效(Power)=1-β:当所研究总体与H0确有差别时,按检验水平α能够发现它的概率(即拒绝H0,通常取0.8)。如果1-β=0.90,意味着当H0不成立时,理论上在每100次抽样中,在α的检验水准上平均有90次能够拒绝H0。
-
统计功效的计算公式如下:
P o w e r = Φ ( − Z 1 − α / 2 + Δ σ 2 / n 1 + σ 2 2 / n 2 ) (3) Power=\Phi\left (-Z_{1-\alpha/2}+\frac{\Delta}{\sqrt{\sigma^2/n_1+\sigma_2^2/n_2}}\right )\tag{3} Power=Φ(−Z1−α/2+σ2/n1+σ22/n2Δ)(3)
其中 Δ = ∣ μ 1 − μ 2 ∣ \Delta=|\mu_1-\mu_2| Δ=∣μ1−μ2∣, Φ \Phi Φ是标准正态分布的概率累积函数(CDF),有一个近似计算公式:
Φ ( x ) ≈ 1 2 { 1 + s i g n ( x ) [ 1 − e ( − 2 π x 2 ) ] 2 } (4) \Phi(x)\approx \frac{1}{2}\left \{1+sign(x)\left[1-e^{(-\frac{2}{\pi}x^2)}\right]^2 \right \}\tag{4} Φ(x)≈21{1+sign(x)[1−e(−π2x2)]2}(4)
-
流量分配
直观上说,AB即使有差异,也不一定能被你观测出来,必须保证一定的条件(比如样本要充足)才能使你能观测出统计量之间的差异;否则,结果也是不置信的。
设 n 1 = n 2 = n n_1=n_2=n n1=n2=n, σ 1 = σ 2 = σ \sigma_1=\sigma_2=\sigma σ1=σ2=σ, σ 2 \sigma^2 σ2根据经验预估,由式(3)可得:
n = 2 [ ( Z 1 − β + Z 1 − α / 2 ) ⋅ σ Δ ] 2 (5) n = 2[(Z_{1-\beta}+Z_{1-\alpha/2})\cdot\frac{\sigma}{\Delta}]^2\tag{5} n=2[(Z1−β+Z1−α/2)⋅Δσ]2(5)
以指标上为均值,如为频数,则 Δ = p 1 − p 2 \Delta=p_1-p_2 Δ=p1−p2, σ = 1 2 [ p 1 ( 1 − p 1 ) + p 2 ( 1 − p 2 ) ] \sigma=\sqrt{\frac{1}{2}[p_1(1-p_1)+p_2(1-p_2)]} σ=21[p1(1−p1)+p2(1−p2)]
python代码
1. 求实验样本量
def sample_size_u(self, a: float, b: float, u: float, s: float) -> int:
'''
已知双样本(A/B)均数,求实验样本量
:param a: alpha
:param b: beta
:param u: 均值的差值
:param s: 经验标准差
:return: 样本量
'''
n = 2 * pow(((norm.ppf(1 - a / 2) + norm.ppf(1 - b)) / (u / s)), 2)
return math.ceil(n)
def sample_size_p(self, a: float, b: float, p1: float, p2: float) -> int:
'''
已知双样本(A/B)频数,求实验样本量
:param a: alpha
:param b: beta
:param p1: 样本的频数,例如点击率50%,次日留存率80%
:param p2: 样本的频数
:return: 样本量
'''
n = pow((norm.ppf(1 - a / 2) + norm.ppf(1 - b)) / (p1 - p2), 2) * (p1 * (1 - p1) + p2 * (1 - p2))
return math.ceil(n)
2. 显著性检验
def significance_u(self, x1: float, x2: float, s1: float, s2: float, n1: int, n2: int, a: float) -> (
int, float, float):
'''
双样本双尾均值检验
:param x1: 样本均值
:param x2: 样本均值
:param s1: 样本标准差
:param s2: 样本标准差
:param n1: 样本数量
:param n2: 样本数量
:param a: alpha
:return: 显著性统计结果f,z-score, p-value
'''
z = (x1 - x2) / pow(s1 ** 2 / n1 + s2 ** 2 / n2, 1 / 2)
if z > 0:
p = (1 - norm.cdf(z)) * 2
if p < a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
else:
p = 2 * norm.cdf(z)
if p < a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
return f, format(z, '.2f'), format(p, '.2f')
def significance_p(self, p1: float, p2: float, n1: int, n2: int, a: float) -> (int, float, float):
'''
双样本双尾频数检验
:param p1: 样本频数
:param p2: 样本频数
:param n1: 样本量
:param n2: 样本量
:param a: alpha
:return: 显著性统计结果f,z-score, p-value
'''
p_pool = (n1 * p1 + n2 * p2) / (n1 + n2)
z = (p1 - p2) / pow(p_pool * (1 - p_pool) * (1 / n1 + 1 / n2), 1 / 2)
if z > 0:
p = (1 - norm.cdf(z)) * 2
if p < a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
else:
p = 2 * norm.cdf(z)
if p < a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
return f, format(z, '.2f'), format(p, '.2f')
3. 置信区间
def confidence_u(self, x1: float, x2: float, s1: float, s2: float, n1: int, n2: int, a: float) -> tuple:
'''
双样本均值检验
:param x1: 样本均值
:param x2: 样本均值
:param s1: 样本标准差
:param s2: 样本标准差
:param n1: 样本量
:param n2: 样本量
:param a: alpha
:return: 置信区间
'''
d = norm.ppf(1 - a / 2) * pow(s1 ** 2 / n1 + s2 ** 2 / n2, 1 / 2)
floor = x1 - x2 - d
ceil = x1 - x2 + d
return (format(floor, '.2f'), format(ceil, '.2f'))
def confidence_p(self, p1: float, p2: float, n1: int, n2: int, a: float) -> tuple:
'''
双样本频数检验
:param p1: 样本频数
:param p2: 样本频数
:param n1: 样本量
:param n2: 样本量
:param a: alpha
:return: 置信区间
'''
d = norm.ppf(1 - a / 2) * pow(p1 * (1 - p1) / n1 + p2 * (1 - p2) / n2, 1 / 2)
floor = p1 - p2 - d
ceil = p1 - p2 + d
return (format(floor, '.2%'), format(ceil, '.2%'))
4. 功效计算
def power_u(self, u1: float, u2: float, s1: float, s2: float, n1: int, n2: int, a: float) -> float:
'''
双样本均数检验
:param u1: 样本均值
:param u2: 样本均值
:param s1: 样本标准差
:param s2: 样本标准差
:param n1: 样本量
:param n2: 样本量
:param a: alpha
:return: 功效
'''
z = abs(u1 - u2) / pow(s1 ** 2 / n1 + s2 ** 2 / n2, 1 / 2) - norm.ppf(1 - a / 2)
b = 1 - norm.cdf(z)
power = 1 - b
return format(power, '.2%')
def power_p(self, p1: float, p2: float, n1: int, n2: int, a: float) -> float:
'''
双样本频数检验
:param p1: 样本频数
:param p2: 样本频数
:param n1: 样本量
:param n2: 样本量
:param a: alpha
:return: 功效
'''
z = abs(p1 - p2) / pow(p1 * (1 - p1) / n1 + p2 * (1 - p2) / n2, 1 / 2) - norm.ppf(1 - a / 2)
b = 1 - norm.cdf(z)
power = 1 - b
return format(power, '.2%')
5. 完整代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from scipy.stats import norm
import math
class Sample:
'''
计算样本量
https://www.abtasty.com/sample-size-calculator/
'''
def sample_size_u(self, u: float, s: float, a: float = 0.05, b: float = 0.2) -> int:
'''
已知双样本(A/B)均数,求实验样本量
:param a: alpha
:param b: beta
:param u: 均值的差值
:param s: 经验标准差
:return: 样本量
'''
n = 2 * pow(((norm.ppf(1 - a / 2) + norm.ppf(1 - b)) / (u / s)), 2)
return math.ceil(n)
def sample_size_p(self, p1: float, p2: float, a: float = 0.05, b: float = 0.2) -> int:
'''
已知双样本(A/B)频数,求实验样本量
:param a: alpha
:param b: beta
:param p1: 样本的频数,例如点击率50%,次日留存率80%
:param p2: 样本的频数
:return: 样本量
'''
n = pow((norm.ppf(1 - a / 2) + norm.ppf(1 - b)) / (p1 - p2), 2) * (p1 * (1 - p1) + p2 * (1 - p2))
return math.ceil(n)
class ABtest_u():
'''
双样本双尾均值检验
'''
def __init__(self, x1: float, x2: float, s1: float, s2: float, n1: int, n2: int, a: float = 0.05, b: float = 0.2):
self.x1 = x1 # 对照组均值
self.x2 = x2 # 测试组均值
self.s1 = s1 # 对照组标准差
self.s2 = s2 # 测试组标准差
self.n1 = n1 # 对照组样本量
self.n2 = n2 # 测试组样本量
self.a = a # alpha
self.b = b # beta
def significance_u(self) -> (int, float, float):
'''
双样本双尾均值显著性检验
'''
z = (self.x1 - self.x2) / pow(self.s1 ** 2 / self.n1 + self.s2 ** 2 / self.n2, 1 / 2)
if z > 0:
p = (1 - norm.cdf(z)) * 2
if p < self.a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
else:
p = 2 * norm.cdf(z)
if p < self.a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
return f, format(z, '.2f'), format(p, '.2f')
def confidence_u(self) -> tuple:
'''
双样本均值置信区间
'''
d = norm.ppf(1 - self.a / 2) * pow(self.s1 ** 2 / self.n1 + self.s2 ** 2 / self.n2, 1 / 2)
floor = -(self.x1 - self.x2 - d)
ceil = -(self.x1 - self.x2 + d)
return (format(floor, '.2f'), format(ceil, '.2f'))
def power_u(self) -> float:
'''
双样本均数功效
'''
z = abs(self.x1 - self.x2) / pow(self.s1 ** 2 / self.n1 + self.s2 ** 2 / self.n2, 1 / 2) - norm.ppf(
1 - self.a / 2)
b = 1 - norm.cdf(z)
power = 1 - b
return format(power, '.2%')
def main(self):
f, z, p = self.significance_u()
ci = self.confidence_u()
power = self.power_u()
print(f'保留组均值:{self.x1}')
print(f'测试组均值:{self.x2}')
print('是否显著:' + ('统计效果显著,拒绝原假设' if f == 1 else '统计效果不显著,不能拒绝原假设'))
print(f'变化度:' + format((self.x2 - self.x1) / self.x1, '.2%'))
print(f'置信区间:{ci}')
print(f'p-value:{p}')
print(f'功效:{power}')
class ABtest_p():
'''
双样本双尾频数检验
'''
def __init__(self, p1: float, p2: float, n1: int, n2: int, a: float = 0.05, b: float = 0.2):
self.p1 = p1
self.p2 = p2
self.n1 = n1
self.n2 = n2
self.a = a
self.b = b
def significance_p(self) -> (int, float, float):
'''
双样本双尾频数显著性检验
'''
p_pool = (self.n1 * self.p1 + self.n2 * self.p2) / (self.n1 + self.n2)
z = (self.p1 - self.p2) / pow(p_pool * (1 - p_pool) * (1 / self.n1 + 1 / self.n2), 1 / 2)
if z > 0:
p = (1 - norm.cdf(z)) * 2
if p < self.a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
else:
p = 2 * norm.cdf(z)
if p < self.a: # 拒绝原假设,接受备选假设
f = 1
else: # 接受原假设
f = 0
return f, format(z, '.2f'), format(p, '.2f')
def confidence_p(self) -> tuple:
'''
双样本频数置信区间
'''
d = norm.ppf(1 - self.a / 2) * pow(self.p1 * (1 - self.p1) / self.n1 + self.p2 * (1 - self.p2) / self.n2, 1 / 2)
floor = -(self.p1 - self.p2 - d)
ceil = -(self.p1 - self.p2 + d)
return (format(floor, '.2%'), format(ceil, '.2%'))
def power_p(self) -> float:
'''
双样本频数功效
'''
z = abs(self.p1 - self.p2) / pow(self.p1 * (1 - self.p1) / self.n1 + self.p2 * (1 - self.p2) / self.n2,
1 / 2) - norm.ppf(1 - self.a / 2)
b = 1 - norm.cdf(z)
power = 1 - b
return format(power, '.2%')
def main(self):
f, z, p = self.significance_p()
ci = self.confidence_p()
power = self.power_p()
print(f'保留组均值:{self.p1}')
print(f'测试组均值:{self.p2}')
print('是否显著:' + ('统计效果显著,拒绝原假设' if f == 1 else '统计效果不显著,不能拒绝原假设'))
print(f'变化度:' + format((self.p2 - self.p1) / self.p1, '.2%'))
print(f'置信区间:{ci}')
print(f'p-value:{p}')
print(f'功效:{power}')
if __name__ == '__main__':
# 计算样本量
# sample = Sample()
#
# n1 = sample.sample_size_p(p1=0.13, p2=0.14)
# print(n1)
#
# n2 = sample.sample_size_u(u=1, s=38)
# print(n2)
# 双样本双尾均值检验
# test1 = ABtest_u(x1=5.08, x2=8.04, s1=2.06, s2=2.39, n1=32058,
# n2=34515)
# test1.main()
# 双样本双尾频数检验
# test2 = ABtest_p(p1=0.4835, p2=0.5121, n1=972, n2=977)
# test2.main()
scipy.stats.norm 方法
rvs:对随机变量进行随机取值,可以通过size参数指定输出的数组的大小。
pdf:随机变量的概率密度函数
cdf:随机变量的累积分布函数,它是概率密度函数的积分
sf:随机变量的生存函数,它的值是1-cdf(t)
ppf:累积分布函数的反函数
stats:计算随机变量的期望值和方差
fit:对一组随机采样进行拟合,找出最合适取样数据的概率密度函数的系数。
示例
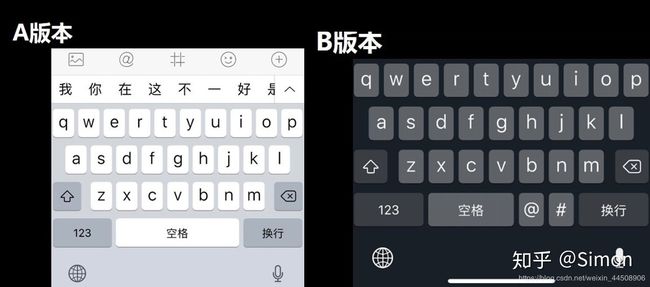
两款键盘布局不一样的手机应用(A版本,B版本),你作为公司的产品经理,想在正式发布产品之前,知道哪个键盘布局对用户体验更好?
随机抽取实验者,将实验者分成2组,A组使用键盘布局A,B组使用键盘布局B。让他们在30秒内打出标准的20个单词文字消息,然后记录打错字的数量。
问题:两种版本布局是否用户体验显著不同,哪种更好?
-
- H0:两种版本布局是否用户体验相同
H1:两种版本布局是否用户体验不同
-
数据
- 均值:x1 = 5.08,x2=8.04
- 标准差:s1 = 2.06,s2 = 2.39
- 样本量:n1 = 32058,n2 = 34515
-
代码
# 直接修改代码末尾程序入口的统计量,运行代码 test = ABtest_u(x1=5.08, x2=8.04, s1=2.06, s2=2.39, n1=32058, n2=34515) test.main() -
结果
保留组均值:5.08
测试组均值:8.04
是否显著:统计效果显著,拒绝原假设
变化度:58.27%
置信区间:(‘2.99’, ‘2.93’)
p-value:0.00
功效:100.00%在统计效果显著情况下,需判断假设检验功效,只有power >= 80%时,才能得出结论(样本量不足),否则应延长测试。
-
结论分析
-
描述统计分析
A版本打错字数量平均值:5.08个,标准差:2.06个
B版本打错字数量平均值:8.04个,标准差:2.39个
-
推论统计分析
-
假设检验
独立双样本p-value=0.00( α = 5 \alpha=5 α=5%) ,双尾检验
统计显著,拒绝零假设,接受备择假设。即:A版本和B版本打错字的均值不同,两种布局有显著差别
-
置信区间
两个独立样本均值差值的置信区间,置信水平95%,CI=(2.99, 2.93)
A版本打错字的均值小于B版本,且通过读取置信区间的数值,区间边界值均为负值,证明A版本打错字数量均值显著小于B版本,即A布局版本更符合用户体验。结论:A版本更符合用户体验
-
功效
power=100.00%,效果显著
-
-
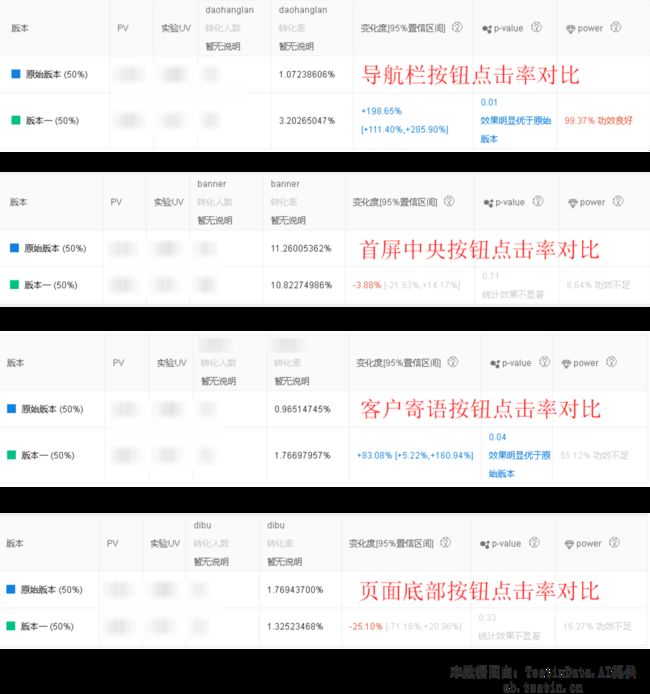
云测平台可视化案例
参考:
-
统计中的假设检验及Python实际应用
-
ABtest和假设检验、流量分配
-
如何提升3倍点击?这个AB测试告诉你答案
-
显著性检验_百度百科
-
Sample Size Calculator