PL/0语言 自下而上语法分析 SLR分析

一、简介

PL0 语言功能简单、结构清晰、可读性强，而又具备了一般高级程序设计语言的必须部分，因而 PL0 语言的编译程序能充分体现一个高级语言编译程序实现的基本方法和技术。
分析对象〈算术表达式〉的 BNF 定义如下：
<表达式> ::= [+|-]<项>{<加法运算符> <项>}
<项> ::= <因子>{<乘法运算符> <因子>}
<因子> ::= <标识符>|<无符号整数>| ‘(’<表达式>‘)’
<加法运算符> ::= +|-
<乘法运算符> ::= *|/

二、设计思想

1、表达式的文法

在上一次的自上而下分析中考虑到使用递归下降分析法，使用扩充的巴克斯范式书写表达式的文法会更简单，但是本次在LR(0)分析法中则需要转换为一般文法：
可用的文法：
E -> +B | -B | B
B -> TA | T
A -> +TA | -TA | +T | -T
T -> FM | F
M -> *FM | /FM | *F | /F
F -> i | n | (E)
不可用的文法：
E -> STA
S -> + | - |ε
A -> +TA | -TA |ε
T -> FM
M -> *FM | /FM |ε
F -> i | n | (E)

表达式开头的符号可以省略，但是后面接着的项前面的符号不可以省略；在非终结符F中，标识符和无符号整数就用终结符i和n代替。
这里要特别强调为什么我写了2种文法上去：不可用的文法不是说他错了，而是在LR分析中不可用！ 我一开始画DFA时用的就是第二个不可用文法，这个文法很好理解，也很简单。
但是，在画完LR0分析表后我发现无法正常识别表达式，原因就在于这个ε使得DFA没法正常的规约，比如开头的S要是空的话，怎么就能上来就把空规约为S呢？但事实确实得这样做。
于是我思考是不是得用LR1分析来做，于是又重新构造了一遍DFA，时间证明，不可行，一切都是ε导致的，于是我翻遍视频，书本，蛮惊讶的发现所有LR分析都没有ε的存在，我应该是知道答案了。
于是提出了可用文法，思考后我采用了SLR分析，实践证明，这次做对了。
后注：有时候有 ε 也可以用LR分析，我这个不行是因为 ε 太多了，尤其是开头哪个。
如果我的分析帮助到了你，就评论个“学霸流弊！”吧。

2、文法的项目

根据文法获得识别活前缀的方法在这里采用有效项目集来构造，为了方便表达，就不写成GO函数的形式，而是直接构造成DFA。
在构造表之前由于我使用的是SLR分析，所以需要先做好开始条件。
文法的表达式编号：
1：E -> +B
2：E -> -B
3：E -> B
4：B -> TA
5：B -> T
6：A -> +TA
7：A -> -TA
8：A -> +T
9：A -> -T
10：T -> FM
11：T -> F
12：M -> *FM
13：M -> /FM
14：M -> *F
15：M -> /F
16：F -> i
17：F -> n
18：F -> (E)
FIRST和FOLLOW集合：
为方便表示，我将读入的标识符和整数用终结符i和n表示

—	FIRST	FOLLOW
E	+ - i n (	# )
B	i n (	# )
T	i n (	# + - )
A	+ -	# )
F	i n (	# + - * / )
M	* /	# + - )

3、DFA

由于状态太多，所以我只画了识别非终结符的线条，识别终结符的线条没有画出来，详情参考下面的ACTION表。

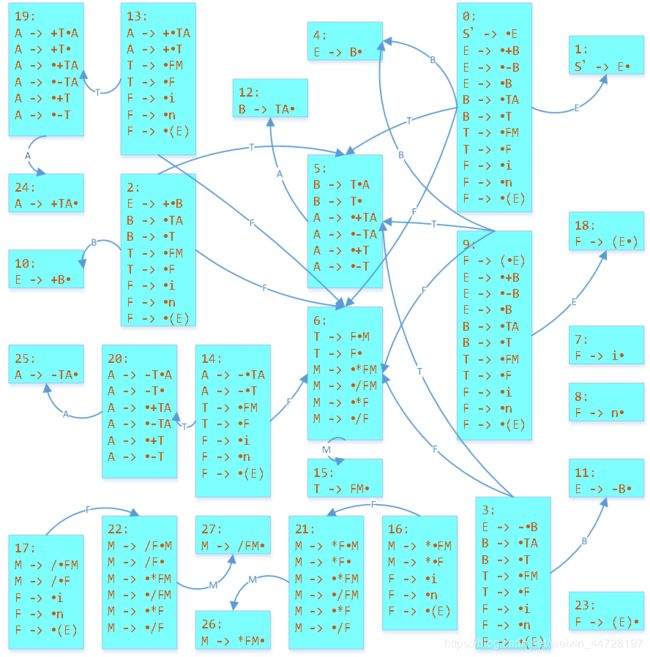
4、SLR分析表

对表格中所有空格致ERROR出错标志。
其中的规约项并不是像LR0分析一样一整行都是，经过分析后认为无需画LR1分析表。
所有的规约项目都是参照FOLLOW集合来添加，不然会产生冲突。

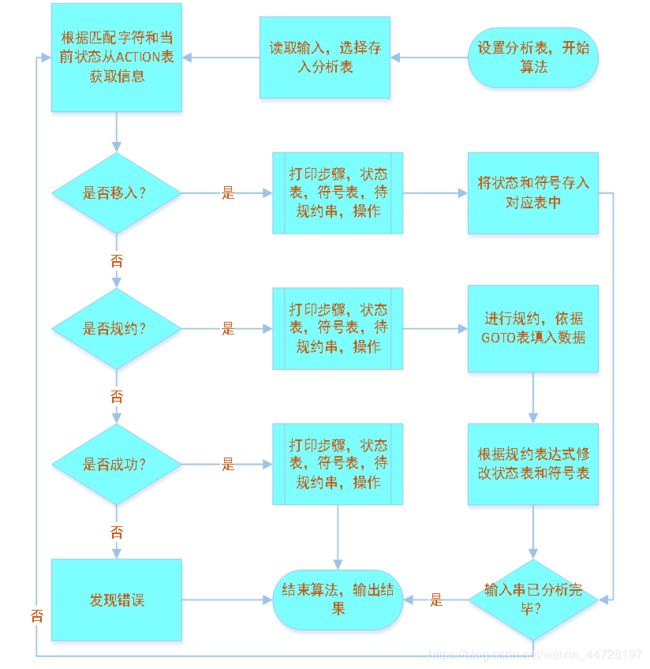
三、算法流程

算法的流程图就是对各种单词符号的组合进行判断。
对于输入的种别编码采用首字母存储，这杨就和符号都可以统一以字符来处理。

四、源程序

#include 
#include
#include
#include//函数atoi头文件
using namespace std;

string get_action(string temp);//获取ACTION表中单元格的字符串（S/R/ACC/ERR）
int get_action_num(string temp);//获取ACTION表中单元格后的数字，ACC为0，ERR为-1
void print_access();//打印分析步骤
void input_string();//通过表达式字符串进行输入
void input_word_analysis();//从词法分析的结果获得输入
void SLR_analysis();//分析过程函数

string ACTION[28][9]={//ACTION表
{"S2" ,"S3" ,"ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","ERR","ACC"},
{"ERR","ERR","ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"ERR","ERR","ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","R3" ,"R3" },
{"S13","S14","ERR","ERR","ERR","ERR","ERR","R5" ,"R5" },
{"R11","R11","S16","S17","ERR","ERR","ERR","R11","R11"},
{"R16","R16","R16","R16","ERR","ERR","ERR","R16","R16"},
{"R17","R17","R17","R17","ERR","ERR","ERR","R17","R17"},
{"S2" ,"S3" ,"ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","R1" ,"R1" },
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","R2" ,"R2" },
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","R4" ,"R4" },
{"ERR","ERR","ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"ERR","ERR","ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"R10","R10","ERR","ERR","ERR","ERR","ERR","R10","R10"},
{"ERR","ERR","ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"ERR","ERR","ERR","ERR","S7" ,"S8" ,"S9" ,"ERR","ERR"},
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","S23","ERR"},
{"S13","S14","ERR","ERR","ERR","ERR","ERR","R8" ,"R8" },
{"S13","S14","ERR","ERR","ERR","ERR","ERR","R9" ,"R9" },
{"R14","R14","S16","S17","ERR","ERR","ERR","R14","R14"},
{"R15","R15","S16","S17","ERR","ERR","ERR","R15","R15"},
{"R18","R18","R18","R18","ERR","ERR","ERR","R18","R18"},
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","R6" ,"R6" },
{"ERR","ERR","ERR","ERR","ERR","ERR","ERR","R7" ,"R7" },
{"R12","R12","ERR","ERR","ERR","ERR","ERR","R12","R12"},
{"R13","R13","ERR","ERR","ERR","ERR","ERR","R13","R13"}};
int GOTO[28][6]={//GOTO表
{1,4,5,0,6,0},
{0,0,0,0,0,0},
{0,10,5,0,6,0},
{0,11,5,0,6,0},
{0,0,0,0,0,0},
{0,0,0,12,0,0},
{0,0,0,0,0,15},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{18,4,5,0,6,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,19,0,6,0},
{0,0,20,0,6,0},
{0,0,0,0,0,0},
{0,0,0,0,21,0},
{0,0,0,0,22,0},
{0,0,0,0,0,0},
{0,0,0,24,0,0},
{0,0,0,25,0,0},
{0,0,0,0,0,26},
{0,0,0,0,0,27},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0}};

int step=1;//分析的步骤计数
int length=0;//输入串的长度
int state[100]={0};//状态表
char ch[100]={'#'};//符号表
int l=0;//状态表或符号表当前字符位置
char str[100];//输入串
int k=0;//输入串中当前面临的字符，即指向待匹配字符
int num;//ACTION表中的数字
string how;//ACTION表中的字符串

string get_action(string temp)//获取ACTION表中单元格的字符串（S/R/ACC/ERR）
{
    if(temp=="ACC")return temp;
    else if(temp=="ERR")return temp;
    else return temp.substr(0,1);//返回下标从0开始长度为1的字符串，即S或者R
}
int get_action_num(string temp)//获取ACTION表中单元格后的数字，ACC为0，ERR为-1
{
    if(temp=="ACC")return 0;
    else if(temp=="ERR")return -1;
    else{
        string num=temp.substr(1);//返回下标从1开始到结尾的字符串，转换为整型
        return atoi(num.c_str());
    }
}

void print_access()//打印分析步骤
{
	int i;
    printf("%d\t",step);//输出第几步
    for(i=0;i<=l;i++)//输出状态表
    {
        printf("%d ",state[i]);
    }
    if(l>=3) printf("\t");
    else printf("\t\t");
    for(i=0;i<=l;i++)//输出符号表
    {
        printf("%c",ch[i]);
    }
    printf("\t\t");
    for(i=0;i<k;i++)//输出几个空格
    {
        str[i]=' ';
        printf("%c",str[i]);
    }
    for(i=k;i<length;i++)//输出待规约字符串
    {
        printf("%c",str[i]);
    }
    printf("\t");
}

void input_string()//通过表达式字符串进行输入
{
    printf("请输入表达式字符串:");
	char ch;
    do
    {
        scanf("%c",&ch);
        str[length]=ch;
        length++;
    }while(ch!='#');//以表达式输入时以#结尾
}

void input_word_analysis()//从词法分析的结果获得输入
{
    int count=7;//输入有7行
    while(count-->0)
    {
        string temp;
        cin>>temp;
        int word_begin=temp.find(',');//找到单词符号的结尾
        string keyword=temp.substr(1,word_begin-1);//将单词符号截取出来，去掉无用字符
        if(keyword=="ident")str[length]='i';//把标识符设置为i
        else if(keyword=="number")str[length]='n';//把整数设置为n
        else
        {
            string symbol=temp.substr(word_begin+1,word_begin+1);//截取符号：+ - * / ( )
            str[length]=symbol.c_str()[0];
        }
        length++;
    }
    str[length]='#';
    length++;
}

void SLR_analysis()//分析过程函数
{
	do
    {
		int j;
        switch(str[k])//获取待规约串第一个字符
        {
            case '+': j=0;break;//转换为数字方便查表
            case '-': j=1;break;
            case '*': j=2;break;
            case '/': j=3;break;
            case 'i': j=4;break;
            case 'n': j=5;break;
            case '(': j=6;break;
            case ')': j=7;break;
            case '#': j=8;break;
            default: j=-1;break;
        }
        if(j!=-1)
        {
            string action=ACTION[state[l]][j];//获取ACTION表中信息
            how=get_action(action);//获取操作方式
            num=get_action_num(action);//获取数字
            if(how=="S")
            {
                print_access();
                printf("压入状态 %d!\n",num);
                l=l+1;
                state[l]=num;//添加状态
                ch[l]=str[k];//添加字符
                step=step+1;
                k=k+1;//指向下一待匹配的字符
            }
            else if(how=="R")
            {
                char push_sign;//规约形成的新非终结符
				int back_step;//规约时要删除的字符数
                print_access();
                switch(num)//num是用第几个产生式做规约
                {
                    case 1:
                        push_sign='E',back_step=2;//保存规约后字符以及需要回退的格数
                        l=l-back_step;
                        printf("E -> +B");
                        break;
                    case 2:
                        push_sign='E',back_step=2;
                        l=l-back_step;
                        printf("E -> -B");
                        break;
                    case 3:
                        push_sign='E',back_step=1;
                        l=l-back_step;
                        printf("E -> B");
                        break;
                    case 4:
                        push_sign='B',back_step=2;
                        l=l-back_step;
                        printf("B -> TA");
                        break;
                    case 5:
                        push_sign='B',back_step=1;
                        l=l-back_step;
                        printf("B -> T");
                        break;
                    case 6:
                        push_sign='A',back_step=3;
                        l=l-back_step;
                        printf("A -> +TA");
                        break;
                    case 7:
                        push_sign='A',back_step=3;
                        l=l-back_step;
                        printf("A -> -TA");
                        break;
                    case 8:
                        push_sign='A',back_step=2;
                        l=l-back_step;
                        printf("A -> +T");
                        break;
                    case 9:
                        push_sign='A',back_step=2;
                        l=l-back_step;
                        printf("A -> -T");
                        break;
                    case 10:
                        push_sign='T',back_step=2;
                        l=l-back_step;
                        printf("T -> FM");
                        break;
                    case 11:
                        push_sign='T',back_step=1;
                        l=l-back_step;
                        printf("T -> F");
                        break;
                    case 12:
                        push_sign='M',back_step=3;
                        l=l-back_step;
                        printf("M -> *FM");
                        break;
                    case 13:
                        push_sign='M',back_step=3;
                        l=l-back_step;
                        printf("M -> /FM");
                        break;
                    case 14:
                        push_sign='M',back_step=2;
                        l=l-back_step;
                        printf("M -> *F");
                        break;
                    case 15:
                        push_sign='M',back_step=2;
                        l=l-back_step;
                        printf("M -> /F");
                        break;
                    case 16:
                        push_sign='F',back_step=1;
                        l=l-back_step;
                        printf("F -> i");
                        break;
                    case 17:
                        push_sign='F',back_step=1;
                        l=l-back_step;
                        printf("F -> n");
                        break;
                    case 18:
                        push_sign='F',back_step=3;
                        l=l-back_step;
                        printf("F -> (E)");
                        break;
                }
                int n;
                switch(push_sign)//把要压入的非终结符换成数字
                {
                    case 'E': n=0;break;
                    case 'B': n=1;break;
                    case 'T': n=2;break;
                    case 'A': n=3;break;
                    case 'F': n=4;break;
                    case 'M': n=5;break;
                }
                num=GOTO[state[l]][n];//此时num为压入的状态
                printf("，压入 %d!\n",num);
                l=l+1;
                state[l]=num;//这里是修改了两个表特定位置的内容，对于大于l处的内容无需删除，只要用l控制好边界即可
                ch[l]=push_sign;
                step=step+1;
            }
            else if(how=="ACC")
            {
                print_access();
                printf("ACC!\n");
                printf("Yes,it is correct.\n");
                return;
            }
            else
            {
                printf("No,it is wrong.\n");
                return;
            }
        }
        else
        {
            //printf("错误的输入字符!\n");
            printf("No,it is wrong.\n");
            return;
        }
    }while(str[k]!='\0');
}

int main()
{
    input_string();//直接读入表达式，如+(i+n-(i*(i-i)))*i#
    //input_word_analysis();//从词法分析的结果获得输入
    printf("\n--------------------------------------------------------------------------\n");
    printf("step\tstate\t\tcharacter\tstring\t\taction\n");
    printf("--------------------------------------------------------------------------\n");
    SLR_analysis();
    return 0;
}

这个得等老师截止提交后我才能发出来，不然就代码雷同了。。。。
我晕，这老师隔了好久还查之前的代码，为了防止我中枪我把前两次的设为私密了，如果有不会的地方可以留言提问我。

五、数据测试

说明：
1、上面的代码是带有分析过程的代码，去掉各种输出就是提交的代码。
2、算法有2种输入方式，一是直接输入表达式，二是输入词法分析的结果。
输入输出示例1：
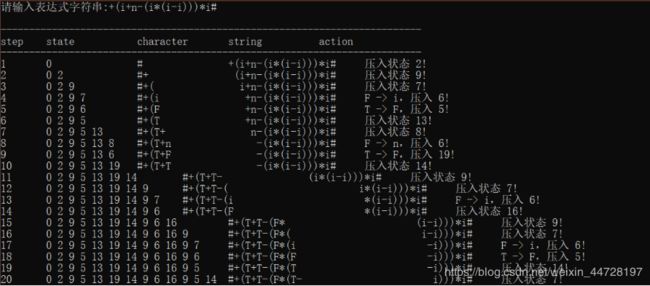
以词法分析的结果作为输入，带有分析过程。

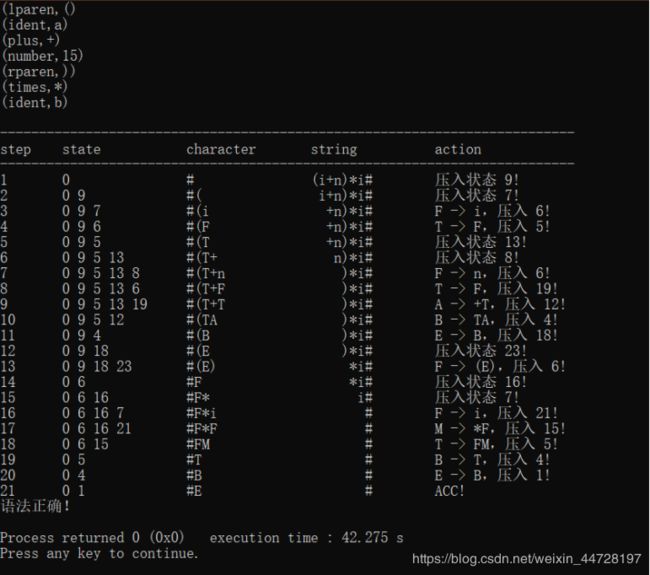
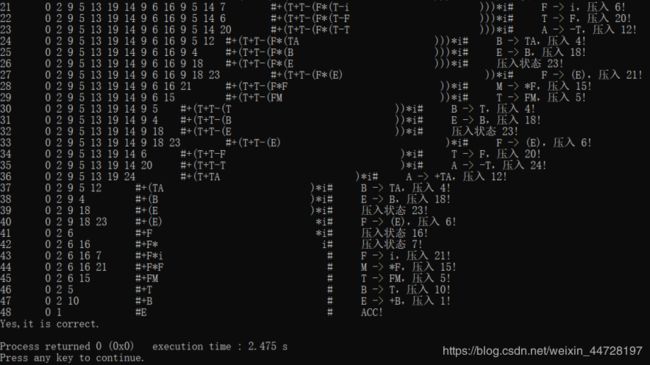
输入输出示例2：
以表达式方式输入，输入：+(i+n-(i*(i-i)))*i# 带有分析过程。