数据结构基础—Python3实现二叉搜索树(删除二叉搜索树中的节点)
实现以下内容:
BST :二叉搜索树
- BST 前序遍历的非递归写法
- BST 的广度优先遍历
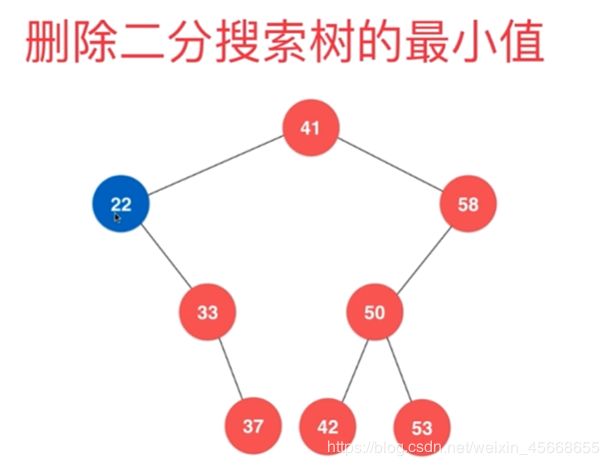
- BST 中的最小值
- BST 中的最大值
- 删除BST 中的最小值
- 删除BST中的最大值
- 删除BST中的任意元素(利用5、6)
BST的前序遍历非递归写法,利用栈的性质(后入先出),模拟一个栈
BST的广度优先遍历,利用队列的性质(先入先出),模拟一个队列
# Python中没有栈,我们需要模拟一个栈
class Stack():
def __init__(self):
self.items = []
def push(self,e):
self.items.append(e)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[-1]
def isEmpty(self):
return len(self.items) == 0
def size(self):
return len(self.items)
def __repr__(self):
return str(self.items)
class Queue():
def __init__(self):
self.items = []
def enqueue(self,e):
self.items.append(e)
def dequeue(self):
self.items.remove(self.items[0])
def isEmpty(self):
return (len(self.items) == 0)
def getFront(self):
return self.items[0]
1.BST 的前序遍历非递归写法
def preTraverse(self):
stack = Stack()
stack.push(self.__root)
while not stack.isEmpty():
curr = stack.pop()
print(curr.e)
if curr.right != None:
stack.push(curr.right)
if curr.left != None:
stack.push(curr.left)
2.BST的广度优先遍历(层序遍历)
def levelOrder(self):
queue = Queue()
queue.enqueue(self.__root)
while not queue.isEmpty():
curr = queue.dequeue()
print(curr.e)
if curr.left != None:
queue.enqueue(curr.left)
if curr.right != None:
queue.enqueue(curr.right)
3.BST 中的最小值
二叉搜索树的性质:最小值在左子树中
def findMin(self):
if self.__root == None:
return ("BST is empty!")
return self.__findMin(self.__root).e
def __findMin(self,node):
#终止条件
if node.left == None:
return node
return self.__findMin(node.left)
4.BST 中的最大值
# 寻找最大值的递归写法
def findMax(self):
if self.__root == None:
return ("BST is empty")
return self.__findMax(self.__root).e
def __findMax(self,node):
#终止条件
if node.right == None:
return node
return self.__findMax(node.right)
5.删除BST中的最小值
考虑两种情况
def delMin(self):
#利用之前写的函数找到最小值
ret = self.findMin()
self.__root = self.__delMin(self.__root)
return ret
def __delMin(self,node):
#终止条件:当树的左子树为空时
if node.left == None:
#此时最小值可能还有右子树
rightNode = node.right
node.right = None
self.__size -= 1
return rightNode
node.left = self.__delMin(node.left)
return node
6.删除BST中的最大值
跟删除最小值的思路是一样的
#删除树中最大值并返回
def delMax(self):
ret = self.findMax()
self.__root = self.__delMax(self.__root)
return ret
def __delMax(self,node):
#终止条件
if node.right == None:
leftNode = node.left
node.left = None
self.__size -= 1
return leftNode
node.right = self.__delMax(node.right)
return node
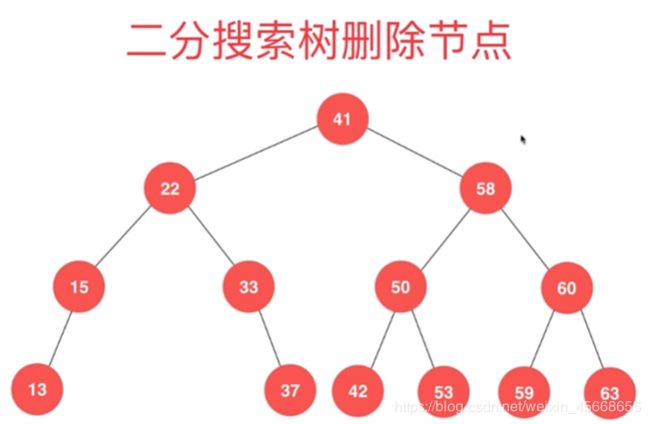
删除BST的任意一个元素
思路:
- 判断树是否为空
- 如果用户传入的元素比根节点大,在右子树中删除
- 如果用户传入的元素比根节点小,在左子树中删除
- 找到待删除的节点,此时还要分为三种情况:
- 当待删除节点的左子树为空
- 当待删除的节点的右子树为空
- 当待删除的节点的左右子树都不为空(选择用待删除节点的右子树的最小值 代替删除后的节点),如下图所示:
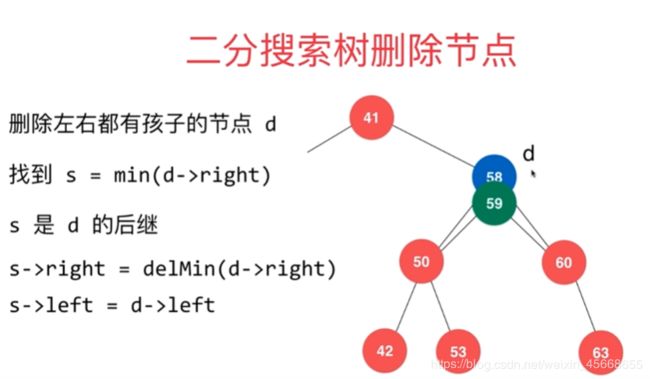
(上图中,要删除节点58, 59是58在右子树中的最小值,记录最小值,然后删除这个最小值,最后给59的左右子树赋值)
def remove(self,e):
self.__root = self.__remove(self.__root,e)
#删除以node为根的二分搜索树中值为e的节点,递归算法
# 返回删除节点后新的二分搜索树的根
def __remove(self,node,e):
#终止条件
if node == None:
return None
if e < node.e:
node.left = self.__remove(node.left,e)
return node
elif e > node.e:
node.right = self.__remove(node.right,e)
return node
else:
# node.e == e
# 待删除元素左子树为空
if node.left == None:
rightNode = node.right
node.right = None
self.__size -= 1
return rightNode
# 待删除元素右子树为空
if node.right == None:
leftNode = node.left
node.left = None
self.__size -= 1
return leftNode
# 待删除元素左右子树都不为空
# 找到比待删除节点大的最小节点,(待删除节点右子树的最小节点)
# 用这个节点顶替待删除节点的位置
successor = self.__findMin(node.right)
successor.right = self.__delMin(node.right)
successor.left = node.left
node.left = node.right = None
return successor
代码测试:
bst = BST()
nums = [41,22,58,15,33,50,60,13,37,42,53,59,63]
for i in nums:
bst.add(i)
bst.remove(58) # 删除左右子树都有的节点
bst.remove(13)
bst.remove(41)
bst.preOrder()
输出结果为:
42
22
15
33
37
59
50
53
60
63