最适合小白的matlab教程系列_进阶系列二之多项式
多项式
- 一维插值
- 二维插值
- 计算多项式
- *计算多项式*
- 计算多项式乘除法
- 多项式求导
- 多项式求积分
- 多项式曲线拟合
一维插值
命名格式vq=interp1(x,v,xq)
x:原始数据(自变量)n维向量
v:原始数据(函数值)n维向量
xq:插值(自变量)可以是一个点,可以是向量
vq:插值结果(函数值)
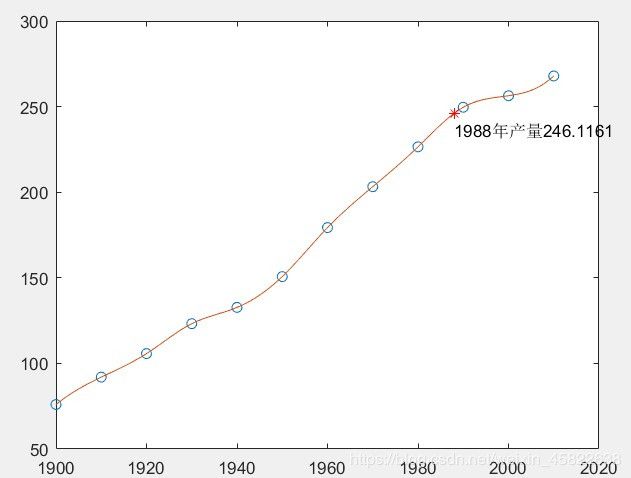
years=1900:10:2010;
production=[75.995,91.972,105.711,123.203,132.699,150.697,...
179.323,203.212,226.505,249.633,256.344,267.893];
p1988=interp1(years,production,1988,'spline')
x=1900:2010;
y=interp1(years,production,x,'spline');
plot(years,production,'o',x,y);
hold on
plot(1988,p1988,'*r')
text(1988,p1988-10,['1988年产量',num2str(p1988)])| method | description | 需要点数 | 内存占用 | 计算时间 |
|---|---|---|---|---|
| linear | 线性插值 | 至少2个 | 较多 | 稍长 |
| nearest | 最邻近点插值 | 至少2个 | 少 | 短 |
| next | 下一个临近点插值 | 至少2个 | 少 | 短 |
| previous | 前一个临近点插值 | 至少2个 | 少 | 短 |
| pchip | 保型插值 | 至少4个 | 多 | 较长 |
| spline | 三次样条插值 | 至少4个 | 较多 | 最长 |
x=0:2:24;
y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
xi=0:1/3600:24;
strmethod={'nearest','linear','next','previous','spline','pchip'};
strlb={'(a)method=nearest','(b)method=linear','(c)method=next','(d)method=previous','(e)method=spline','(f)method=pchip'};
for i=1:6
yi=interp1(x,y,xi,strmethod(i));
subplot(3,2,i)
plot(x,y,'ro',xi,yi,'b','linewidth',1.5),xlabel(strlb(i))
end
为了比较花在一个图里 hold on一下就可以了。
x=0:2:24;
y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
xi=0:1/3600:24;
strmethod={'nearest','linear','next','previous','spline','pchip'};
strcolor={'y','g','c','b','m','r'};
for i=1:6
yi=interp1(x,y,xi,strmethod{i});
plot(xi,yi,strcolor{i},'linewidth',5-0.5*i)
hold on
end
plot(x,y,'ko','linewidth',5)
legend( '(a)method=nearest','(b)method=linear','(c)method=next',...
'(d)method=previous','(e)method=spline','(f)method=pchip',...
'origianl data ');二维插值
命名格式
vi=interp2(x,y,v,xi,yi)
vi=interp2(x,y,v,xi,yi,method)
vi=interp2(v,n)例题
创建一个粗糙的山顶曲面通过二维插值做出更精细的山顶曲面
clear all;clc ; close all;
%粗糙山顶曲面
[X,Y]=meshgrid(-3:3);
V=peaks(X,Y);
figure
surf(X,Y,V)
%精细山顶曲面
[Xq,Yq]=meshgrid(-3:0.23:3);
Vvq=interp2(X,Y,V,Xq,Yq);
figure
surf(X1,Yq,Vq)在例题1的基础上使用vi=interp2(v,n)命令完成二位插值
clear all;clc;close all;
[X,Y]=meshgrid(-3:3);
V=peaks(X,Y);
figure
surf(X,Y,V)
title('Original Sampling');
figure
Vq=interp2(V,2);%作两次递归计算
surf(Vq)三维插值
命名格式
Vq=interp3(X,Y,Z,V,Xq,Yq,Zq)
Vq=interp3(X,Y,Z,V,Xq,Yq,Zq,method)
Vq=interp3(V,K)
例题
创建一个粗糙的切面图,通过三维插值作出更精细的切面图
clear all;clc;close all;
[X,Y,Z,V]=flow(10);%提供可视化的标量数据
figure;
slice(X,Y,Z,V,[5,9],2,[-2,2]);%在X=5,9,Y=2,Z=-2,2无处位置取切面
%slice 四维作图
shading flat
[Xq,Yq,Zq]=meshgrid(.1:.25:10,-3:.25:3,-3:.25:3);
Vq=interp3(X,Y,Z,V,Xq,Yq,Zq);
figure
slice(Xq,Yq,Zq,Vq,[5 9],2,[-2 2]);
shading flat %图片的设定计算多项式
命名格式
y=polyval(p,x)
y=p1xn+p2xn-1+…pnx+pn+1
x:可以是标量也可以是矩阵
实例分析
p(x)=2x^4 +x^3 -9x^2 +6在x=3的值
>> p=[2 1 -9 0 6];
>> x=3;
>> p_3=polyval(p,x)
>p_3 =
114计算多项式
命名格式p=poly(r)
r:多项式的根
计算多项式的系数,实例分析
例题
>> p=[2 1 -9 0 6];
>> r=roots(p);
>> p=poly(r)
p =
1.0000 0.5000 -4.5000 0.0000 3.0000计算多项式乘除法
conv(p1,p2) %多项式乘法
[q,r]=deconv(p1,p2) %多项式除法
实例分析
p1(x)=x^2+3x+5
,p2(x)=x^2+4x-2
求p1p2乘积(答案:x4+7x3+15x^2+14x-10)
>> p1=[1 3 5];
>> p2=[1 4 -2];
>> prod=conv(p1,p2)
prod =
1 7 15 14 -10
p1(x)=x^2-9x-10 p2(x)=x+1 求p1p2的商和余数
>>p1=[1 -9 -10];
>>p2=[1 1];
>>[q,r]=deconv(p1,p2)
q=1 -1 0
r=0 0 0多项式求导
dp=polyder(p) %多项式p求导
dp=polyder(a,b) %多项式a,b乘积的导数
例题
求p(x)=2x4+x3-9x^2+6的导数
p=[2 1 -9 0 6];
dp=polyder(p)
dp= 8 3 -18 0例题2;p1(x)=x^2+6,p2(x)=3x+1的乘积的导数
>> p1=[1 0 6];
>> p2=[3 1];
>> dp=polyder(p1,p2)
dp =
9 2 18
多项式求积分
polyint(p,k)
polyint§
k:加入常数项
例题 实例分析
p(x)=9x^2+2x+18的积分 加入常数项k=23
>> p=[ 9 2 18];
>> p_inv=polyint(p,23)
p_inv =
3 1 18 23多项式
poly2str(p,'s') %用字符串形式表达多项式
poly2sym(p,'s') %用符号形式表达该多项式
多项式曲线拟合
p=polyfit(x,y,n)
[p,S]=polyfit(x,y,n)
x:采样点
y:采样点函数值
n:多项式阶数
S:预测值的误差估计
例题:根据要求找到合适的多项式(最大残差莫不超过10^-4
clear all;clc ; close all;
%采样点
x=[0:pi/4:2*pi];
y=sin(x);
%%多项式曲线拟合
[p,S]=polyfit(x,y,5);%s包含 R:系数矩阵的QR分解的上三角阵 df:自由度 normr:最大残差模
x1=[0:pi/10:2*pi];%比用x光滑
p_x=polyval(p,x1);
%绘图
plot(x,y,'ro','linewidth',1.5)
xlabel('x'),ylabel('y=sin(x)')
hold on
plot(x1,p_x,'b','linewidth',1.5)
legend('y(x)','p(x)')
hold off