LeetCode-难题集之Implement strStr()与KMP算法

 Implement strStr():https://leetcode.com/problems/implement-strstr/

Implement strStr().

Returns the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.

这道题不难但引出了KMP算法，这个是一个难理解的算法，先看看此题的三种解法接着介绍KMP算法。

Brute-force version

class Solution {
public:
    int strStr(string haystack, string needle) {
        int i, hSize = haystack.size(), nSize = needle.size();
        if(hSize

Robin-Karp version 

class Solution{
	public:
		int strStr(string haystack,string needle){
		    if(needle=="")return 0;
			for(int i=0;ihaystack.size())return -1;
				if(needle[0]==haystack[i]){
					int j=0;
					while(j

Standard KMP algorithm

class Solution {
    private:
        void buildKMPTable(const string & s, vector &KMP_Table)
        {
            int sSize = s.size(), i=2, j=0;
            KMP_Table[0] = -1;
            if(sSize>1) KMP_Table[1] = 0;
            while(i0) j = KMP_Table[j];
                else KMP_Table[i++] = 0;
            }
        }
    public:
        int strStr(string haystack, string needle) {
            int start=0, i=0, hSize = haystack.size(), nSize = needle.size();
            if(hSize KMP_Table(nSize, 0);
            buildKMPTable(needle, KMP_Table);
            while(start<=hSize-nSize)
            {
                if(haystack[start+i]==needle[i])
                {
                    if(++i == nSize) return start;
                }
                else
                {
                    start = start+i-KMP_Table[i];
                    i= i>0?KMP_Table[i]:0;    
                }
            }
            return -1;
        }
    };

KMP算法

原文链接：http://www.tuicool.com/articles/e2Qbyyf

如果你看不懂 KMP 算法，那就看一看这篇文章 ( 绝对原创，绝对通俗易懂 )

KMP 算法，俗称“看毛片”算法，是字符串匹配中的很强大的一个算法，不过，对于初学者来说，要弄懂它确实不易。整个寒假，因为家里没有网，为了理解这个算法，那可是花了九牛二虎之力！不过，现在我基本上对这个算法理解算是比较透彻了！特写此文与大家分享分享！

我个人总结了， KMP 算法之所以难懂，很大一部分原因是很多实现的方法在一些细节的差异。怎么说呢，举我寒假学习的例子吧，我是看了一种方法后，似懂非懂，然后去看另外的方法，就全都乱了！体现在几个方面： next 数组，有的叫做“失配函数”，其实是一个东西； next 数组中，有的是以下标为 0 开始的，有的是以 1 开始的； KMP 主算法中，当发生失配时，取的 next 数组的值也不一样！就这样，各说各的，乱的很！

所以，在阐述我的理解之前，我有必要说明一下，我是用 next 数组的， next 数组是以下标 0 开始的！还有，我不会在一些基础的概念上浪费太多，所以你在看这篇文章时必须要懂得一些基本的概念，例如 “ 朴素字符串匹配 ”“ 前缀 ” ， “ 后缀 ” 等！还有就是，这篇文章的每一个字都是我辛辛苦苦码出来的，图也是我自己画的！如果要转载，请注明出处！好了，开始吧！

假设在我们的匹配过程中出现了这一种情况：

根据 KMP 算法，在该失配位会调用该位的 next 数组的值！在这里有必要来说一下next 数组的作用！说的太繁琐怕你听不懂，让我用一句话来说明：

返回失配位之前的最长公共前后缀！

好，不管你懂不懂这句话，我下面的文字和图应该会让你懂这句话的意思以及作用的！

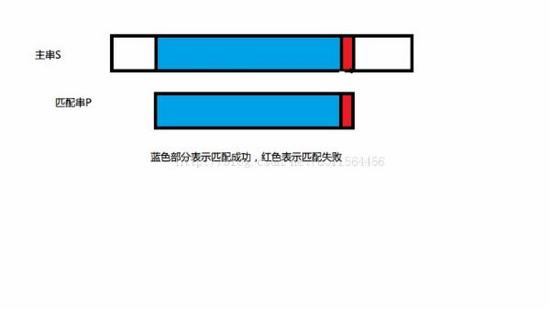
首先，我们取之前已经匹配的部分（即蓝色的那部分！）

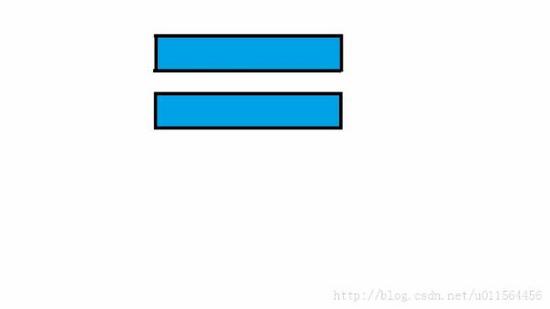
我们在上面说到 next 数组的作用时，说到 “ 最长公共前后缀 ” ，体现到图中就是这个样子！

接下来，就是最重要的了！

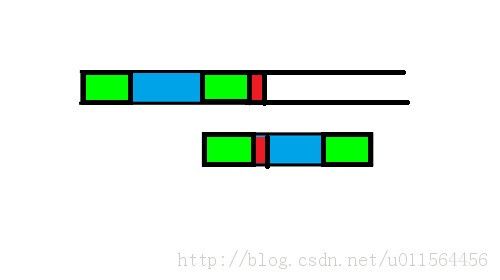
没错，这个就是 next 数组的作用了 :

返回当前的最长公共前后缀长度，假设为 len 。因为数组是由 0 开始的，所以 next数组让第 len 位与主串匹配就是拿最长前缀之后的第 1 位与失配位重新匹配，避免匹配串从头开始！如下图所示！

（重新匹配刚才的失配位！）

 /-

"前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

以”ABCDABD”为例，进行介绍：
－　”A”的前缀和后缀都为空集，共有元素的长度为0；
－　”AB”的前缀为[A]，后缀为[B]，共有元素的长度为0；
－　”ABC”的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；
－　”ABCD”的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；
－　”ABCDA”的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为”A”，长度为1；
－　”ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为”AB”，长度为2；
－　”ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

-/

如果都说成这样你都不明白，那么你真的得重新理解什么是 KMP 算法了！

 

接下来最重要的，也是 KMP 算法的核心所在，就是 next 数组的求解！不过，在这里我找到了一个全新的理解方法！如果你懂的上面我写的的，那么下面的内容你只需稍微思考一下就行了！

 

跟刚才一样，我用一句话来阐述一下 next 数组的求解方法，其实也就是两个字：

继承

a 、当前面字符的前一个字符的对称程度为 0 的时候，只要将当前字符与子串第一个字符进行比较。这个很好理解啊，前面都是 0 ，说明都不对称了，如果多加了一个字符，要对称的话最多是当前的和第一个对称。比如 agcta 这个里面 t 的是 0 ，那么后面的 a 的对称程度只需要看它是不是等于第一个字符 a 了。

b 、按照这个推理，我们就可以总结一个规律，不仅前面是 0 呀，如果前面一个字符的 next 值是 1 ，那么我们就把当前字符与子串第二个字符进行比较，因为前面的是1 ，说明前面的字符已经和第一个相等了，如果这个又与第二个相等了，说明对称程度就是 2 了。有两个字符对称了。比如上面 agctag ，倒数第二个 a 的 next 是 1 ，说明它和第一个 a 对称了，接着我们就把最后一个 g 与第二个 g 比较，又相等，自然对称成都就累加了，就是 2 了。  

c 、按照上面的推理，如果一直相等，就一直累加，可以一直推啊，推到这里应该一点难度都没有吧，如果你觉得有难度说明我写的太失败了。

当然不可能会那么顺利让我们一直对称下去，如果遇到下一个不相等了，那么说明不能继承前面的对称性了，这种情况只能说明没有那么多对称了，但是不能说明一点对称性都没有，所以遇到这种情况就要重新来考虑，这个也是难点所在。

如果蓝色的部分相同，则当前 next 数组的值为上一个 next 的值加一，如果不相同，就是我们下面要说的！

如果不相同，用一句话来说，就是：

从前面来找子前后缀

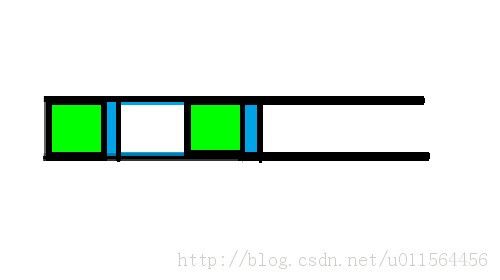
1 、如果要存在对称性，那么对称程度肯定比前面这个的对称程度小，所以要找个更小的对称，这个不用解释了吧，如果大那么就继承前面的对称性了。

2 、要找更小的对称，必然在对称内部还存在子对称，而且这个必须紧接着在子对称之后。

 

如果看不懂，那么看一下图吧！

好了，我已经把该说的尽可能以最浅显的话和最直接的图展示出来了，如果还是不懂，那我真的没有办法了！

说了这么多，下面是代码实现

#include 
#include 
#include 
#define N 100

void cal_next( char * str, int * next, int len )
{
  int i, j;

  next[0] = -1;
  for( i = 1; i < len; i++ )
  {
    j = next[ i - 1 ];
    while( str[ j + 1 ] != str[ i ] && ( j >= 0 ) )
    {
      j = next[ j ];
    }
    if( str[ i ] == str[ j + 1 ] )
    {
      next[ i ] = j + 1;
    }
    else
    {
      next[ i ] = -1;
    }
  }
}

int KMP( char * str, int slen, char * ptr, int plen, int * next )
{
  int s_i = 0, p_i = 0;

  while( s_i < slen && p_i < plen )
  {
    if( str[ s_i ] == ptr[ p_i ] )
    {
      s_i++;
      p_i++;
    }
    else
    {
      if( p_i == 0 )
      {
        s_i++;
      }
      else
      {
        p_i = next[ p_i - 1 ] + 1;
      }
    }
  }
  return ( p_i == plen ) ? ( s_i - plen ) : -1;
}

int main()
{
  char str[ N ] = {0};
  char ptr[ N ] = {0};
  int slen, plen;
  int next[ N ];

  while( scanf( "%s%s", str, ptr ) )
  {
    slen = strlen( str );
    plen = strlen( ptr );
    cal_next( ptr, next, plen );
    printf( "%d\n", KMP( str, slen, ptr, plen, next ) );
  }
  return 0;
}

老实说还是不明白，接着看这篇博文，大概就理解了

原文地址：http://blog.csdn.net/yutianzuijin/article/details/11954939/

kmp算法又称“看毛片”算法，是一个效率非常高的字符串匹配算法。不过由于其难以理解，所以在很长的一段时间内一直没有搞懂。虽然网上有很多资料，但是鲜见好的博客能简单明了地将其讲清楚。在此，综合网上比较好的几个博客（参见最后），尽自己的努力争取将kmp算法思想和实现讲清楚。

kmp算法完成的任务是：给定两个字符串O和f，长度分别为n和m，判断f是否在O中出现，如果出现则返回出现的位置。常规方法是遍历a的每一个位置，然后从该位置开始和b进行匹配，但是这种方法的复杂度是O(nm)。kmp算法通过一个O(m)的预处理，使匹配的复杂度降为O(n+m)。

kmp算法思想

我们首先用一个图来描述kmp算法的思想。在字符串O中寻找f，当匹配到位置i时两个字符串不相等，这时我们需要将字符串f向前移动。常规方法是每次向前移动一位，但是它没有考虑前i-1位已经比较过这个事实，所以效率不高。事实上，如果我们提前计算某些信息，就有可能一次前移多位。假设我们根据已经获得的信息知道可以前移k位，我们分析移位前后的f有什么特点。我们可以得到如下的结论：

• A段字符串是f的一个前缀。
• B段字符串是f的一个后缀。
• A段字符串和B段字符串相等。

所以前移k位之后，可以继续比较位置i的前提是f的前i-1个位置满足：长度为i-k-1的前缀A和后缀B相同。只有这样，我们才可以前移k位后从新的位置继续比较。

所以kmp算法的核心即是计算字符串f每一个位置之前的字符串的前缀和后缀公共部分的最大长度（不包括字符串本身，否则最大长度始终是字符串本身）。获得f每一个位置的最大公共长度之后，就可以利用该最大公共长度快速和字符串O比较。当每次比较到两个字符串的字符不同时，我们就可以根据最大公共长度将字符串f向前移动(已匹配长度-最大公共长度)位，接着继续比较下一个位置。事实上，字符串f的前移只是概念上的前移，只要我们在比较的时候从最大公共长度之后比较f和O即可达到字符串f前移的目的。

next数组计算

理解了kmp算法的基本原理，下一步就是要获得字符串f每一个位置的最大公共长度。这个最大公共长度在算法导论里面被记为next数组。在这里要注意一点，next数组表示的是长度，下标从1开始；但是在遍历原字符串时，下标还是从0开始。假设我们现在已经求得next[1]、next[2]、……next[i]，分别表示长度为1到i的字符串的前缀和后缀最大公共长度，现在要求next[i+1]。由上图我们可以看到，如果位置i和位置next[i]处的两个字符相同（下标从零开始），则next[i+1]等于next[i]加1。如果两个位置的字符不相同，我们可以将长度为next[i]的字符串继续分割，获得其最大公共长度next[next[i]]，然后再和位置i的字符比较。这是因为长度为next[i]前缀和后缀都可以分割成上部的构造，如果位置next[next[i]]和位置i的字符相同，则next[i+1]就等于next[next[i]]加1。如果不相等，就可以继续分割长度为next[next[i]]的字符串，直到字符串长度为0为止。由此我们可以写出求next数组的代码（java版）：

public int[] getNext(String b)  
{  
    int len=b.length();  
    int j=0;  
          
    int next[]=new int[len+1];//next表示长度为i的字符串前缀和后缀的最长公共部分，从1开始  
    next[0]=next[1]=0;  
          
    for(int i=1;i0&&b.charAt(i)!=b.charAt(j))j=next[j];  
        if(b.charAt(i)==b.charAt(j))j++;  
        next[i+1]=j;  
    }  
          
    return next;  
}  

上述代码需要注意的问题是，我们求取的next数组表示长度为1到m的字符串f前缀的最大公共长度，所以需要多分配一个空间。而在遍历字符串f的时候，还是从下标0开始(位置0和1的next值为0，所以放在循环外面)，到m-1为止。代码的结构和上面的讲解一致，都是利用前面的next值去求下一个next值。

字符串匹配

计算完成next数组之后，我们就可以利用next数组在字符串O中寻找字符串f的出现位置。匹配的代码和求next数组的代码非常相似，因为匹配的过程和求next数组的过程其实是一样的。假设现在字符串f的前i个位置都和从某个位置开始的字符串O匹配，现在比较第i+1个位置。如果第i+1个位置相同，接着比较第i+2个位置；如果第i+1个位置不同，则出现不匹配，我们依旧要将长度为i的字符串分割，获得其最大公共长度next[i]，然后从next[i]继续比较两个字符串。这个过程和求next数组一致，所以可以匹配代码如下（java版）：

public void search(String original, String find, int next[]) {  
    int j = 0;  
    for (int i = 0; i < original.length(); i++) {  
        while (j > 0 && original.charAt(i) != find.charAt(j))  
            j = next[j];  
        if (original.charAt(i) == find.charAt(j))  
            j++;  
        if (j == find.length()) {  
            System.out.println("find at position " + (i - j));  
            System.out.println(original.subSequence(i - j + 1, i + 1));  
            j = next[j];  
        }  
    }  
}  

上述代码需要注意的一点是，每次我们得到一个匹配之后都要对j重新赋值。

复杂度

kmp算法的复杂度是O(n+m)，可以采用均摊分析来解答，具体可参考算法导论。