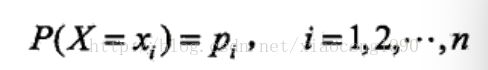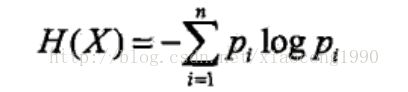分类决策树原理及实现(三)

三、特征选择

   特征选择，即选择来对特征空间进行划分。准则是信息增益（对应ID3算法）或信息增益比(对应C4.5算法)，ID3与C4.5

大部分相同，只是选择特征准则计算公式不同。以ID3为例，从根结点开始，对结点计算所有特征的信息增益，然后选择具

有最大信息增益的特征作为结点的特征，由该特征不同的取值建立相应的子结点；再对递归地对子结点调上以上方法，构建

决策树，直至没见有特征可以选择或所有特征的信息增益很小为止。ID3相当用极大似然法进行概率模型选择。

   为了解释信息增益，先结出熵与条件熵的定义。

   熵表示随机变量不确定性的度量，熵越大，随机变量不确定性越大。

   设X是一个取有限个值的离散随机变量，其概率分布为，

   则X的熵定义为

   

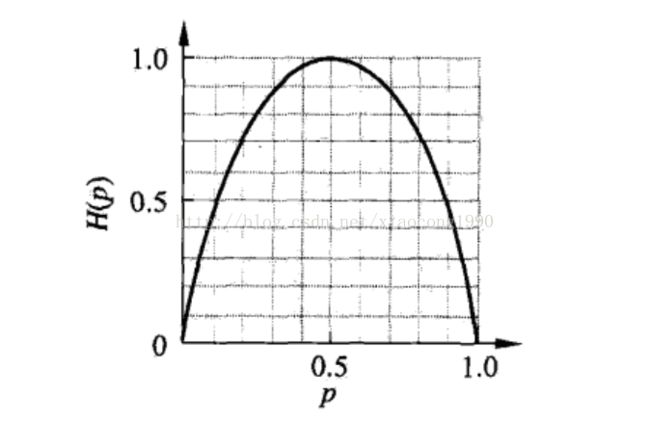
  熵H(p)随概率p变化的曲线如下，

  好了，熵的定义就到这里了。下面讲解信息增益

   特征A对训练集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，

即 g(D,A)=H(D)-H(D|A) ,H(D)表示对数据集D进行分类的不确定性，H(D|A)表示特征A给定条件下对数据集D进行

分类的不确定性。它们的差，即信息增益，就表示由于特征A而使得对数据集D分类的不确定性减少的程度。信息

增益大的特征具有更强的分类能力。

   根据信息增益的特征选择方法，计算每一个特征的信息增益，选择具有最大信息增益的特征对数据进行划分。

    

  

以下是python实现源码，题目原型在 分类决策树(四)

def createDataSet():
    """
    建立数据集
    :return: 数据集,特征标签
    """
    dataSet=[['youth', 'wantJob', 'wantHouse', 'ordinary', 'no'],
             ['youth', 'wantJob', 'wantHouse', 'well', 'no'],
             ['youth', 'hasJob', 'wantHouse', 'well', 'yes'],
             ['youth', 'hasJob', 'hasHouse', 'ordinary', 'yes'],
             ['youth', 'wantJob', 'wantHouse', 'ordinary', 'no'],
             ['midlife', 'wantJob', 'wantHouse', 'ordinary', 'no'],
             ['midlife', 'wantJob', 'wantHouse', 'well', 'no'],
             ['midlife', 'hasJob', 'hasHouse', 'well', 'yes'],
             ['midlife', 'wantJob', 'hasHouse', 'best', 'yes'],
             ['midlife', 'wantJob', 'hasHouse', 'best', 'yes'],
             ['elderly', 'wantJob', 'hasHouse', 'best', 'yes'],
             ['elderly', 'wantJob', 'hasHouse', 'well', 'yes'],
             ['elderly', 'hasJob', 'wantHouse', 'well', 'yes'],
             ['elderly', 'hasJob', 'wantHouse', 'best', 'yes'],
             ['elderly', 'wantJob', 'wantHouse', 'ordinary', 'no'],]
    labels=['age','Job','House','creditLoan']
    return dataSet,labels

def calcCntropy(dataSet):
    """
    计算熵
    :param dataSet:数据集
    :return: 熵
    """
    dataNum=len(dataSet)  #数据集长度
    classCounts={}
    for featVec in dataSet:
        currClass=featVec[-1]
        if currClass not in classCounts.keys():
            classCounts[currClass]=0
        classCounts[currClass]+=1
    cntropy=0.0 #熵
    for value in classCounts.values():
        prob=float(value)/dataNum
        cntropy-=prob*log(prob,2)
    return cntropy

def splitDataSet(dataSet,axis,value):
    """
    根据某一特征划分数据
    :param dataSet: 待划分的数据集
    :param axis: 待划分数据集的特征
    :param value: 特征值
    :return:划分后数据集
    """
    reduceDataSet=[] #剩余的数据
    for featVec in dataSet:
        if featVec[axis]==value:
            reduceFeatVec=featVec[:axis]
            reduceFeatVec.extend(featVec[axis+1:])
            reduceDataSet.append(reduceFeatVec)
    return reduceDataSet


def chooseBestFeatureToSplit(dataSet):
    """
    根据信息增益准则选择待划分特征
    :param dataSet: 待划分数据集
    :return: 待划分特征
    """
    featNum=len(dataSet[0])-1 #特征数
    baseEntropy=calcCntropy(dataSet) #经验熵
    #print baseEntropy
    bestInfoGain=0.0 #最大信息增益
    bestFeature=-1 #最优先划分特征
    for i in range(featNum):

        featList=set([featVec[i] for featVec in dataSet]) #特征值列表
        condEntopy=0.0 #条件熵
        for value in featList:
            subDataSet=splitDataSet(dataSet,i,value)
            prob=float(len(subDataSet))/float(len(dataSet))
            condEntopy+=prob*calcCntropy(subDataSet)
        infoGain=baseEntropy-condEntopy  #信息增益

        if infoGain>bestInfoGain:
            bestInfoGain=infoGain
            bestFeature=i
    return bestFeature

分类决策树（四）

http://blog.csdn.net/xiaocong1990/article/details/54646837