LeetCode 5208. 穿过迷宫的最少移动次数

5208. 穿过迷宫的最少移动次数

可以访问我的博客，嘎嘎

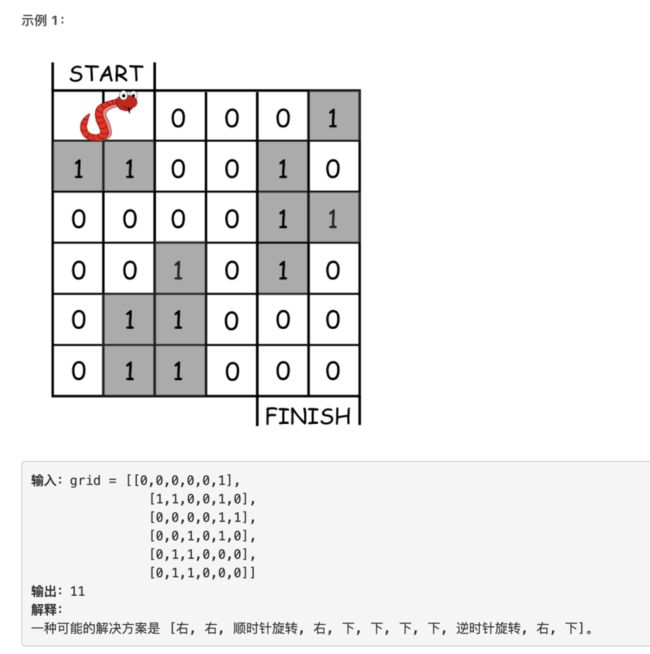
题目描述

思想

想法很简单，就是用BFS一层一层的搜索就可以。但针对这个问题，有些地方需要改变下。

首先是当前位置

以前在一个二维地图上进行BFS，当前位置都是用$(i,j)$这样一个坐标表示的，但现在这条小蛇独占了2个格子，也就是需要用两个坐标来表示，即$(i_1,j_1),(i_2,j_2)$，约定第一个坐标表示蛇的尾部，第二个坐标表示蛇的头部。为了方便实现，我们定义一个结构体：

struct Node {
    int a, b, c, d;
    Node() {}
    Node(int _a, int _b, int _c, int _d) : a(_a), b(_b), c(_c), d(_d) {}
};

其中(a,b)对应着$(i_1,j_1)$，同理，(c,d)对应着$(i_2,j_2)$。

然后是记录已经访问过的“小蛇的位置”

以前都是用visited[i][j]来表示$(i,j)$有没有被访问过，而在这里，我定义了一个集合:

set<Node> visited;

再有就是“如何走”

从某个位置可以走的方案一共四种，分别是：

Node try_right =        Node(p.a, p.b+1, p.c, p.d+1);
Node try_down =       Node(p.a+1, p.b, p.c+1, p.d);
Node try_clockwise = Node(p.a, p.b, p.a+1, p.b);
Node try_anti =         Node(p.a, p.b, p.a, p.b+1);

代码实现

struct Node {
    int a, b, c, d;
    Node() {}
    Node(int _a, int _b, int _c, int _d) : a(_a), b(_b), c(_c), d(_d) {}
    bool operator < (const Node &n) const {
        if (a != n.a) return a < n.a;
        if (b != n.b) return b < n.b;
        if (c != n.c) return c < n.c;
        if (d != n.d) return d < n.d;
        return false;
    }
};

class Solution {
public:
    
    int minimumMoves(vector<vector<int>>& grid) {
        Node start = Node(0, 0, 0, 1);
        set<Node> visited;
        visited.insert(start);
        deque<Node> d;
        d.push_back(start);
        
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        while (!d.empty()) {
            
            int len = d.size();
            for (int i = 0 ; i < len; i++) {
                Node &p = d.front();
                if (p.a == (m-1) && p.c == (m-1) && p.b == (n-2) && p.d == (n-1)) {
                    return ans;
                }

                Node try_right =     Node(p.a, p.b+1, p.c, p.d+1);
                Node try_down =      Node(p.a+1, p.b, p.c+1, p.d);
                Node try_clockwise = Node(p.a, p.b, p.a+1, p.b);
                Node try_anti =      Node(p.a, p.b, p.a, p.b+1);

                if (p.a == p.c) { //小蛇是横着的
                    if (try_right.d < n && grid[try_right.c][try_right.d] != 1 && visited.find(try_right) == visited.end()) {
                        visited.insert(try_right);
                        d.push_back(try_right);
                    }
                    if (try_down.a < m && grid[try_down.a][try_down.b] != 1 && grid[try_down.c][try_down.d] != 1) {
                        if (visited.find(try_down) == visited.end()) {
                            visited.insert(try_down);
                            d.push_back(try_down);  
                        }
                        if (visited.find(try_clockwise) == visited.end()) {
                            visited.insert(try_clockwise);
                            d.push_back(try_clockwise);
                        }
                    }
                }
                else { //小蛇是竖着的
                    if (try_down.c < m && grid[try_down.c][try_down.d] != 1 && visited.find(try_down) == visited.end()) {
                        visited.insert(try_down);
                        d.push_back(try_down);
                    }
                    if (try_right.b < n && grid[try_right.a][try_right.b] != 1 && grid[try_right.c][try_right.d] != 1) {
                        if (visited.find(try_right) == visited.end()) {
                            visited.insert(try_right);
                            d.push_back(try_right);
                        }
                        if (visited.find(try_anti) == visited.end()) {
                            visited.insert(try_anti);
                            d.push_back(try_anti);
                        }
                    }
                }
                d.pop_front();
            }
            ans++;
        }
        
        return -1;
    }
};