洛谷P1081 开车旅行
题目描述
小 A 和小 B 决定利用假期外出旅行,他们将想去的城市从 1 到 N 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i 的海拔高度为Hi,城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值,即d[i,j] = |Hi− Hj|。 旅行过程中,小 A 和小 B 轮流开车,第一天小 A 开车,之后每天轮换一次。他们计划选择一个城市 S 作为起点,一直向东行驶,并且最多行驶 X 公里就结束旅行。小 A 和小 B的驾驶风格不同,小 B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A 总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出 X 公里,他们就会结束旅行。
在启程之前,小 A 想知道两个问题:
对于一个给定的 X=X0,从哪一个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小(如果小 B 的行驶路程为 0,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
- 对任意给定的 X=Xi和出发城市 Si,小 A 开车行驶的路程总数以及小 B 行驶的路程总数。
输入输出格式
输入格式:第一行包含一个整数 N,表示城市的数目。
第二行有 N 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 到城市 N 的海拔高度,即 H1,H2,……,Hn,且每个 Hi都是不同的。
第三行包含一个整数 X0。
第四行为一个整数 M,表示给定 M 组 Si和 Xi。
接下来的 M 行,每行包含 2 个整数 Si和 Xi,表示从城市 Si出发,最多行驶 Xi公里。
输出共 M+1 行。
第一行包含一个整数 S0,表示对于给定的 X0,从编号为 S0的城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小。
接下来的 M 行,每行包含 2 个整数,之间用一个空格隔开,依次表示在给定的 Si和
Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。
输入输出样例
4 2 3 1 4 3 4 1 3 2 3 3 3 4 3
1 1 1 2 0 0 0 0 0
10 4 5 6 1 2 3 7 8 9 10 7 10 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7
2 3 2 2 4 2 1 2 4 5 1 5 1 2 1 2 0 0 0 0 0
说明
【输入输出样例 1 说明】
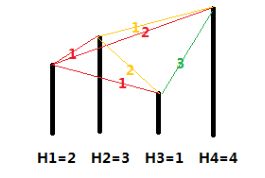
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 1 出发,可以到达的城市为 2,3,4,这几个城市与城市 1 的距离分别为 1,1,2,但是由于城市 3 的海拔高度低于城市 2,所以我们认为城市 3 离城市 1 最近,城市 2 离城市1 第二近,所以小 A 会走到城市 2。到达城市 2 后,前面可以到达的城市为 3,4,这两个城市与城市 2 的距离分别为 2,1,所以城市 4 离城市 2 最近,因此小 B 会走到城市 4。到达城市 4 后,前面已没有可到达的城市,所以旅行结束。
如果从城市 2 出发,可以到达的城市为 3,4,这两个城市与城市 2 的距离分别为 2,1,由于城市 3 离城市 2 第二近,所以小 A 会走到城市 3。到达城市 3 后,前面尚未旅行的城市为4,所以城市 4 离城市 3 最近,但是如果要到达城市 4,则总路程为 2+3=5>3,所以小 B 会直接在城市 3 结束旅行。
如果从城市 3 出发,可以到达的城市为 4,由于没有离城市 3 第二近的城市,因此旅行
还未开始就结束了。
如果从城市 4 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【输入输出样例 2 说明】
当 X=7 时, 如果从城市 1 出发,则路线为 1 -> 2 -> 3 -> 8 -> 9,小 A 走的距离为 1+2=3,小 B 走的距离为 1+1=2。(在城市 1 时,距离小 A 最近的城市是 2 和 6,但是城市 2 的海拔更高,视为与城市 1 第二近的城市,所以小 A 最终选择城市 2;走到 9 后,小 A 只有城市 10 可以走,没有第 2 选择可以选,所以没法做出选择,结束旅行)
如果从城市 2 出发,则路线为 2 -> 6 -> 7 ,小 A 和小 B 走的距离分别为 2,4。
如果从城市 3 出发,则路线为 3 -> 8 -> 9,小 A 和小 B 走的距离分别为 2,1。
如果从城市 4 出发,则路线为 4 -> 6 -> 7,小 A 和小 B 走的距离分别为 2,4。
如果从城市 5 出发,则路线为 5 -> 7 -> 8 ,小 A 和小 B 走的距离分别为 5,1。
如果从城市 6 出发,则路线为 6 -> 8 -> 9,小 A 和小 B 走的距离分别为 5,1。
如果从城市 7 出发,则路线为 7 -> 9 -> 10,小 A 和小 B 走的距离分别为 2,1。
如果从城市 8 出发,则路线为 8 -> 10,小 A 和小 B 走的距离分别为 2,0。
如果从城市 9 出发,则路线为 9,小 A 和小 B 走的距离分别为 0,0(旅行一开始就结
束了)。
如果从城市10出发,则路线为 10,小A 和小B 走的距离分别为0,0。
从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小,但是城市 2 的海拔更高,所以输出第一行为 2。
对于30%的数据,有1≤N≤20,1≤M≤20;
对于40%的数据,有1≤N≤100,1≤M≤100;
对于50%的数据,有1≤N≤100,1≤M≤1,000;
对于70%的数据,有1≤N≤1,000,1≤M≤10,000;
对于100%的数据,有1≤N≤100,000,1≤M≤100,000,-1,000,000,000≤Hi≤1,000,000,000,0≤X0≤1,000,000,000,1≤Si≤N,0≤Xi≤1,000,000,000,数据保证Hi 互不相同。
题解 Here !!!
首先思路是倍增:
令f[I][J]表示以I出发2^J个点所到达的点
令apath[I][J]表示以I出发2^J个点a所行驶的距离
令bpath[I][J]表示以I出发2^J个点b所行驶的距离
首先,你需要找到n个点距离他最近的点与次近的点。
因为只需寻找次近与最近,所以可以先排序,用链表连起来。
然后链表的点也要对应回来,因为我们必须由这个点得到i所对应链表的位置。
然后因为是只有从后面往前面走,那么我们就顺次寻找,找完一个删除一个。
值得注意的是,对于一个点 x ,他的最近的点肯定只可能是相邻的任意一个点。
然后我们暂时删除最近的点,此时次近的点依旧是相邻的点。
另外,因为可能越界,即左右两边没有城市了,那么我们还需要进行两次判断,这里具体见代码。
找完了次近与最近,这时候就可以倍增处理了,倍增处理完了以后,就是一般的倍增问题了。
从高位往低位枚举,然后可以的话就跳。
最后还必须看看a能不能再单独跳一次(就是这里坑了我)。
附代码:
#include
#include
#include
#define MAXN 100010
#define MAX 2147483647
using namespace std;
int n,m;
int head[MAXN],front[MAXN],next[MAXN],first[MAXN],second[MAXN];
int f[MAXN][32],apath[MAXN][32],bpath[MAXN][32];
struct node{
int num,id;
}h[MAXN];
inline int read(){
int date=0,w=1;char c=0;
while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
while(c>='0'&&c<='9'){date=date*10+c-'0';c=getchar();}
return date*w;
}
bool cmp(const node &x,const node &y){
return x.num=0;j--)
if(f[u][j]&&v>=apath[u][j]+bpath[u][j]){
v-=apath[u][j]+bpath[u][j];
sa+=apath[u][j];sb+=bpath[u][j];
u=f[u][j];
}
if(apath[u][0]<=v&&second[u])sa+=apath[u][0];
if(sb==0)t=MAX;
else t=(double)sa*1.00000/sb;
if(th[head[ans]].num)){ans=i;s=t;}
}
printf("%d\n",ans);
}
void work2(){
m=read();
for(int i=1;i<=m;i++){
int sa=0,sb=0,u=read(),v=read();
u=head[u];
for(int j=31;j>=0;j--)
if(f[u][j]&&v>=apath[u][j]+bpath[u][j]){
v-=apath[u][j]+bpath[u][j];
sa+=apath[u][j];sb+=bpath[u][j];
u=f[u][j];
}
if(apath[u][0]<=v&&second[u])sa+=apath[u][0];
printf("%d %d\n",sa,sb);
}
}
int main(){
init();
work1();
work2();
return 0;
}