《C》C语言实现FFT算法

一、什么是FFT？

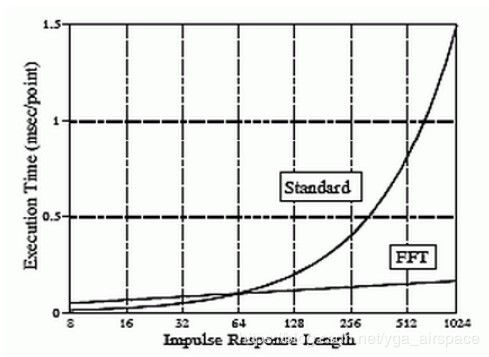
DFT虽好，但是其计算的次数太多，不利于大数据量的计算，FFT是DFT的快速算法，可以节省大量的计算时间，快速傅里叶变换（FFT）是一种能在O(nlogn)的时间内将一个多项式转换成它的点值表示的算法。

• 点值表示法：

  设一个函数f(x)为n-1次多项式，带入一个n个不同的x会得到n个不同的y，这n对(x,y)唯一确定了该多项式，即只有一个多项式能同时满足“代入这些x，得到的分别是这些y”。

二、FFT的目的

FFT可以用来加速多项式乘法。假设有两个n−1次多项式A(x)和B(x)，我们的目标是——把它们乘起来。
普通的多项式乘法的复杂度是O(n2)的，我们要枚举A(x)中的每一项，分别与B(x)中的每一项相乘，来得到一个新的多项式C(x)。
但是，如果A(x)，B(x)两个多项式用点值表示的方法进行相乘，复杂度是O(n)的。具体方法：C(xi)=A(xi)×B(xi)，所以枚举xi即可。
要是我们把两个多项式转换成点值表示，再相乘，再把新的点值表示转换成多项式岂不就可以O(n)的复杂度来解决多项式乘法了！
显然，把多项式转换成点值表示的朴素算法是$O(n^2)$的。难道大整数乘法就只能是$O(n^2)$吗？不甘心的同学可以发现，大整数乘法复杂度的瓶颈可能在“多项式转换成点值表示”这一步做改进，只要完成这一步就可以O(n)的复杂度求答案了。傅里叶变换的发明就是为完成这个使命。

三、FFT过程分析

1. 复数的引入

傅里叶规定点值表示中的n个x为n个模长为1的复数。
而这n个复数不是随机寻找的，而是把单位圆（圆心为原点、1为半径的圆）n等分，取这n个点所表示的复数，即分别以这n个点的横坐标为实部、纵坐标为虚部，所构成的复数。

从点(1,0)开始，逆时针将这n个点从0开始编号，第k个点对应的虚数记作$w_n^k$，根据复数相乘时模长相乘幅角相加可以看出，$w_n^k$是$w_n^1$的k次方，所以$w_n^1$被称为n次单位根。
根据每个复数的幅角，可以计算出所对应的点。$w_n^k$对应的点是$(cos2\pi \frac{k}{n},sin2\pi \frac{k}{n})$，也就是说这个复数是$cos2\pi \frac{k}{n}+isin2\pi \frac{k}{n}$。
把这n个复数${\omega }_n^0,{\omega }_n^1,{\omega }_n^2,...,{\omega }_n^{n-1}$代入多项式，能得到一种特殊的点值表示，这种点值表示就叫离散傅里叶变换

2. 分治的思想

我们要计算n个采样点
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ $$p=p_0，p_1，...，p_{n-1}$$
的傅里叶变换，可以归结为计算多项式
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ $$f(x)=p_0+p_{1}x+p_{2}x+...+p_{n-1}{x}^n-1$$
在各n次单位根$1，w，w^2，...，w^{n-1}$上的值，即
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ $$f_0=p_0+p_1+p_2+...+p_{n-1}$$
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ $$f_1=p_0+p_{1}w+p_2{w}^2+...+p_{n-1}{w}^{n-1}$$
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ $$f_2=p_0+p_1{w}^2+p_2(w^2{)}^2+...+p_{n-1}(w^2{)}^{n-1}$$
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ …
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ $$f_{n-1}=p_0+p_1{w}^{n-1}+p_2(w^{n-1}{)}^2+...+p_{n-1}(w^{n-1}{)}^{n-1}$$
其中
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ $$w=e^{-j\frac{2\pi }{n}}$$
为n次单位元根。
若n是2的k次幂，即$n=2^k$(k>0)，则f(x)可以分解为关于系数下标的奇、偶两部分，即
​ ​ ​ ​ ​ ​ ​ ​ ​ ​$$f(x)=p_0+p_2{x}^2+...+p_{n-2}{x}^{n-2}+x(p_1+p_3{x}^2+...+p_{n-1}{x}^{n-2}$$
若令
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​$$p_{even}(x^2)=p_0+p_2{x}^2+...+p_{n-2}{x}^{n-2}$$
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​$$p_{odd}(x^2)=p_1+p_3{x}^2+...+p_{n-1}{x}^{n-2}$$
则有
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​$$f(x)=p_{even}(x^2)+x{p}_{odd}(x^2)$$
并且有
​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​$$f(-x)=p_{even}(x^2)-x{p}_{odd}(x^2)$$
由此可以看出，为了求f(x)在各n次单位根上的值，只需求$p_{even}(x)和p_{odd}(x)在1，w^2，...，(w^{(n/2)-1}{)}^2$上的值就可以了。
而$p_{even}$和$p_{odd}$同样可以分解成关于$x^2$的偶次幂和奇次幂两部分。依此类推，一直分解下去，最后可归纳为只需求2次单位根$w_2^1$上1和-1的值。
在实际计算中，可以将上述过程倒过来进行，这就是FFT算法。

四、C语言实现FFT

1. 函数语句与形参说明

void kfft (pr，pi，n，k，fr，fi，il)

形参与函数类型	参数意义
double pr[n]	存放n个采样输入的实部，返回离散傅里叶变换的摸
double pi[n]	存放n个采样输入的虚部
double fr[n]	返回离散傅里叶变换的n个实部
double fi[n]	返回离散傅里叶变换的n个虚部
int n	采样点数
int k	满足$n=2^k$
void kfft()	过程

2. FFT源程序【kfft.c】

  #include "math.h"
  void kfft(pr,pi,n,k,fr,fi)
  int n,k;
  double pr[],pi[],fr[],fi[];
  { 
	int it,m,is,i,j,nv,l0;
    double p,q,s,vr,vi,poddr,poddi;
    for (it=0; it<=n-1; it++)  //将pr[0]和pi[0]循环赋值给fr[]和fi[]
    { 
		m=it; 
		is=0;
		for(i=0; i<=k-1; i++)
        { 
			j=m/2; 
			is=2*is+(m-2*j); 
			m=j;
		}
        fr[it]=pr[is]; 
        fi[it]=pi[is];
    }
    pr[0]=1.0; 
    pi[0]=0.0;
    p=6.283185306/(1.0*n);
    pr[1]=cos(p); //将w=e^-j2pi/n用欧拉公式表示
    pi[1]=-sin(p);

    for (i=2; i<=n-1; i++)  //计算pr[]
    { 
		p=pr[i-1]*pr[1]; 
		q=pi[i-1]*pi[1];
		s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]);
		pr[i]=p-q; pi[i]=s-p-q;
    }
    for (it=0; it<=n-2; it=it+2)  
    { 
		vr=fr[it]; 
		vi=fi[it];
		fr[it]=vr+fr[it+1]; 
		fi[it]=vi+fi[it+1];
		fr[it+1]=vr-fr[it+1]; 
		fi[it+1]=vi-fi[it+1];
    }
	m=n/2; 
	nv=2;
    for (l0=k-2; l0>=0; l0--) //蝴蝶操作
    { 
		m=m/2; 
		nv=2*nv;
        for (it=0; it<=(m-1)*nv; it=it+nv)
          for (j=0; j<=(nv/2)-1; j++)
            { 
				p=pr[m*j]*fr[it+j+nv/2];
				q=pi[m*j]*fi[it+j+nv/2];
				s=pr[m*j]+pi[m*j];
				s=s*(fr[it+j+nv/2]+fi[it+j+nv/2]);
				poddr=p-q; 
				poddi=s-p-q;
				fr[it+j+nv/2]=fr[it+j]-poddr;
				fi[it+j+nv/2]=fi[it+j]-poddi;
				fr[it+j]=fr[it+j]+poddr;
				fi[it+j]=fi[it+j]+poddi;
            }
    }
    for (i=0; i<=n-1; i++)
       { 
		  pr[i]=sqrt(fr[i]*fr[i]+fi[i]*fi[i]);  //幅值计算
       }
    return;
  }

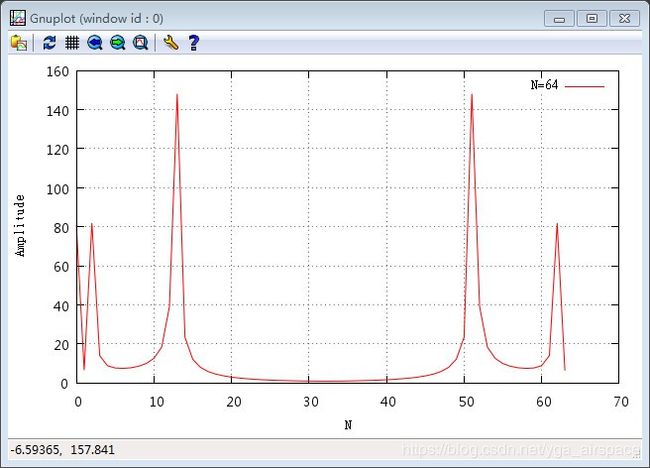
3. 进行傅里叶变换。源程序【FFT.c】

输入信号：$1.2+2.7cos(2\pi \times 33\times t)+5cos(2\pi \times 200\times t+\frac{\pi }{2})$

#include "stdio.h"
#include "math.h"
#include "kfft.c"

#define PI 3.1415926535

main()
{ 
	int i,j;
    double pr[64],pi[64],fr[64],fi[64],t[64];
    for (i=0; i<=63; i++)  //生成输入信号
    { 
		t[i] = i*0.001;
		pr[i]=1.2+2.7*cos(2*PI*33*t[i])+5*cos(2*PI*200*t[i]+PI/2); pi[i]=0.0;
	}
		
    kfft(pr,pi,64,6,fr,fi);  //调用FFT函数
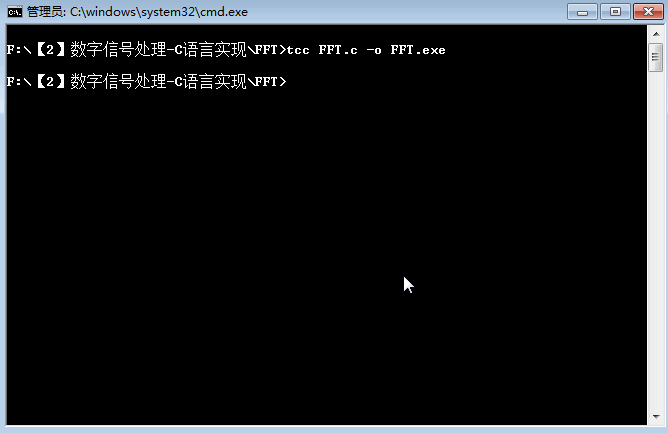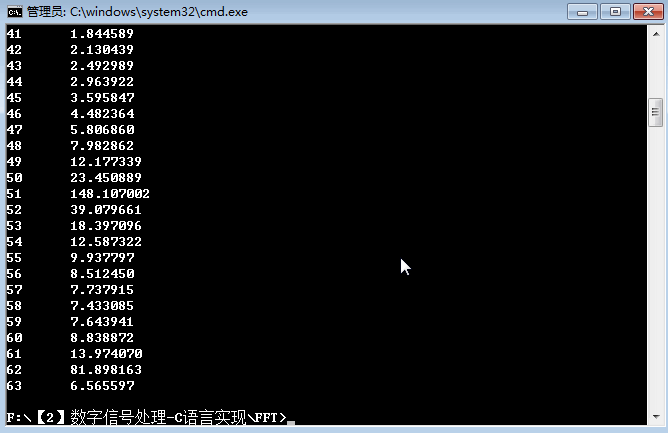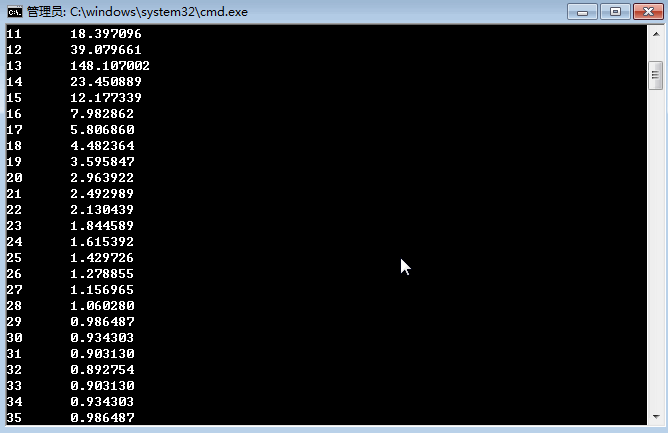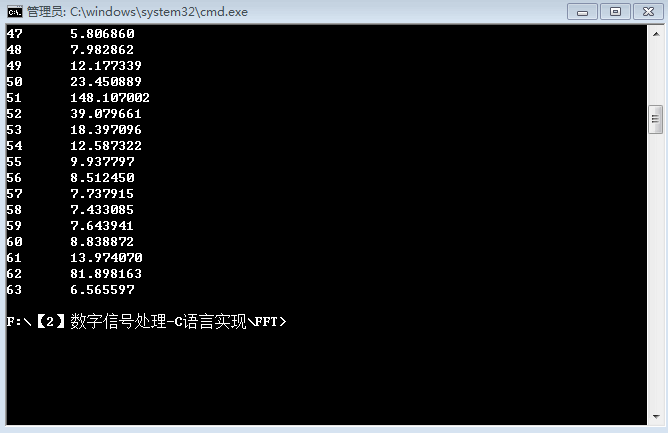
	for (i=0; i<64; i++)
    { 
        printf("%d\t%lf\n",i,pr[i]); //输出结果
    }
}

• 运行结果：
  

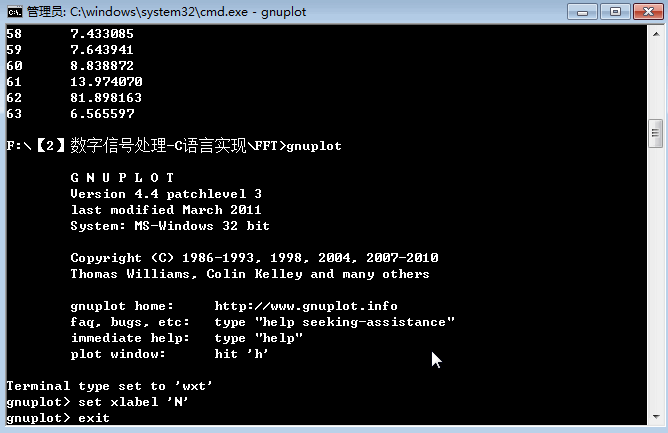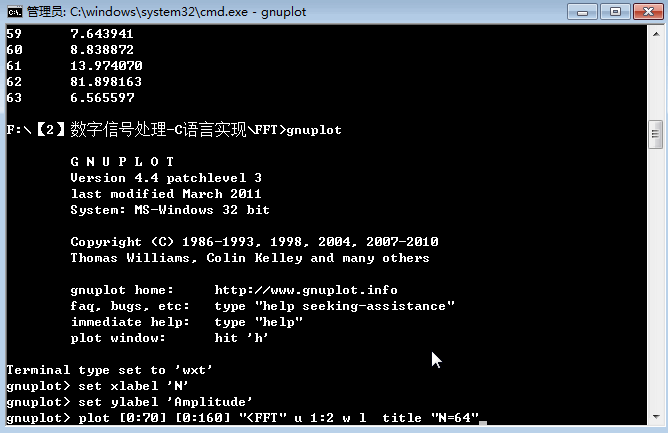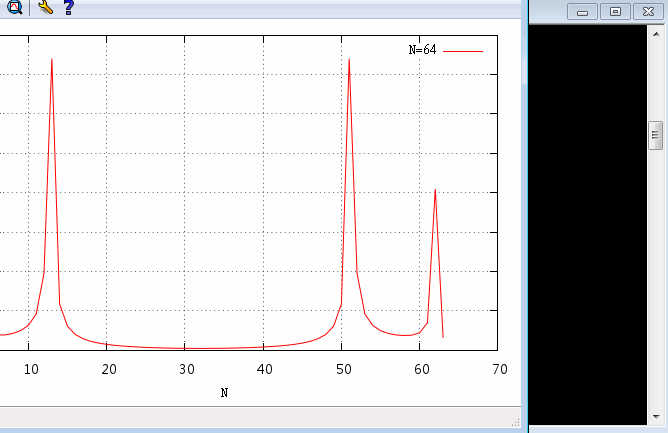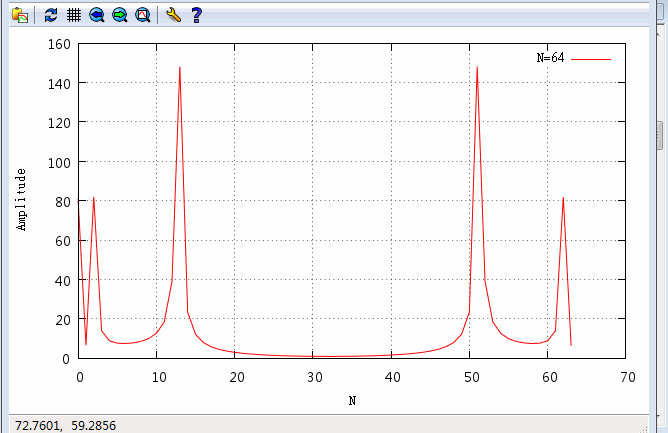
4. 将傅里叶变换的结果，用gnuplot作图

set xlabel "N"
set ylabel "DCT"
plot [0:70] [0:160] "

五、计算结果验证

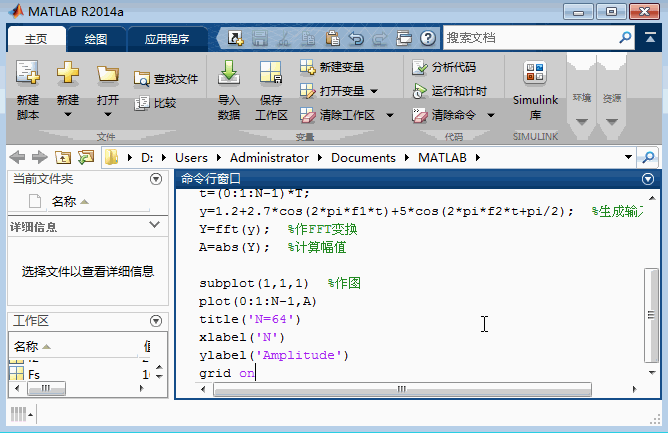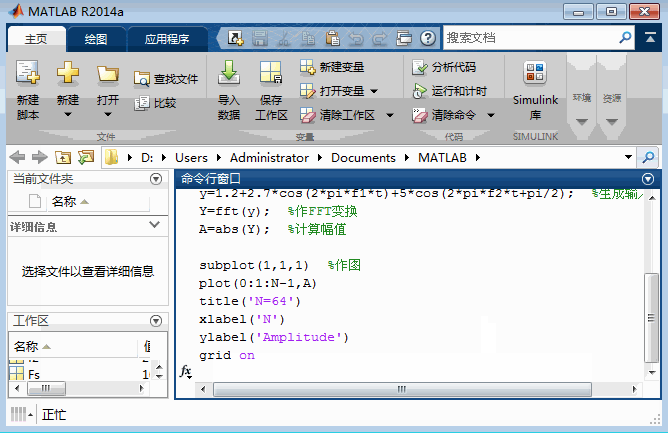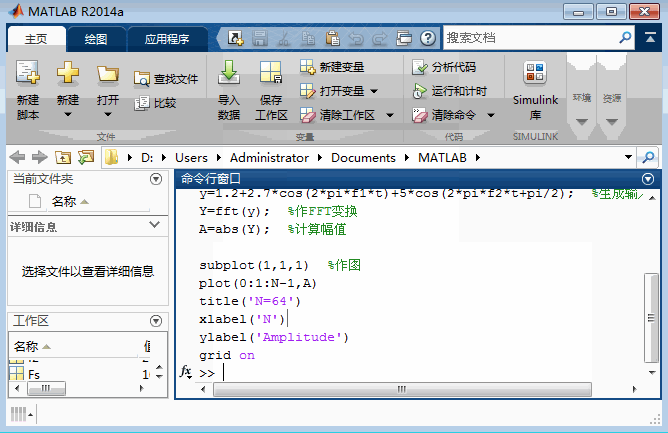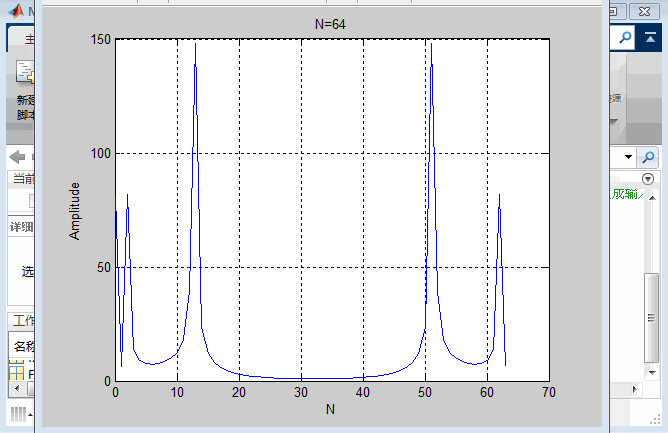
1. matlab实现FFT。源程序【FFT.m】

输入信号：$1.2+2.7cos(2\pi \times 33\times t)+5cos(2\pi \times 200\times t+\frac{\pi }{2})$

Fs=1000;  %采样频率
T=1/Fs;  
N=64;  %序列长度
f1=33; 
f2=200;

t=(0:1:N-1)*T;  
y=1.2+2.7*cos(2*pi*f1*t)+5*cos(2*pi*f2*t+pi/2);  %生成输入信号
Y=fft(y);  %作FFT变换
A=abs(Y);  %计算幅值

subplot(1,1,1)  %作图
plot(0:1:N-1,A)
title('N=64')
xlabel('N')
ylabel('Amplitude')
grid on

• 运行结果：
  

2. 幅值波形图对比

• c语言画图结果：
  
• matlab画图结果：
  

对比两图结果一致