《数据结构与算法分析》二叉堆详解
前言:
博客停止更新了一个星期,因为我回家休假了。本来打算回家一周之内狂学,直接搞定这本书。结果发现家里果然也是时间的黑洞,一天不知道忙啥就结束了,然后加上有小伙伴们诱惑我出去玩,就更加把持不住了。然后彻底弃疗,果断玩了个爽。今天我是来补上拉下的整整一章的博客的。。
我的github:
我实现的代码全部贴在我的github中,欢迎大家去参观。
https://github.com/YinWenAtBIT
介绍:
定义:
二叉堆是一种特殊的堆,二叉堆是完全二元树(二叉树)或者是近似完全二元树(二叉树)。二叉堆有两种:最大堆和最小堆。最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。
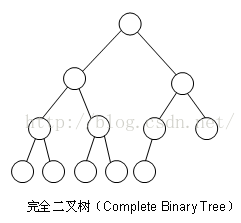
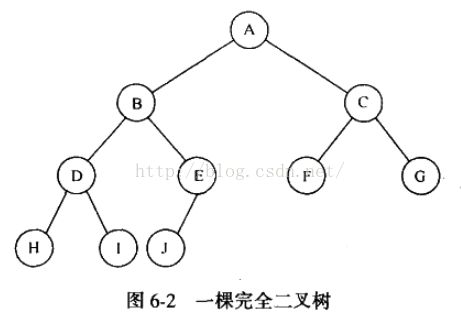
完全二叉树
完全二叉树是一种按照从左到右的顺序,填满每一个深度的树,在第n层深度被填满之前,不会开始填第n+1层深度。如下图所示:
二叉堆有了完全二叉树这个性质,就可以使用数组来实现了,避免了指针之后,就可以直接寻址,大大加快了访问的速度。
这样,我们便可以直接对应上树节点和数组的编号。
注意:在这里数组编号为0的节点不使用,从编号为1的数组开始计数。因为子节点和父亲节点的关系是编号乘以2(+1).为了后续的操作方便,可以在编号为0 的数组节点上储值一个最大值或者最小值。
二叉堆的复杂度
使用二叉堆的主要操作是的插入,与每次提取出最小值(或者最大值)。由于只需要维护父亲节点与子节点之间的大小关系,所以每次插入或者删除,只需要对比操作节点所在的那天线路即可。因此插入和删除的平均运行时间都是O(LogN)。
基本操作:
插入:
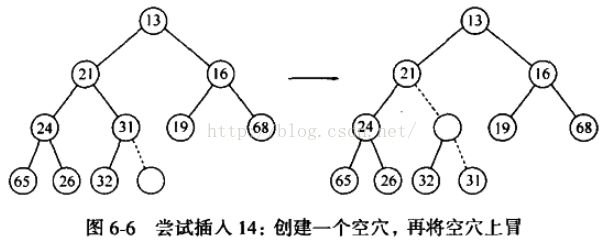
为将一个元素 X 插入到堆中,我们在下一个可用位置创建一个空穴,否则该堆将不是完全数。如果 X 可以放在该空穴中而不破坏堆的序,那么插入完成。否则,我们把空穴的父节点上的元素移入该空穴中,这样,空穴就朝着根的方向上冒一步。继续改过程直到 X 能被放入空穴中为止。
这样一般的策略叫做上滤( percolate up ),指空穴在二叉树中的位置不断上升,直到找的合适的位置;新元素在堆中上滤直到找出正确的位置。
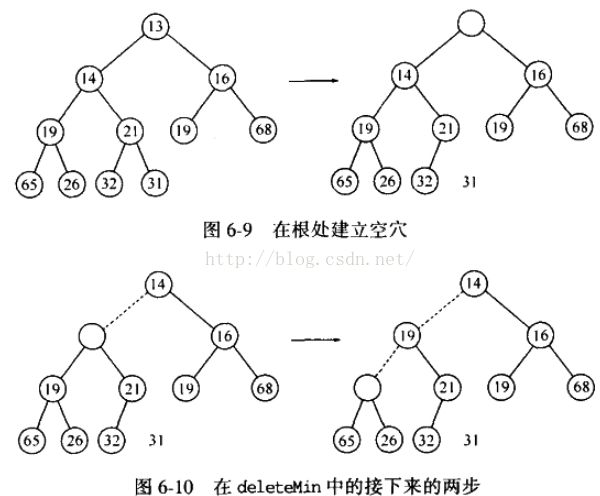
删除最小值/最大值:
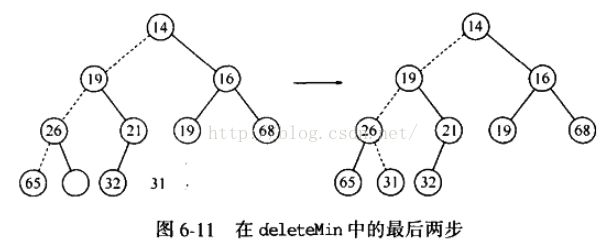
当删除一个最小元时,要在根节点建立一个空穴。由于现在堆少了一个元素,因此堆中最后一个元素 X 必须移动到该堆的某个地方。如果 X 可以直接被放到空穴中,那么 deleteMin 完成。不过这一般不太可能,因此我们将空穴的两个儿子中比较小者移入空穴,这样就把空穴向下推了一层。重复该步骤直到 X 可以被放入空穴中。因此,我们的做法是将 X 置入沿着从根开始包含最小儿子的一条路径上的一个正确的位置。
这种一般的策略叫做下滤(percolate down)。
编码实现:
二叉堆定义:
二叉堆中需要维护一个数组,并且保存已经使用的数组大小和数组容量。
#ifndef _BINARY_HEAP
#define _BINARY_HEAP
struct HeapStruct;
typedef HeapStruct * PriorityQueue;
typedef int ElementType;
PriorityQueue Initialize(int MaxElements);
void Destory(PriorityQueue H);
void makeEmpty(PriorityQueue H);
void Insert(ElementType X, PriorityQueue H);
ElementType DeleteMin(PriorityQueue H);
ElementType FindMin(PriorityQueue H);
int isEmpty(PriorityQueue H);
int isFull(PriorityQueue H);
/*打印二叉堆,利用递归打印,输出结果与二叉树相似*/
void printBHeap(PriorityQueue H, int depth, int Index);
#endif
struct HeapStruct
{
int capacity;
int size;
ElementType * Elements;
};二叉堆初始化:
PriorityQueue Initialize(int MaxElements)
{
PriorityQueue H;
if(MaxElements < 10)
{
fprintf(stderr,"too small elements\n");
return NULL;
}
H = (PriorityQueue)malloc(sizeof(HeapStruct));
if(H ==NULL)
{
fprintf(stderr,"out of space\n");
return NULL;
}
H->capacity = MaxElements;
H->size = 0;
H->Elements = (ElementType *)malloc((MaxElements +1) *sizeof(ElementType));
if(H ->Elements ==NULL)
{
fprintf(stderr,"out of space\n");
return NULL;
}
H->Elements[0] = 0x80000000;
return H;
}插入:
void Insert(ElementType X, PriorityQueue H)
{
if(isFull(H))
return;
int i;
i= ++ H->size ;
while(H->Elements[i/2] > X)
{
H->Elements[i] = H->Elements[i/2];
i = i/2;
}
H->Elements[i] = X;
}删除最小值:
ElementType DeleteMin(PriorityQueue H)
{
if(isEmpty(H))
{
fprintf(stderr,"Queue is empty\n");
return H->Elements[0];
}
ElementType min = H->Elements[1];
ElementType last = H->Elements[H->size--];
if(H->size == 0)
{
return min;
}
int i, child;
for(i=1;;i = child)
{
/*书上的代码没有检查当size=1或者0的情况,这里先检查size是否为1*/
if(2*i > H->size)
break;
child = 2*i;
/*找到左右孩子中最小的一个,如果只有左孩子,就不会比较第二个选项*/
if( child !=H->size && H->Elements[child]>H->Elements[child+1] )
child++;
/*最后一个元素和较小的孩子比较,小的放在空穴中*/
if(last < H->Elements[child])
break;
H->Elements[i] = H->Elements[child];
}
H->Elements[i] = last;
return min;
}测试截图:
第一个输入代表我设置在数组0上的最小值,第二行的15个数字是依次删除15次最小值得到的输出,最后是输入了余下的二叉堆。
总结:
在实现二叉堆的时候,感觉可以化简程序,特别是在插入与删除操作的时候,可以提取出percolate down 和 percolate up操作,这样在buildheap代码编写的时候以及DecreaseKey和IncreaseKey操作时都可以简化编码。不过最后做的时候偷懒没做了。