机器学习(8): 逻辑回归算法 小结及实验
文章目录
- 1 逻辑回归算法简介
- 2 算法原理
- 2.1 线性回归
- 2.2 逻辑回归
- 2.3 损失函数(cost function)
- 2.4 梯度下降法
- (1) 直观理解
- (2) 梯度下降法——代数法
- (3) 梯度下降的种类
- 2.5 线性回归与逻辑回归的区别
- 3 实验
- 3.1 逻辑回归——批量梯度下降法(BGD)
- 3.2 逻辑回归——随机梯度下降法(SGD)
- 3.3 从疝气病症预测病马的死亡率
- 4 逻辑回归算法的优缺点
- 参考资料
注:转载请标明原文出处链接:https://xiongyiming.blog.csdn.net/article/details/97038233
1 逻辑回归算法简介
逻辑回归(Logistic Regression),虽然它的名字中带有“回归”两个字,但是它最擅长处理的却是分类问题。逻辑回归,它是一种很常见的用来解决二元分类问题的方法,它主要是通过寻找最优参数来正确地分类原始数据。逻辑回归分类器适用于各项广义上的分类任务,例如:评论信息的正负情感分析(二分类)、用户点击率(二分类)、用户违约信息预测(二分类)、垃圾邮件检测(二分类)、疾病预测(二分类)、用户等级分类(多分类)等场景。
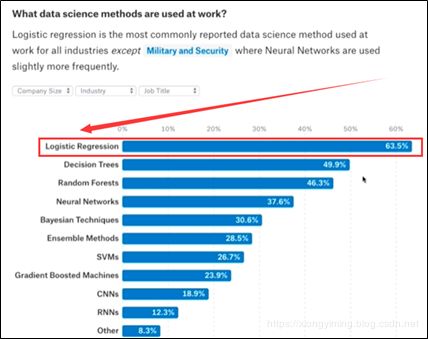
下图是2017年某竞赛网站统计所用到的机器学习算法,其中逻辑回归排名第一。这个数据不能完全说明逻辑回归是非常好的,而近些年深度学习算法不好。经典的算法对数据集以及计算能力要求没有深度学习那么高。所以我么需要根据社用的场景来选择合适的算法,并没有一种算法完全比另一种算法更好。
2 算法原理
2.1 线性回归
提到逻辑回归我们先回顾一下线性回归。
线性回归就是给定一些数据,求得的线性函数尽量的包含所有数据。其表达式为
(1) f ( x ) = w T x + b f({\bf{x}}) = {{\bf{w}}^{\rm{T}}}{\bf{x}} + b \tag{1} f(x)=wTx+b(1)
其中, w {\bf{w}} w和 b b b都是通过学习得到的,最常用的方法就是最小二乘法。
下面举一个一元线性回归的例子。给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } = { ( x i , y i ) } i = 1 m D = \left\{ {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right), \ldots ,\left( {{x_m},{y_m}} \right)} \right\} = \left\{ {\left( {{x_i},{y_i}} \right)} \right\}_{i = 1}^m D={(x1,y1),(x2,y2),…,(xm,ym)}={(xi,yi)}i=1m
而线性回归视图学得:
(2) f ( x i ) = w T x i + b f({x_i}) = {w^{\rm{T}}}{x_i} + b \tag{2} f(xi)=wTxi+b(2)
使得 f ( x i ) ≈ y i f({x_i}) \approx {y_i} f(xi)≈yi。
显然,衡量使用均方误差来衡量 f ( x i ) f({x_i}) f(xi)与 y i {y_i} yi的差距。因此我们任务是将差距最小问题转化为均方误差最小化,即:
(3) ( w ∗ , b ∗ ) = arg min ( w , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2 = arg min ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 \left( {{w^*},{b^*}} \right) = \mathop {\arg \min }\limits_{\left( {w,b} \right)} \sum\limits_{i = 1}^m {{{(f({x_i}) - {y_i})}^2}} = \mathop {\arg \min }\limits_{\left( {w,b} \right)} \sum\limits_{i = 1}^m {{{({y_i} - w{x_i} - b)}^2}} \tag{3} (w∗,b∗)=(w,b)argmini=1∑m(f(xi)−yi)2=(w,b)argmini=1∑m(yi−wxi−b)2(3) 其中, w ∗ , b ∗ {w^*},{b^*} w∗,b∗分别表示 w , b w,b w,b的最优解。
在线性回归中,最小二乘法就是试图找到一条直线,使得所有样本到直线上的欧氏距离之和最小。我们只需要将函数 E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 {E_{(w,b)}} = \sum\limits_{i = 1}^m {{{({y_i} - w{x_i} - b)}^2}} E(w,b)=i=1∑m(yi−wxi−b)2 求导并令导数为0即可求解出 w , b w,b w,b的最优解
(4) w = ∑ i = 1 m y i ( x i − x ˉ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 w = {{\sum\limits_{i = 1}^m {{y_i}({x_i} - \bar x)} } \over {\sum\limits_{i = 1}^m {x_i^2 - {1 \over m}{{\left( {\sum\limits_{i = 1}^m {{x_i}} } \right)}^2}} }} \tag{4} w=i=1∑mxi2−m1(i=1∑mxi)2i=1∑myi(xi−xˉ)(4)
(5) b = 1 m ∑ i = 1 m ( y i − w x i ) b = {1 \over m}\sum\limits_{i = 1}^m {({y_i} - w{x_i})} \tag{5} b=m1i=1∑m(yi−wxi)(5)
2.2 逻辑回归
逻辑回归就是将样本的特征可样本发生的概率联合起来,概率就是一个数,所以就是解决分类问题,一般解决二分类问题。
对于线性回归中, f ( x ) = w T x + b f(x) = {w^{\rm{T}}}x + b f(x)=wTx+b ,这里 f ( x ) f(x) f(x)的范围为 [ − ∞ , + ∞ ] \left[ { - \infty , + \infty } \right] [−∞,+∞],说明通过线性回归中我们可以求得任意的一个值。对于逻辑回归来说就是概率,这个概率取值需要在区间[0,1]内,所以我们将线性回归进行修改:
(6) p = σ ( w T x + b ) p = \sigma \left( {{w^{\rm{T}}}x + b} \right) \tag{6} p=σ(wTx+b)(6)此时,我们希望概率 p p p的取值仅在区间[0,1]内。通常我们使用Sigmoid函数表示 。
对于Sigmoid函数其表达式为
(7) σ ( t ) = 1 1 + e − t \sigma \left( t \right) = {1 \over {1 + {e^{ - t}}}} \tag{7} σ(t)=1+e−t1(7) Sigmoid函数如下图所示:
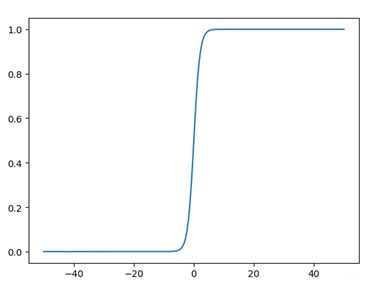
下面是绘制Sigmoid函数的代码
# 绘制Sigmoid函数
import numpy as np
import math
import matplotlib.pyplot as plt
X = np.linspace(-50,50,200)
Y = [1/(1+math.e**(-x)) for x in X]
plt.plot(X,Y)
plt.show()
由公式(7)可以看出,
0.5 < σ ( t ) > 1 , i f t > 0 0.5 < \sigma \left( t \right) > 1,{\rm{ if }}t{\rm{ > 0 }} 0.5<σ(t)>1,ift>0 0 < σ ( t ) < 0.5 , i f t < 0 0 < \sigma \left( t \right) < 0.5,{\rm{ if }}t{\rm{ < 0 }} 0<σ(t)<0.5,ift<0
我们将线性回归问题转化为:
(8) p = σ ( w T x + b ) = 1 1 + e − w T x + b p = \sigma \left( {{w^{\rm{T}}}x + b} \right) = {1 \over {1 + {e^{ - {w^{\rm{T}}}x + b}}}} \tag{8} p=σ(wTx+b)=1+e−wTx+b1(8)
则
(9) f = { 1 , p ≥ 0.5 0 , p < 0.5 f=\left\{\begin{array}{ll}{1,} & {p \geq 0.5} \\ {0,} & {p<0.5}\end{array}\right. \tag{9} f={1,0,p≥0.5p<0.5(9) 那么问题来了,我们在给定样本集我们如何找到最优的参数 w , b w,b w,b?
在逻辑回归问题下比线性回归问题要稍微复杂一些。下面将介绍如何进行求解。
2.3 损失函数(cost function)
对于逻辑回归解决的是二分类问题,因此我们的损失函数也分成两类。对于错误分类的样本,我们对其惩罚越大,则损失函数的值越大,正确分类的样本对其惩罚越小。故对于损失函数来说,我们希望

因此逻辑回归的损失函数可定义为
(10) cost = { − log ( p ^ ) , if y = 1 − log ( 1 − p ^ ) , if y = 0 \operatorname{cost}=\left\{\begin{array}{cc}{-\log (\hat{p}),} & {\text { if } y=1} \\ {-\log (1-\hat{p}),} & {\text { if } y=0}\end{array}\right. \tag{10} cost={−log(p^),−log(1−p^), if y=1 if y=0(10)
其函数图像如下图所示
为了方便计算,我们将这两个损失函数结合起来
(11) c o s t = − y log ( p ^ ) − ( 1 − y ) log ( 1 − p ^ ) {\rm{cost}} = - y\log (\hat p) - (1 - y)\log (1 - \hat p) \tag{11} cost=−ylog(p^)−(1−y)log(1−p^)(11)对于一个样本,我们可以计算损失函数,如公式(11)所示,那么对于样本集所有数据,我们将所有的损失函数加起来得到
(12) J ( w ) = − 1 m ∑ i = 1 m y i log ( p ^ i ) + ( 1 − y i ) log ( 1 − p ^ i ) J(w) = - {1 \over m}\sum\limits_{i = 1}^m {{y_i}} \log ({\hat p_i}) + (1 - {y_i})\log (1 - {\hat p_i}) \tag{12} J(w)=−m1i=1∑myilog(p^i)+(1−yi)log(1−p^i)(12)
其中,
(13) p ^ i = 1 1 + e − w T x + b {\hat p_i} = {1 \over {1 + {e^{ - {w^{\rm{T}}}x + b}}}} \tag{13} p^i=1+e−wTx+b1(13) 为了方便计算,重新定义
(14) p ^ i = 1 1 + e − w T x b {\hat p_i} = {1 \over {1 + {e^{ - {w^{\rm{T}}}{x^b}}}}} \tag{14} p^i=1+e−wTxb1(14)
因此公式(12)可以转化为
(15) J ( w ) = − 1 m ∑ i = 1 m y i log ( σ ( w x i b ) ) + ( 1 − y i ) log ( 1 − σ ( w x i b ) ) J(w) = - {1 \over m}\sum\limits_{i = 1}^m {{y_i}} \log (\sigma (wx_i^b)) + (1 - {y_i})\log (1 - \sigma (wx_i^b)) \tag{15} J(w)=−m1i=1∑myilog(σ(wxib))+(1−yi)log(1−σ(wxib))(15)那么,对于逻辑回归问题,我们的任务就是找到最佳的 w , b w,b w,b,使得损失函数 J ( w ) J(w) J(w)最小这里不能像线性回归那样使用最小二乘法,需要使用梯度下降法来进行求解。
2.4 梯度下降法
(1) 直观理解
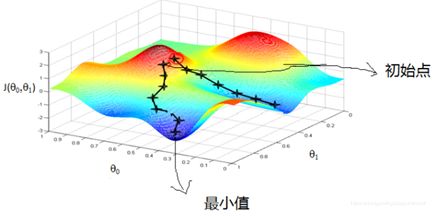
首先来看看梯度下降的一个直观的解释。如下图所示,比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
梯度下降法的算法可以有代数法和向量法两种表示类型的方法。这里详细描述代数法。
前面提到的是根据线性回归一步步引入到逻辑回归,为了和吴恩达老师的机器学习符号保持一致,我们将更改之前用到的符号。
参见之前的博客 https://blog.csdn.net/zaishuiyifangxym/article/details/82110418
(2) 梯度下降法——代数法
假设函数用 h θ ( x 0 , x 1 , … , x n ) = θ 0 + θ 1 x 1 + … + θ n x n {h_\theta }\left( {{x_0},{x_1}, \ldots ,{x_n}} \right) = {\theta _0} + {\theta _1}{x_1} + \ldots + {\theta _n}{x_n} hθ(x0,x1,…,xn)=θ0+θ1x1+…+θnxn表示,其中 θ i ( i = 0 , 1 , … , n ) {\theta _i}\left( {i = 0,1, \ldots ,n} \right) θi(i=0,1,…,n)为模型参数, x i ( i = 0 , 1 , … , n ) {x_i}\left( {i = 0,1, \ldots ,n} \right) xi(i=0,1,…,n) 为样本的特征值。则梯度下降法的算法流程为
算法流程
- 确定当前位置的损失函数的梯度,对于 θ i {\theta _i} θi,其梯度表达式为
∂ ∂ θ i J ( θ i , θ 2 , … , θ n ) {\partial \over {\partial {\theta _i}}}J\left( {{\theta _i},{\theta _2}, \ldots ,{\theta _n}} \right) ∂θi∂J(θi,θ2,…,θn)- 用步长 α \alpha α乘损失函数的梯度,得到当前位置下降的距离,即为
α ∂ ∂ θ i J ( θ i , θ 2 , … , θ n ) \alpha {\partial \over {\partial {\theta _i}}}J\left( {{\theta _i},{\theta _2}, \ldots ,{\theta _n}} \right) α∂θi∂J(θi,θ2,…,θn)这里的步长可以想象前面提到登山例子中的某一步的步长。- 确定是否所有的参数 θ i {\theta _i} θi梯度下降的距离都小于参数 ε \varepsilon ε,则算法终止,当前所有的 θ i ( i = 0 , 1 , … , n ) {\theta _i}\left( {i = 0,1, \ldots ,n} \right) θi(i=0,1,…,n)即为结果(最优值)。否则进入步骤4。
- 更新所有的参数,对于更新的表达式为
θ i = θ i − α ∂ ∂ θ i J ( θ i , θ 2 , … , θ n ) {\theta _i} = {\theta _i} - \alpha {\partial \over {\partial {\theta _i}}}J\left( {{\theta _i},{\theta _2}, \ldots ,{\theta _n}} \right) θi=θi−α∂θi∂J(θi,θ2,…,θn)更新完毕后,转入步骤1。
(3) 梯度下降的种类
- 批量梯度下降法 (Batch Gradient Descent, BGD)
- 随机梯度下降法 (Stochastic Batch Gradient Descent, SGD)
- 小批量梯度下降法 (Mini-Batch Gradient Descent, MBGD)
关于这三种梯度下降法的描述参见博客:https://www.cnblogs.com/lliuye/p/9451903.html
2.5 线性回归与逻辑回归的区别
总的来说,在机器学习中,最小二乘法只适用于线性模型(这里一般指线性回归);而梯度下降适用性极强,一般而言,只要是凸函数,都可以通过梯度下降法得到全局最优值(对于非凸函数,能够得到局部最优解)。梯度下降法只要保证目标函数存在一阶连续偏导,就可以使用
详细的描述见博客:https://blog.csdn.net/zaishuiyifangxym/article/details/93787233
3 实验
3.1 逻辑回归——批量梯度下降法(BGD)
机器学习实战书中的testSet文本文件中的数据集一共有100个点,每个点包含两个数值型特征:X1和X2。因此可以将数据在一个二维平面上展示出来。我们可以将第一列数据(X1)看作x轴上的值,第二列数据(X2)看作y轴上的值。而最后一列数据即为分类标签。根据标签的不同,对这些点进行分类。在此数据集上,我们将通过批量梯度下降法找到最优参数。
伪代码
- 每个回归系数初始化为1
- 重复下面步骤直至收敛:
计算整个数据集的梯度
使用 alpha × gradient 更新回归系数的向量- 返回回归系数
代码示例
import pandas as pd
import numpy as np
# 1 导入数据集
dataSet = pd.read_table('testSet.txt',header = None)
dataSet.columns =['X1','X2','labels']
# print("dataSet=",dataSet)
# 2 定义Sigmoid函数
"""
函数功能:计算sigmoid函数值
参数说明:
inX:数值型数据
返回:
s:经过sigmoid函数计算后的函数值
"""
def sigmoid(inX):
s = 1/(1+np.exp(-inX))
return s
# 2 定义归一化函数
"""
函数功能:归一化(期望为0,方差为1)
参数说明:
xMat:特征矩阵
返回:
inMat:归一化之后的特征矩阵
"""
def regularize(xMat):
inMat = xMat.copy()
inMeans = np.mean(inMat,axis = 0)
inVar = np.std(inMat,axis = 0)
inMat = (inMat - inMeans)/inVar
return inMat
# 3 使用批量梯度下降法
"""
函数功能:使用BGD求解逻辑回归
参数说明:
dataSet:DF数据集
alpha:步长
maxCycles:最大迭代次数
返回:
weights:各特征权重值
"""
def BGD_LR(dataSet,alpha=0.001,maxCycles=500):
xMat = np.mat(dataSet.iloc[:,:-1].values)
yMat = np.mat(dataSet.iloc[:,-1].values).T
xMat = regularize(xMat)
m,n = xMat.shape
weights = np.zeros((n,1))
for i in range(maxCycles):
grad = xMat.T*(xMat * weights-yMat)/m
weights = weights -alpha*grad
return weights
# 4 准确率计算
ws=BGD_LR(dataSet,alpha=0.01,maxCycles=500)
xMat = np.mat(dataSet.iloc[:, :-1].values)
yMat = np.mat(dataSet.iloc[:, -1].values).T
xMat = regularize(xMat)
(xMat * ws).A.flatten()
p = sigmoid(xMat * ws).A.flatten()
for i, j in enumerate(p):
if j < 0.5:
p[i] = 0
else:
p[i] = 1
train_error = (np.fabs(yMat.A.flatten() - p)).sum()
train_error_rate = train_error / yMat.shape[0]
trainAcc = 1-train_error_rate
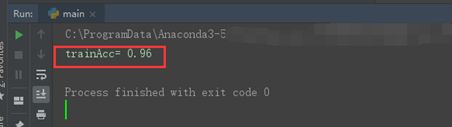
print("trainAcc=",trainAcc)
运行结果
3.2 逻辑回归——随机梯度下降法(SGD)
与上面用到的数据集相同,使用testSet文本文件中的数据集。在此数据集上,我们将通过随机梯度下降法找到最优参数。
代码示例
import pandas as pd
import numpy as np
# 1 导入数据集
dataSet = pd.read_table('testSet.txt',header = None)
dataSet.columns =['X1','X2','labels']
# print("dataSet=",dataSet)
# 2 定义Sigmoid函数
"""
函数功能:计算sigmoid函数值
参数说明:
inX:数值型数据
返回:
s:经过sigmoid函数计算后的函数值
"""
def sigmoid(inX):
s = 1/(1+np.exp(-inX))
return s
# 2 定义归一化函数
"""
函数功能:归一化(期望为0,方差为1)
参数说明:
xMat:特征矩阵
返回:
inMat:归一化之后的特征矩阵
"""
def regularize(xMat):
inMat = xMat.copy()
inMeans = np.mean(inMat,axis = 0)
inVar = np.std(inMat,axis = 0)
inMat = (inMat - inMeans)/inVar
return inMat
# 3 使用随机梯度下降法
"""
函数功能:使用SGD求解逻辑回归
参数说明:
dataSet:DF数据集
alpha:步长
maxCycles:最大迭代次数
返回:
weights:各特征权重值
"""
def SGD_LR(dataSet,alpha=0.001,maxCycles=500):
dataSet = dataSet.sample(maxCycles, replace=True)
dataSet.index = range(dataSet.shape[0])
xMat = np.mat(dataSet.iloc[:, :-1].values)
yMat = np.mat(dataSet.iloc[:, -1].values).T
xMat = regularize(xMat)
m, n = xMat.shape
weights = np.zeros((n,1))
for i in range(m):
grad = xMat[i].T * (xMat[i] * weights - yMat[i])
weights = weights - alpha * grad
return weights
# 4 准确率计算
ws=SGD_LR(dataSet,alpha=0.01,maxCycles=5000)
xMat = np.mat(dataSet.iloc[:, :-1].values)
yMat = np.mat(dataSet.iloc[:, -1].values).T
xMat = regularize(xMat)
(xMat * ws).A.flatten()
p = sigmoid(xMat * ws).A.flatten()
for i, j in enumerate(p):
if j < 0.5:
p[i] = 0
else:
p[i] = 1
train_error = (np.fabs(yMat.A.flatten() - p)).sum()
train_error_rate = train_error / yMat.shape[0]
trainAcc = 1-train_error_rate
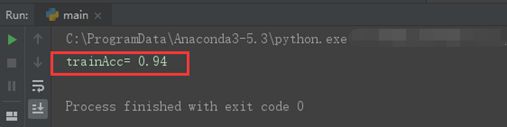
print("trainAcc=",trainAcc)
运行结果
3.3 从疝气病症预测病马的死亡率
将使用Logistic回归来预测患疝气病的马的存活问题。使用机器学习实战书本里的数据。这里的数据包含了368个样本和28个特征。这种病不一定源自马的肠胃问题,其他问题也可能引发马疝病。该数据集中包含了医院检测马疝病的一些指标,有的指标比较主观,有的指标难以测量,例如马的疼痛级别。另外需要说明的是,除了部分指标主观和难以测量外,该数据还存在一个问题,数据集中有30%的值是缺失的。下面将首先介绍如何处理数据集中的数据缺失问题,然后再利用逻辑回归和随机梯度下降法来预测病马的生死。
处理数据
数据中的缺失值是一个非常棘手的问题,很多文献都致力于解决这个问题。那么,数据缺失究竟带来了什么问题?假设有100个样本和20个特征,这些数据都是机器收集回来的。若机器上的某个传感器损坏导致一个特征无效时该怎么办?它们是否还可用?答案是肯定的。因为有时候数据相当昂贵,扔掉和重新获取都是不可取的,所以必须采用一些方法来解决这个问题。下面给出了一些可选的做法:
- 使用可用特征的均值来填补缺失值;
- 使用特殊值来填补缺失值,如-1;
- 忽略有缺失值的样本;
- 使用相似样本的均值添补缺失值;
- 使用另外的机器学习算法预测缺失值。
如果测试集中一条数据的特征值已经确实,那么我们选择实数0来替换所有缺失值,因为我们使用Logistic回归。因此这样做不会影响回归系数的值。sigmoid(0)=0.5,即它对结果的预测不具有任何倾向性。
所以原始的数据集经过处理,保存为两个文件:horseColicTest.txt和horseColicTraining.txt
代码示例
import pandas as pd
import numpy as np
# 1 定义Sigmoid函数
"""
函数功能:计算sigmoid函数值
参数说明:
inX:数值型数据
返回:
s:经过sigmoid函数计算后的函数值
"""
def sigmoid(inX):
s = 1/(1+np.exp(-inX))
return s
# 2 定义归一化函数
"""
函数功能:归一化(期望为0,方差为1)
参数说明:
xMat:特征矩阵
返回:
inMat:归一化之后的特征矩阵
"""
def regularize(xMat):
inMat = xMat.copy()
inMeans = np.mean(inMat,axis = 0)
inVar = np.std(inMat,axis = 0)
inMat = (inMat - inMeans)/inVar
return inMat
# 3 使用随机梯度下降法
"""
函数功能:使用SGD求解逻辑回归
参数说明:
dataSet:DF数据集
alpha:步长
maxCycles:最大迭代次数
返回:
weights:各特征权重值
"""
def SGD_LR(dataSet,alpha=0.001,maxCycles=500):
dataSet = dataSet.sample(maxCycles, replace=True)
dataSet.index = range(dataSet.shape[0])
xMat = np.mat(dataSet.iloc[:, :-1].values)
yMat = np.mat(dataSet.iloc[:, -1].values).T
xMat = regularize(xMat)
m, n = xMat.shape
weights = np.zeros((n,1))
for i in range(m):
grad = xMat[i].T * (xMat[i] * weights - yMat[i])
weights = weights - alpha * grad
return weights
# 4 logistic回归分类函数
"""
函数功能:给定测试数据和权重,返回标签类别
参数说明:
inX:测试数据
weights:特征权重
"""
def classify(inX,weights):
p = sigmoid(sum(inX * weights))
if p < 0.5:
return 0
else:
return 1
# 5 构建logistic模型
"""
函数功能:logistic分类模型
参数说明:
train:测试集
test:训练集
alpha:步长
maxCycles:最大迭代次数
返回:
retest:预测好标签的测试集
"""
def get_acc(train,test,alpha=0.001, maxCycles=5000):
weights = SGD_LR(train,alpha=alpha,maxCycles=maxCycles) # 使用随机梯度下降法
xMat = np.mat(test.iloc[:, :-1].values)
xMat = regularize(xMat)
result = []
for inX in xMat:
label = classify(inX,weights)
result.append(label)
retest=test.copy()
retest['predict']=result
acc = (retest.iloc[:,-1]==retest.iloc[:,-2]).mean()
print(f'逻辑回归模型的准确率={acc}')
return retest
# 导入数据集
train = pd.read_table('horseColicTraining.txt',header=None)
test = pd.read_table('horseColicTest.txt',header=None)
# 调用
get_acc(train,test,alpha=0.0001, maxCycles=50000)
运行结果

注:因为这里的测试准确率表示从测试集中抽取的,所以准确率相对前面的较低。
4 逻辑回归算法的优缺点
优点:计算代价不高,易于理解和实现;
缺点:容易欠拟合,分类精度可能不高;
适用数据类型:数值型和标称型数据。
参考资料
[1] 机器学习实战. 人民邮电出版社.
[2] 机器学习, 北京: 清华大学出版社, 2016年1月
[3] 机器学习(西瓜书). 公式推导解析
[4] https://live.bilibili.com/14988341