AC自动机算法详解
如果你对KMP算法和了解的话,应该知道KMP算法中的next函数(shift函数或者fail函数)是干什么用的。KMP中我们用两个指针i和j分别表示,A[i-j+ 1..i]与B[1..j]完全相等。也就是说,i是不断增加的,随着i的增加j相应地变化,且j满足以A[i]结尾的长度为j的字符串正好匹配B串的前 j个字符,当A[i+1]≠B[j+1],KMP的策略是调整j的位置(减小j值)使得A[i-j+1..i]与B[1..j]保持匹配且新的B[j+1]恰好与A[i+1]匹配,而next函数恰恰记录了这个j应该调整到的位置。同样AC自动机的失败指针具有同样的功能,也就是说当我们的模式串在Tire上进行匹配时,如果与当前节点的关键字不能继续匹配的时候,就应该去当前节点的失败指针所指向的节点继续进行匹配。
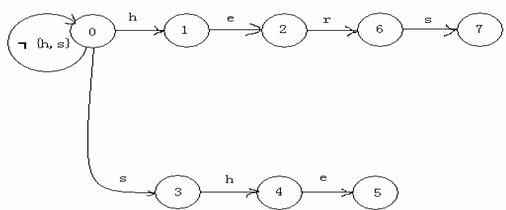
看下面这个例子:给定5个单词:say she shr he her,然后给定一个字符串yasherhs。问一共有多少单词在这个字符串中出现过。我们先规定一下AC自动机所需要的一些数据结构,方便接下去的编程。
2 struct node{
3 node * fail; // 失败指针
4 node * next[kind]; // Tire每个节点的个子节点(最多个字母)
5 int count; // 是否为该单词的最后一个节点
6 node(){ // 构造函数初始化
7 fail = NULL;
8 count = 0 ;
9 memset(next,NULL, sizeof (next));
10 }
11 } * q[ 500001 ]; // 队列,方便用于bfs构造失败指针
12 char keyword[ 51 ]; // 输入的单词
13 char str[ 1000001 ]; // 模式串
14 int head,tail; // 队列的头尾指针
有了这些数据结构之后,就可以开始编程了:
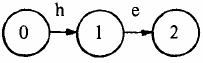
首先,将这5个单词构造成一棵Tire,如图-1所示。
2 node * p = root;
3 int i = 0 ,index;
4 while (str[i]){
5 index = str[i] - ' a ' ;
6 if (p -> next[index] == NULL) p -> next[index] = new node();
7 p = p -> next[index];
8 i ++ ;
9 }
10 p -> count ++ ; // 在单词的最后一个节点count+1,代表一个单词
11 }
在构造完这棵Tire之后,接下去的工作就是构造下失败指针。构造失败指针的过程概括起来就一句话:设这个节点上的字母为C,沿着他父亲的失败指针走,直到走到一个节点,他的儿子中也有字母为C的节点。然后把当前节点的失败指针指向那个字母也为C的儿子。如果一直走到了root都没找到,那就把失败指针指向root。具体操作起来只需要:先把root加入队列(root的失败指针指向自己或者NULL),这以后我们每处理一个点,就把它的所有儿子加入队列,队列为空。
2 int i;
3 root -> fail = NULL;
4 q[head ++ ] = root;
5 while (head != tail){
6 node * temp = q[tail ++ ];
7 node * p = NULL;
8 for (i = 0 ;i < 26 ;i ++ ){
9 if (temp -> next[i] != NULL){
10 if (temp == root) temp -> next[i] -> fail = root;
11 else {
12 p = temp -> fail;
13 while (p != NULL){
14 if (p -> next[i] != NULL){
15 temp -> next[i] -> fail = p -> next[i];
16 break ;
17 }
18 p = p -> fail;
19 }
20 if (p == NULL) temp -> next[i] -> fail = root;
21 }
22 q[head ++ ] = temp -> next[i];
23 }
24 }
25 }
26 }
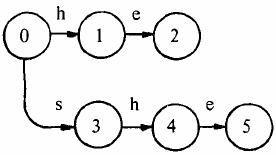
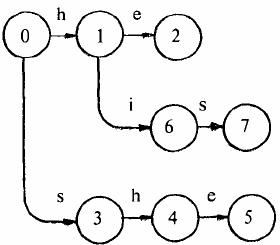
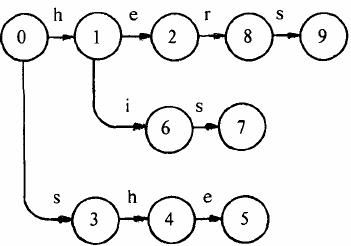
从代码观察下构造失败指针的流程:对照图-2来看,首先root的fail指针指向NULL,然后root入队,进入循环。第1次循环的时候,我们需要处理2个节点:root->next[‘h’-‘a’](节点h) 和 root->next[‘s’-‘a’](节点s)。把这2个节点的失败指针指向root,并且先后进入队列,失败指针的指向对应图-2中的(1),(2)两条虚线;第2次进入循环后,从队列中先弹出h,接下来p指向h节点的fail指针指向的节点,也就是root;进入第13行的循环后,p=p->fail也就是p=NULL,这时退出循环,并把节点e的fail指针指向root,对应图-2中的(3),然后节点e进入队列;第3次循环时,弹出的第一个节点a的操作与上一步操作的节点e相同,把a的fail指针指向root,对应图-2中的(4),并入队;第4次进入循环时,弹出节点h(图中左边那个),这时操作略有不同。在程序运行到14行时,由于p->next[i]!=NULL(root有h这个儿子节点,图中右边那个),这样便把左边那个h节点的失败指针指向右边那个root的儿子节点h,对应图-2中的(5),然后h入队。以此类推:在循环结束后,所有的失败指针就是图-2中的这种形式。
最后,我们便可以在AC自动机上查找模式串中出现过哪些单词了。匹配过程分两种情况:(1)当前字符匹配,表示从当前节点沿着树边有一条路径可以到达目标字符,此时只需沿该路径走向下一个节点继续匹配即可,目标字符串指针移向下个字符继续匹配;(2)当前字符不匹配,则去当前节点失败指针所指向的字符继续匹配,匹配过程随着指针指向root结束。重复这2个过程中的任意一个,直到模式串走到结尾为止。
2 int i = 0 ,cnt = 0 ,index,len = strlen(str);
3 node * p = root;
4 while (str[i]){
5 index = str[i] - ' a ' ;
6 while (p -> next[index] == NULL && p != root) p = p -> fail;
7 p = p -> next[index];
8 p = (p == NULL) ? root:p;
9 node * temp = p;
10 while (temp != root && temp -> count !=- 1 ){
11 cnt += temp -> count;
12 temp -> count =- 1 ;
13 temp = temp -> fail;
14 }
15 i ++ ;
16 }
17 return cnt;
18 }
到此为止AC自动机算法的详细过程已经全部介绍结束,看一道例题: http://acm.hdu.edu.cn/showproblem.php?pid=2222
Wiskey also wants to bring this feature to his image retrieval system.
Every image have a long description, when users type some keywords to find the image, the system will match the keywords with description of image and show the image which the most keywords be matched.
To simplify the problem, giving you a description of image, and some keywords, you should tell me how many keywords will be match.
Each case will contain two integers N means the number of keywords and N keywords follow. (N <= 10000)
Each keyword will only contains characters 'a'-'z', and the length will be not longer than 50.
The last line is the description, and the length will be not longer than 1000000.
15shehesayshrheryasherhs
3
2 using namespace std;
3
4 const int kind = 26 ;
5 struct node{
6 node * fail; // 失败指针
7 node * next[kind]; // Tire每个节点的26个子节点(最多26个字母)
8 int count; // 是否为该单词的最后一个节点
9 node(){ // 构造函数初始化
10 fail = NULL;
11 count = 0 ;
12 memset(next,NULL, sizeof (next));
13 }
14 } * q[ 500001 ]; // 队列,方便用于bfs构造失败指针
15 char keyword[ 51 ]; // 输入的单词
16 char str[ 1000001 ]; // 模式串
17 int head,tail; // 队列的头尾指针
18
19 void insert( char * str,node * root){
20 node * p = root;
21 int i = 0 ,index;
22 while (str[i]){
23 index = str[i] - ' a ' ;
24 if (p -> next[index] == NULL) p -> next[index] = new node();
25 p = p -> next[index];
26 i ++ ;
27 }
28 p -> count ++ ;
29 }
30 void build_ac_automation(node * root){
31 int i;
32 root -> fail = NULL;
33 q[head ++ ] = root;
34 while (head != tail){
35 node * temp = q[tail ++ ];
36 node * p = NULL;
37 for (i = 0 ;i < 26 ;i ++ ){
38 if (temp -> next[i] != NULL){
39 if (temp == root) temp -> next[i] -> fail = root;
40 else {
41 p = temp -> fail;
42 while (p != NULL){
43 if (p -> next[i] != NULL){
44 temp -> next[i] -> fail = p -> next[i];
45 break ;
46 }
47 p = p -> fail;
48 }
49 if (p == NULL) temp -> next[i] -> fail = root;
50 }
51 q[head ++ ] = temp -> next[i];
52 }
53 }
54 }
55 }
56 int query(node * root){
57 int i = 0 ,cnt = 0 ,index,len = strlen(str);
58 node * p = root;
59 while (str[i]){
60 index = str[i] - ' a ' ;
61 while (p -> next[index] == NULL && p != root) p = p -> fail;
62 p = p -> next[index];
63 p = (p == NULL) ? root:p;
64 node * temp = p;
65 while (temp != root && temp -> count !=- 1 ){
66 cnt += temp -> count;
67 temp -> count =- 1 ;
68 temp = temp -> fail;
69 }
70 i ++ ;
71 }
72 return cnt;
73 }
74 int main(){
75 int n,t;
76 scanf( " %d " , & t);
77 while (t -- ){
78 head = tail = 0 ;
79 node * root = new node();
80 scanf( " %d " , & n);
81 getchar();
82 while (n -- ){
83 gets(keyword);
84 insert(keyword,root);
85 }
86 build_ac_automation(root);
87 scanf( " %s " ,str);
88 printf( " %d\n " ,query(root));
89 }
90 return 0 ;
91 }
AC算法是Alfred V.Aho(《编译原理》(龙书)的作者),和Margaret J.Corasick于1974年提出(与KMP算法同年)的一个经典的多模式匹配算法,可以保证对于给定的长度为n的文本,和模式集合P{p1,p2,...pm},在O(n)时间复杂度内,找到文本中的所有目标模式,而与模式集合的规模m无关。正如KMP算法在单模式匹配方面的突出贡献一样,AC算法对于多模式匹配算法后续的发展也产生了深远的影响,而且更为重要的是,两者都是在对同一问题——模式串前缀的自包含问题的研究中,产生出来的,AC算法从某种程度上可以说是KMP算法在多模式环境下的扩展。在我的《KMP算法详解》一文中,我在最后已经提到,如果要用KMP算法匹配长度为n的文本中的m个模式,则需要为每一个模式维护一个next跳转表,在执行对文本的匹配过程中,我们需要关注所有这些next表的状态转移情况,这使得时间复杂度增长为O(mn),对于较大的模式集合来说,这样的时间增长可能是无法接受的。AC算法解决了这一问题,通过对模式集合P的预处理,去除了模式集合的规模对匹配算法速度的影响。
要理解AC算法,仍然需要对KMP算法的透彻理解。这里我们还是以KMP算法中的老例子来说明前缀自包含如何在AC算法中发挥作用。对于模式串"abcabcacab",我们知道非前缀子串abc(abca)cab是模式串的一个前缀(abca)bcacab,而非前缀子串ab(cabca)cab不是模式串abcabcacab的前缀,根据此点,我们构造了next结构,实现在匹配失败时的跳转。而对于多模式环境,这个情况会发生一定的变化。这里以AC论文中的例子加以说明,对于模式集合P{he,she,his,hers},模式s(he)的非前缀子串he,实际上却是模式(he),(he)rs的前缀。如果目标串target[i...i+2]与模式she匹配,同时也意味着target[i+1...i+2]与he,hers这两个模式的头两个字符匹配,所以此时对于target[i+3],我们不需要回溯目标串的当前位置,而直接将其与he,hers两个模式的第3个字符对齐,然后直接向后继续执行匹配操作。
经典的AC算法由三部分构成,goto表,fail表和output表,goto表是由模式集合P中的所有模式构成的状态转移自动机,以上面的集合为例,其对应的goto结果如下,其中圆圈对应自动机的各个状态,边对应当前状态输入的字符。
![]()
对于给定的集合P{p1,p2,...pm},构建goto表的步骤是,对于P中的每一个模式pi[1...j](1<=i
第一步,将模式he加入goto表:
![]()
第二步,将模式she加入goto表:
![]()
第三步,将模式his加入goto表:
![]()
第四步,将模式hers加入goto表:
![]()
对于第一和第二步而言,两个模式没有重叠的前缀部分,所以每输入一个字符,都对应一个新状态。第三步时,我们发现,D[0][p3[1]]=D[0]['h']=1,所以对于新模式p3的首字母'h',我们不需要新增加一个状态,而只需将D的当前状态转移到D[1]即可。而对于模式p4其前两个字符he使状态机转移至状态D[2],所以其第三字符对应的状态D[8]就紧跟在D[2]之后。
goto表构建完成之后,我们就要构建fail表,所谓的fail表就是当我们处在状态机的某个状态D[p]时,此时的输入字符c使得D[p][c]=0,那么我们应该转移到状态机的哪个位置来继续进行呢。以输入文本"shers"为例,当输入到字母e时,我们会发现匹配模式(she)rs,对应与状态机的状态D[5],然后输入字母r,此时我们发现D[6]['r']=0,对于字母r D[6]不存在有意义的跳转。此时我们不能跳转回状态D[0],这样就会丢掉可能的匹配s(hers)。我们发现s(he)的后缀he是模式(he)rs的一个前缀,所以当匹配模式she时,实际也已经匹配了模式hers的前缀he,此时我们可以将状态D[6]转移到hers中的前缀he在goto表中的对应状态D[2]处,再向后执行跳转匹配。这一跳转,就是AC算法中的fail跳转,要实现正确的fail跳转,还需要满足一系列条件,下面会逐一说明。
对于模式串she,其在字母e之后发生了匹配失败,此时其对应的模式串(回溯到状态D[0])就是she。对于she来说,它有两个包含后缀(除字符串自身外的所有后缀),he和e,对于后缀he,将其输入自动机D,从状态D[0]可以转移到状态D[2],对于后缀e,没有可行的状态转移方案。所以对于状态D[5],如果对于新输入的字符c没有可行的转移方案,我们可以跳转到状态D[2],考察D[2][c]是否等于0.
AC两人在论文中举出的例子,并不能涵盖在构建fail时遇到的所有情况,这里特别说明一下。前面我们说过,对于she的包含后缀e,没有可行的转移方案,此时如果模式串中还包含一个模式era,那么D[5]可不可以转移到状态D[10]去呢,实际上这是不行的,我们需要找到的是当前所有包含后缀中最长的满足条件者(拗口),如果D[5]对于失败的输入c优先转移到D[10],那么对于文本串shers,很显然会漏掉可能匹配hers,那么什么时机才应该转移到D[10]呢,当我们处理模式串hers时,处理到D[2]时对于之前的输入he,其最长的包含后缀是e,将e输入自动机,可以转移到D[10],所以在D[2]处发生匹配失败的时候才应该转移到D[10]。所以当我们在D[5]处匹配失败时,要先跳转到D[2]如果再没有可用的转移,再跳转到D[10]。
![]()
这个例子同时说明,对于模式集合P的所有模式pi,我们需要处理的不仅是pi的所有包含后缀,而是pi的所有非前缀子串。以模式hers为例,其在2,8,9三个状态都可能发生匹配失败,所以我们要提取出hers的所有非前缀子串(e,er,r,ers,rs,s),然后按照这些子串的末尾字符所对应的自动机状态分组(上例就可以分组为{e}对应状态2,{er,r}对应状态8,{ers,rs,s}对应状态9),然后分别将这些组中的子串从D[0]开始执行状态转移,直到没有可行的转移方案,或者整个序列使状态机最终转移到一个合法状态为止。如果一组中的所有子串都不能使状态机转移到一个合法状态,则这组子串所对应的状态的fail值为0,如果存在可行的状态转移方案,则选择其中最长的子串经过转移后的最终状态,令其对应的组的状态的fail值与其相等。
举例说明,当我们要处理模式串hers的fail表,假设已经构建好的goto表如前图所示,首先我们需要考察状态2,此时hers的输入字符是he,其所有包含后缀只有e,我们让e从D[0]开始转移,发现成功转移到D[10],所以fail[2]=10。然后我们考察状态8,此时hers的输入字符是her,所有包含后缀为er,r,因为我们要找到可以实现转移的最大包含后缀,所以我们先让er从D[0]开始转移,发现成功转移到D[11],所以fail[8]=11,这是虽然后缀e也可以成功转移到D[10],但是不是当前包含后缀分组中的子串所能实现的最长跳转,放弃。然后我们考察9,此时hers的输入字符串是hers,所有包含后缀为ers,rs,s,我们依次让其执行状态转换,发现s是可以实现转移的最长子串,转移到D[3],所以fail[9]=3。
我在《KMP算法详解》一文中讲到过一个找当前位置最大包含前缀的笨方法,现在我们构建fail表的方法,就是那一方法在多模式环境下的重新演绎。对于长度为n的模式串p而言,其所有非前缀子串的总数有(n^2-n)/2个,如果将这些子串都要经过状态机执行状态转移,时间复杂度为O(n^3),所以用这种方法,计算包含m个模式的模式集合P的fail表的时间复杂度为O(mn^3),如果包含10000个模式,模式的平均长度为10,计算fail表的运算就是千万级别,严重影响AC算法的实用价值。不过还好Aho,Corasick在自己的论文中同时给出了一个与模式串总长度相关的线性时间算法,可以参考我的这篇文章,但是这个方法的正确性不那么显而易见。不过这并非就意味着蛮力法就没有什么价值了,蛮力法一方面容易理解,可以为我们探索更高效的算法提供灵感,另一方面也可以帮助我们验证高效算法的正确性。
最后我们来说一下AC算法中的output表,在构建goto表的过程中,我们知道,状态2,5,7,9是输入的4个模式串的末尾部分,所以如果在执行匹配过程中,达到了如下四个状态,我们就知道对应的模式串被发现了。对于状态机D的某些状态,对应某个完整的模式串已经被发现,我们就用output表来记录这一信息。完成goto表的构建后,D中各状态对应的output表的情况如下:
2 he
5 she
7 his
9 hers
但是这并不是我们最终的output表。下面以构建状态5的fail表为例,说明一下fail表的构建是如何影响output表的。首先根据之前我们的介绍,当我们开始计算D[5]的fail值时,我们要将模式she的所有包含后缀提取出来,包括he,e。这里我们需要注意,在output表中,状态5是一个输出状态。当我们用he在状态机中执行转移时,我们会成功转移到2,这里output[2]也是一个输出状态,这就意味着在发现模式串she的同时,实际上也发现了模式串he,所以如果通过某种转换,我们到达了状态5,则意味着我们发现了she和he两个模式,此时fail[5]=2,所以我们需要将output[2]所包含的输出字符串加入到output[5]中。完成goto和fail表构建后,我们所得到的最终output表为:
2 he
5 she,he
7 his
9 hers
这实际上是一个后缀包含问题,也就是模式p1实际上是模式p2的后缀,所以当发现模式p2时,p1自然也被发现了。
AC算法对文本进行匹配的具体步骤是。一开始,将i指向文本text[1...j]的起始位置,然后用text[i]从goto表的状态D[0]开始执行状态跳转。如果存在可行的跳转方案D[0][text[i]]=p,p!=0,则将i增加1,同时转移到状态D[p]。如果不存在可行的转移方案,则考察状态D[p]的fail值,如果fail[p]不等于0,则转移到D[fail[p]],再次查看D[fail[p]][text[i]]是否等于0,直到发现不为0的状态转移方案或者对于所有经历过的fail状态,对于当前输入text[i]都没有非0的转移方案为止,如果确实不存在非0的转移方案,则将i增加1,同时转移到D[0]继续执行跳转。在每次跳转到一个状态D[p]时(fail跳转不算),都需要查看一下output[p]是否指向可输出的模式串,如果有,说明当前位置匹配了某些模式串,将这些模式串输出。
下面就是一个AC算法的简单示例,由于是示例程序,重在演示实现,所以做了一些简化,这里假设输入字符只包含小写英文字母(26个)。我用了一个二维数组来保存goto表信息,这样可以实现比较直接的跳转,缺点是浪费大量的内存空间。AC算法中goto表状态的数量,可以参考模式中所有的字符数,所以对于上万模式的应用场景,内存空间的占用会很惊人,如何既能存储如此多的状态,又能实现低成本的状态跳转,是一个需要研究的问题,后续我还会专门撰文介绍。
首先是程序中用到的goto,fail,output表结构和几个宏定义。
- #define ALPHABET_SIZE 26
- #define MAXIUM_STATES 100
- int _goto[MAXIUM_STATES][ALPHABET_SIZE];
- int _fail[MAXIUM_STATES];
- set
_out[MAXIUM_STATES];//使用set是因为在生成fail表,同时更新out表过程中,有可能向同一位置多次插入同一个模式串
然后是计算goto表的算法。
- inline void BuildGoto(const vector
& patterns) - {
- unsigned int used_states;
- unsigned int t;
- vector
::const_iterator vit; - string::const_iterator sit;
- for(vit = patterns.begin(), used_states = 0; vit != patterns.end(); ++vit)
- {
- for(sit = vit->begin(), t = 0; sit != vit->end(); ++sit)
- {
- if(_goto[t][(*sit)-'a'] == 0)
- {
- _goto[t][(*sit)-'a'] = ++used_states;
- t = used_states;
- }
- else
- {
- t = _goto[t][(*sit)-'a'];
- }
- }
- _out[t].insert(*vit);
- }
- }
然后是计算fail表的算法。
- inline void BuildFail(const vector
& patterns) - {
- unsigned int t, m, last_state;
- unsigned int s[20];
- vector
::const_iterator vit; - string::const_iterator sit1, sit2, sit3;
- for(vit = patterns.begin(); vit != patterns.end(); ++vit)
- {
- //先要找到输入的单词的各字母对应的状态转移表的状态号,由于状态转移表没有
- //记录各状态的前驱状态信息,该步暂时无法掠过
- t = 0;
- m = 0;
- sit1 = vit->begin();
- while(sit1 != vit->end() && _goto[t][*sit1 - 'a'] != 0)
- {
- t = _goto[t][*sit1 - 'a'];
- ++sit1;
- s[m++] = t;
- }
- for(sit1 = vit->begin() + 1; sit1 != vit->end(); ++sit1)
- {
- //此时的[sit2, sit1+1)就是当前模式的一个非前缀子串
- for(sit2 = vit->begin() + 1; sit2 != sit1 + 1; ++sit2)
- {
- t = 0;
- sit3 = sit2;
- //对该子串在goto表中执行状态转移
- while(sit3 != sit1 + 1 && _goto[t][*sit3 - 'a'] != 0)
- {
- t = _goto[t][*sit3 - 'a'];
- ++sit3;
- }
- //当前子串可以使goto表转移到一个非0位置
- if(sit3 == sit1 + 1)
- {
- //求出输入当前子串在goto表中所转移到的位置
- last_state = s[sit3-vit->begin() - 1];
- //更新该位置的fail值,如果改为值得fail值为0,则用t值替换,因为对于sit1而言,是按照以其为末尾元素的非前缀
- //子串的由长到短的顺寻在goto表中寻找非0状态转移的,而满足条件的t是这里免得最长子串
- if(_fail[last_state] == 0)
- {
- _fail[last_state] = t;
- }
- //如果两者都标识完整的模式串
- if(_out[last_state].size() > 0 && _out[t].size() > 0)
- {
- //将out[t]内的模式串全部加入out[last_state]中
- for(set
::const_iterator cit = _out[t].begin(); cit != _out[t].end(); ++cit) - {
- _out[last_state].insert(*cit);
- }
- }
- }
- }
- }
- }
- }
然后是执行多模式匹配的AC算法。
- void AC(const string& text, const vector
& patterns) - {
- unsigned int t = 0;
- string::const_iterator sit = text.begin();
- BuildGoto(patterns);
- BuildFail(patterns);
- //每次循环中,t都是*sit的前置状态
- while(sit != text.end())
- {
- //检查是否发现了匹配模式,如果有,将匹配输出
- if(_out[t].size() > 0)
- {
- cout << (sit - text.begin() - 1) << ": ";
- for(set
::const_iterator cit = _out[t].begin(); cit != _out[t].end(); ++cit) - {
- cout << (*cit) << ", ";
- }
- cout << '\n';
- }
- if(_goto[t][*sit - 'a'] == 0)
- {
- t = _fail[t];
- //找到可以实现非0跳转的fail状态转移
- while(t != 0 && _goto[t][*sit - 'a'] == 0)
- {
- t = _fail[t];
- }
- if(t == 0)
- {
- //跳过那些在初始状态不能实现非0状态跳转的字母输入
- if(_goto[0][*sit - 'a'] == 0)
- {
- ++sit;
- }
- continue;
- }
- }
- t = _goto[t][*sit - 'a'];
- ++sit;
- }
- }
后记:
- KMP算法依然是解读AC算法的重要线索,前缀,子串,后缀永远和模式匹配纠缠在一起。
- AC状态机实际上更适合用Trie结构来存储。
- 可以将算法中使用到的goto,fail,output三张表以离线的方式计算出来保存在一个文件中,当AC算法启动时,直接从文件中读取三个表的内容,这样可以有效减少每次AC算法启动时都需要构建三个表所花费的时间。
KMP算法,是由Knuth,Morris,Pratt共同提出的模式匹配算法,其对于任何模式和目标序列,都可以在线性时间内完成匹配查找,而不会发生退化,是一个非常优秀的模式匹配算法。但是相较于其他模式匹配算法,该算法晦涩难懂,第一次接触该算法的读者往往会看得一头雾水,主要原因是KMP算法在构造跳转表next过程中进行了多个层面的优化和抽象,使得KMP算法进行模式匹配的原理显得不那么直白。本文希望能够深入KMP算法,将该算法的各个细节彻底讲透,扫除读者对该算法的困扰。
KMP算法对于朴素匹配算法的改进是引入了一个跳转表next[]。以模式字符串abcabcacab为例,其跳转表为:
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pattern[j] | a | b | c | a | b | c | a | c | a | b |
| next[j] | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 1 |
举例说明,如下是使用上例的模式串对目标串执行匹配的步骤
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| b | a | b | c | b | a | b | c | a | b | c | a | a | b | c | a | b | c | a | b | c | a | c | a | b | c |
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b |
next跳转表,在进行模式匹配,实现模式串向后移动的过程中,发挥了重要作用。这个表看似神奇,实际从原理上讲并不复杂,对于模式串而言,其前缀字符串,有可能也是模式串中的非前缀子串,这个问题我称之为前缀包含问题。以模式串abcabcacab为例,其前缀4 abca,正好也是模式串的一个子串abc(abca)cab,所以当目标串与模式串执行匹配的过程中,如果直到第8个字符才匹配失败,同时也意味着目标串当前字符之前的4个字符,与模式串的前4个字符是相同的,所以当模式串向后移动的时候,可以直接将模式串的第5个字符与当前字符对齐,执行比较,这样就实现了模式串一次性向前跳跃多个字符。所以next表的关键就是解决模式串的前缀包含。当然为了保证程序的正确性,对于next表的值,还有一些限制条件,后面会逐一说明。
如何以较小的代价计算KMP算法中所用到的跳转表next,是算法的核心问题。这里我们引入一个概念f(j),其含义是,对于模式串的第j个字符pattern[j],f(j)是所有满足使pattern[1...k-1] = pattern[j-(k-1)...j - 1](k < j)成立的k的最大值。还是以模式串abcabcacab为例,当处理到pattern[8] = 'c'时,我们想找到'c'前面的k-1个字符,使得pattern[1...k-1] = pattern[8-(k-1)...7],这里我们可以使用一个笨法,让k-1从1到6递增,然后依次比较,直到找到最大值的k为止,比较过程如下
| k-1 | 前缀 | 关系 | 子串 |
| 1 | a | == | a |
| 2 | ab | != | ca |
| 3 | abc | != | bca |
| 4 | abca | == | abca |
| 5 | abcab | != | cabca |
| 6 | abcabc | != | bcabca |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pattern[j] | a | b | c | a | b | c | a | c | a | b |
| next[j] | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 1 |
| f(j) | 0 | 1 | 1 | 1 | 2 | 3 | 4 | 5 | 1 | 2 |
如果 pattern[j] != pattern[f(j)],next[j] = f(j);
如果 pattern[j] = pattern[f(j)],next[j] = next[f(j)];
当要求f(9)时,f(8)和next[8]已经可以得到,此时我们可以考察pattern[next[8]],根据前面对于next值的计算方式,我们知道pattern[8] != pattern[next[8]]。我们的目的是要找到pattern[9]的包含前缀,而pattern[8] != pattern[5],pattern[1...5]!=pattern[4...8]。我们继续考察pattern[next[5]]。如果pattern[8] = pattern[next[5]],假设next[5] = 3,说明pattern[1...2] = pattern[6...7],且pattern[3] = pattern[8],此时对于pattern[9]而言,就有pattern[1...3]=pattern[6...8],我们就找到了f(9) = 4。这里我们考察的是pattern[next[j]],而不是pattern[f(j)],这是因为对于next[]而言,pattern[j] != pattern[next[j]],而对于f()而言,pattern[j]与pattern[f(j)]不一定不相等,而我们的目的就是要在pattern[j] != pattern[f(j)]的情况下,解决f(j+1)的问题,所以使用next[j]向前回溯,是正确的。
现在,我们来总结一下next[j]和f(j)的关系,next[j]是所有满足pattern[1...k - 1] = pattern[(j - (k - 1))...j -1](k < j),且pattern[k] != pattern[j]的k中,k的最大值。而f(j)是满足pattern[1...k - 1] = pattern[(j - (k - 1))...j -1](k < j)的k中,k的最大值。还是以上例的模式来说,对于第7个元素,其f(j) = 4, 说明pattern[7]的前3个字符与模式的前缀3相同,但是由于pattern[7] = pattern[4], 所以next[7] != 4。
通过以上这些,读者可能会有疑问,为什么不用f(j)直接作为KMP算法的跳转表呢?实际从程序正确性的角度讲是可以的,但是使用next[j]作为跳转表更加高效。还是以上面的模式为例,当target[n]与pattern[7]发生匹配失败时,根据f(j),target[n]要继续与pattern[4]进行比较。但是在计算f(8)的时候,我们会得出pattern[7] = pattern[4],所以target[n]与pattern[4]的比较也必然失败,所以target[n]与pattern[4]的比较是多余的,我们需要target[n]与更小的pattern进行比较。当然使用f(j)作为跳转表也能获得不错的性能,但是KMP三人将问题做到了极致。
我们可以利用f(j)作为媒介,来递推模式的跳转表next。算法如下:
- inline void BuildNext(const char* pattern, size_t length, unsigned int* next)
- {
- unsigned int i, t;
- i = 1;
- t = 0;
- next[1] = 0;
- while(i < length + 1)
- {
- while(t > 0 && pattern[i - 1] != pattern[t - 1])
- {
- t = next[t];
- }
- ++t;
- ++i;
- if(pattern[i - 1] == pattern[t - 1])
- {
- next[i] = next[t];
- }
- else
- {
- next[i] = t;
- }
- }
- //pattern末尾的结束符控制,用于寻找目标字符串中的所有匹配结果用
- while(t > 0 && pattern[i - 1] != pattern[t - 1])
- {
- t = next[t];
- }
- ++t;
- ++i;
- next[i] = t;
- }
inline void BuildNext(const char* pattern, size_t length, unsigned int* next)
{
unsigned int i, t;
i = 1;
t = 0;
next[1] = 0;
while(i < length + 1)
{
while(t > 0 && pattern[i - 1] != pattern[t - 1])
{
t = next[t];
}
++t;
++i;
if(pattern[i - 1] == pattern[t - 1])
{
next[i] = next[t];
}
else
{
next[i] = t;
}
}
//pattern末尾的结束符控制,用于寻找目标字符串中的所有匹配结果用
while(t > 0 && pattern[i - 1] != pattern[t - 1])
{
t = next[t];
}
++t;
++i;
next[i] = t;
}
程序中,9到27行的循环需要特别说明一下,我们发现在循环开始之后,就没有再为t赋新值,也就是说,对于计算next[j]时的t值,在计算next[j+1]时,还会用得着。实际这时的t的就等于f(j)。还是以上例的目标串为例,当j等于1,我们可以得出t = f(2) = 1。使用归纳法,当计算完next[j]后,我们假设此时t=f(j),此时第11~14行的循环就是要找到满足pattern[k] = pattern[j]的最大k值。如果这样的k存在,对于pattern[j+1]而言,其前k个元素,与模式的前缀k相同。此时的t+1就是f(j+1)。这时我们就要判断pattern[j+1]和pattern[t](t = t+1)的关系,然后求出next[j+1]。这里需要初始条件next[1] = 0。
利用跳转表实现字符串匹配的算法如下:
- unsigned int KMP(const char* text, size_t text_length, const char* pattern, size_t pattern_length, unsigned int* matches)
- {
- unsigned int i, j, n;
- unsigned int next[pattern_length + 2];
- BuildNext(pattern, pattern_length, next);
- i = 0;
- j = 1;
- n = 0;
- while(pattern_length + 1 - j <= text_length - i)
- {
- if(text[i] == pattern[j - 1])
- {
- ++i;
- ++j;
- //发现匹配结果,将匹配子串的位置,加入结果
- if(j == pattern_length + 1)
- {
- matches[n++] = i - pattern_length;
- j = next[j];
- }
- }
- else
- {
- j = next[j];
- if(j == 0)
- {
- ++i;
- ++j;
- }
- }
- }
- //返回发现的匹配数
- return n;
- }
unsigned int KMP(const char* text, size_t text_length, const char* pattern, size_t pattern_length, unsigned int* matches)
{
unsigned int i, j, n;
unsigned int next[pattern_length + 2];
BuildNext(pattern, pattern_length, next);
i = 0;
j = 1;
n = 0;
while(pattern_length + 1 - j <= text_length - i)
{
if(text[i] == pattern[j - 1])
{
++i;
++j;
//发现匹配结果,将匹配子串的位置,加入结果
if(j == pattern_length + 1)
{
matches[n++] = i - pattern_length;
j = next[j];
}
}
else
{
j = next[j];
if(j == 0)
{
++i;
++j;
}
}
}
//返回发现的匹配数
return n;
}
该算法在原有基础上进行了扩展,在原模式串末尾加入了一个“空字符”,“空字符”不等于任何的可输入字符,当目标串匹配至“空字符”时,说明已经在目标字符串中发现了模式,将模式串在目标串中的位置,加入matchs[]数组中,同时判定为匹配失败,并根据“空字符”的next值,跳转到适当位置,这样算法就可以识别出字符串中所有的匹配子串。
最后,对KMP算法的正确性做一简要说明,还是以上文的模式串pattern和目标串target为例,假设已经匹配到第3部的位置,且在target[13]处发现匹配失败,我们如何决定模式串的滑动步数,来保证既要忽略不必要的多余比较,又不漏过可能的匹配呢?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
| target | b | a | b | c | b | a | b | c | a | b | c | a | a | b | c | a | b | c | a | b | c | a | c | a | b | c |
| pattern | a | b | c | a | b | c | a | c | a | b |
对于例子中的情况,显然向后移动多于3个字符有可能会漏过target[9...18]这样的的可能匹配。但是为什么向后移动1个或者2个字符是不必要的多余比较呢?当target[13]与pattern[8]匹配失败时,同时也意味着,target[6...12] = pattern[1...7],而next[8]=5,意味着,pattern[1...4] = pattern[4...7],pattern[1...5] != pattern[3...7],pattern[1...6] != pattern[2...7]。如果我们将模式串后移1个字符,使pattern[7]与target[13]对齐,此时target[7...12]相当于pattern[2...7],且target[7...12]与pattern[1..6]逐个对应,而我们已经知道pattern[1...6] != pattern[2...7]。所以不管target[13]是否等于pattern[7],此次比较都必然失败。同理向前移动2个字符也是多余的比较。由此我们知道当在pattern[j]处发生匹配失败时,将当前输入字符与pattern[j]和pattern[next[j]]之间的任何一个字符对齐执行的匹配尝试都是必然失败的。这就说明,在模式串从目标串头移动到目标串末尾的过程中,除了跳过了必然失败的情况之外,没有漏掉任何一个可能匹配,所以KMP算法的正确性是有保证的。
后记:
- 首先要感谢Knuth-Morris-Pratt那篇光辉的论文《Fast Pattern Matching In Strings》,让我们在字符串处理的道路上看得更远。本文的例子和思路,均完全来自这篇论文,论文后面还对KMP算法的时间复杂度进行了彻底的分析。
- KMP算法是一个高度优化的精妙算法,所以初涉该算法的时候,不要指望一蹴而就,一下子就将KMP算法理解透,而是应该循序渐进,逐步加深理解。据说该算法是Knuth,Morris,Pratt三人分别独立发现的,我斗胆揣测一下该算法的演进历程。首先应该是发现了模式串前缀的自包含问题,然后是提出了f(j)的概念,然后是搞定了如何计算f(j),然后提出了next[j]的概念,然后搞定了如何用f(j)计算next[j+1],然后是只用f(j)做中间结果直接算出next[j+1]。之所以我会这么猜测,主要是因为next跳转表的概念和生成算法太高端,中间经历了多个转换,极难一步到位想出来这么搞。所以我们也应该按照这个流程来学习KMP算法,而如何计算f(j)则是整个算法的精髓所在。
- 实际上,KMP算法中所用到的跳转表next是一个简化了的DFA,对于DFA而言,其跳转和输入的字符集有关,而KMP算法中的跳转表,对于模式串中的当前位置j-1,只有两种跳转方式pattern[j],和^pattern[j],所以KMP算法的跳转功能要弱于DFA,但是其构建速度,又大大快于DFA,在花费较小代价的同时,取得了逼近DFA的效果。下面是对于文中使用的模式串生成跳转表(上)和DFA的比较,显然DFA要复杂的多(这个是我手画的如果有画错的地方,请读者不吝赐教)。
今天说说多模式匹配AC算法(Aho and Corasick),感谢追风侠帮忙整理资料,while(1) {Juliet.say("3Q");}。前面学习了BM、Wu-Manber算法,WM由BM派生,不过AC与它们无染,是另外一种匹配思路。
| 1. 初识AC算法 |
Step1: 将由patterns组成的集合(要同时匹配多个patterns嘛)构成一个有限状态自动机。
Step2: 将要匹配的text作为自动机输入,输出含有哪些patterns及patterns在全文中位置。
自动机的执行动作由三个部分组成:
(1) 一个goto function
(2) 一个failure function
(3) 一个output function
我们先通过一个具体实例来了解一下这三个部分,及该自动机的运作方式。先有个大概印象,后面会具体讲解。patterns集合{he, she, his ,hers},我们要在”ushers”中查找并匹配。
![]()
(1) goto function
i 1 2 3 4 5 6 7 8 9
f(i) 0 0 0 1 2 0 3 0 3 (发现没?貌似i和f(i)有相同前缀哦^_^)
(2) failure function
i output(i)
2 {he}
5 {she,he}
7 {his}
9 {hers}
(3) output function
首先我们从状态0开始,接收匹配字符串的第一个字符u,在goto(简称goto function)中可以看到回到状态0,接着第二个字符s,发现转到状态3,在output中查找一下output(3)为空字符串,说明没有匹配到patterns。继续匹配h,转到状态4,查找output发现仍然没有匹配,继续字符e,状态转到了5,查找output,发现output(5)匹配了两个字符串she和he,并输出在整个字符串中的位置。然后接着匹配r,但发现g(5,r)=fail,这时候我们需要查找failure,发现f(5)=2,所以就转到状态2,并接着匹配r,状态转移到了8,接着匹配s,状态转移到了9,查看output,并输出output(9):hers,记录下匹配位置。至此字符串ushers匹配完毕。
具体的匹配算法如下:
| 算法1. Pattern matching machine 输入:text和M。text是x=a1a2...an,M是模式匹配自动机(包含了goto函数g(),failure函数f(),output函数output()) 输出:text中出现的pat以及其位置。
state←0 for i←1 until n do //吞入text的ai while g(state, ai)=fail state←f(state) //直到能走下去,呵呵,至少0那个状态怎么着都能走下去 state←g(state,ai) //得到下一个状态 if output(state)≠empty //能输出就输出 print i; print output(state) |
AC算法的时间复杂度是O(n),与patterns的个数及长度都没有关系。因为Text中的每个字符都必须输入自动机,所以最好最坏情况下都是O(n),加上预处理时间,那就是O(M+n),M是patterns长度总和。
| 2. 构造三表 |
OK,下面我们看看如何通过patterns集合构造上面的3个function
这三个function的构造分两个阶段:
(1) 我们决定状态和构造goto function
(2) 我们计算得出failure function
而output function的构造贯穿于这两个阶段中。
| 2.1 goto 与 ouput填表 |
我们仍然拿实例来一步步构造:patterns集合{he,she,his,hers}
首先我们构造patterns he
然后接着构造she
再构造his,由于在构造his的时候状态0接收h已经能到状态1,所以就不用重新建一个状态了,有点像建trie树的过程,共用一段相同的前缀部分
最后构造hers
具体构造goto function算法如下:
| 算法2. Construction of the goto function 输入:patterns集合K={y1,y2,...,yk} 输出:goto function g 和output function output的中间结果
/* We assume output(s) is empty when state s is first created, and g(s,a)=fail if a is undefined or if g(s,a) has not yet been defined. The procedure enter(y) inserts into the goto graph a path that spells out y. */
newstate←0 fori ← 1until k //对每个模式走一下enter(yi),要插到自动机里来嘛 enter(yi) for all a such that g(0,a)=fail g(0,a)←0
enter(a1a2...am) { state←0;j←;1 while g(state,aj)≠fail //能走下去,就尽量延用以前的老路子,走不下去,就走下面的for()拓展新路子 state←g(state,aj) j←j+1
for p←j until m //拓展新路子 newstate←newstate+1 g(state,ap)←newstate state←newstate
output(state)←{a1a2...am} //此处state为每次构造完一个pat时遇到的那个状态 } |
| 2.2 Failure 与 output填表 |
Failure function的构造:(这个比较抽象)
大家注意状态0不在failure function中,下面开始构造,首先对于所有depth为1的状态s,f(s)=0,然后归纳为所有depth为d的状态的failure值都由depth-1的状态得到。
具体讲,在计算depth为d的所有状态时候,我们会考虑到每一个depth为d-1的状态r
1. 如果对于所有的字符a,g(r,a)=fail,那么什么也不做,我认为这时候r已经是trie树的叶子结点了。
2. 否则的话,如果有g(r,a)=s,那么执行下面三步
(a) 设置state=f(r) //用state记录跟r共前缀的东东
(b) 执行state=f(state)零次或若干次,直到使得g(state,a)!=fail(这个状态一定会有的因为g(0,a)!=fail)//必须找条活路,能走下去的
(c) 设置f(s)=g(state,a),即相当于找到f(s)也是由一个状态匹配a字符转到的状态。
实例分析:
首先我们将depth为1的状态f(1)=f(3)=0,然后考虑depth为2的结点2,6,4
计算f(2)时候,我们设置state=f(1)=0,因为g(0,e)=0,所以f(2)=0;
计算f(6)时候,我们设置state=f(1)=0,因为g(0,i)=0,所以f(6)=0;
计算f(4)时候,我们设置state=f(3)=0,因为g(0,h)=1,所以f(4)=1;
然后考虑depth为3的结点8,7,5
计算f(8)时候,我们设置state=f(2)=0,因为g(0,r)=0,所以f(8)=0;
计算f(7)时候,我们设置state=f(6)=0,因为g(0,s)=3,所以f(7)=3;
计算f(5)时候,我们设置state=f(4)=1,因为g(1,e)=2,所以f(5)=2;
最后考虑depth为4的结点9
计算f(9)时候,我们设置state=f(8)=0,因为g(0,s)=3,所以f(9)=3;
具体算法:
| 算法3. Construction of the failure function 输入:goto function g and output function output from 算法2 输出:failure function f and output function output
queue←empty for each a such that g(0,a)=s≠0//其实这是广搜BFS的过程 queue←queue∪{s} f(s)←0
while queue≠empty pop(); for each a such that g(r,a)=s≠fail //r是队列头状态,如果r遇到a能走下去 queue←queue∪{s} //那就走 state←f(r) //与r同前缀的state while g(state,a)=fail //其实一定能找着不fail的,因为至少g(0,a)不会fail state←f(state)
f(s)←g(state,a) //OK,这一步相当于找到了s的同前缀状态,即f(s)
output(s)←output(s)∪output(f(s)) //建议走一下例子中g(4,e)=5的例子,然后ouput(5)∪output(2)={she,he} |
| 2.3 output |
Output function的构造参见算法2,3
| 3. 算法优化 |
改进1:观察一下算法3中的failure function还不够优化
我们可以看到g(4,e)=5,如果现在状态到了4并且当前的字符为t!=e,因为g(4,t)=fail,
所以就根据f(4)=1,跳转到状态1,而之前已经知道t!=e,所以就没必要跳到1,而直接跳到状态f(1)=0。
为了避免不必要的状态迁移,和KMP算法有异曲同工之处。重新定义了一个failure function:f1
| f1(1)=0, 对于i>1,如果能使状态f(i)转移的所有字符也能使i状态转移,那么f1(i)=f1(f(i)), 否则f1(i)=f(i)。 |
改进2:由于goto function中并不是每个状态对应任何一个字符都有状态迁移的,当迁移为fail的时候,我们就要查failure function,然后换个状态迁移。现在我们根据goto function和failure function来构造一个确定的有限自动机next move function,该自动机的每个状态遇到每个字符都可以进行状态迁移,这样就省略了failure function。
构造next move function的算法如下:
| 算法4:Construction of a deterministic finite automaton 输入:goto functioni g and failure function f 输出:next move function delta
queue←empty for each symbol a delta(0,a)←g(0,a) if g(0,a)≠0 queue←queue∪g(0,a)
while queue≠empty pop() for each symbol a if g(r,a)=s≠fail queue←queue∪{s} delta(r,a)←s else delta(r,a)←delta(f(r),a) |
Next function delta的计算如下:
其中’.’表示除了该状态能识别字符的其他字符。
改进2有利有弊:好处是能减少状态转移的次数;坏处是由于状态与状态之间的迁移多了,导致存储的空间比较大。
TTMP是啥意思呢?是Terminator Triggered Multi-Pattern 的意思,也就是结束符触发多模式算法。
-_-! 有点难理解,没关系,看完了也许就理解了。
不过这个自造的算法有点复杂,为了保证大家能够顺利阅读,请大家配合做一个测试:
拿出你的手表,或者其他计时器,看看你能用多块的时间阅读完下面这篇文章。
判断标准如下:
如果你的时间少于15秒,就可以不用读我的文章了,完全有能力造一个更强的算法;
如果你的时间少于30秒,我们可以沟通交流一下;
如果你的时间少于45秒,你可以仔细阅读一下,说不定可能也许有点启发作用;
如果你的时间少于60秒,你一定能够在这里挖到宝矿;
如果你不属于上述情况,我建议您啊,还是不要费力气阅读了,有点面为其难了。
Do you raelly know Engilsh?
At laest in Egnlish, wehn pepole raed, tehy
usaully wlil not noitce taht the charcatres bewteen
the frist ltteer and the lsat leettr are not in a
corrcet oredr. In fcat, hmuan brian does recongize
wrods by seeknig the fsirt ltteer and the lsat leettr,
and tehn fnidnig whcih charatcers are insdie of tehm.
See! All the wrods hree wtih mroe tahn 3 leettrs are
all wirtten in a worng way! Do you niotice taht?
嘿嘿!其实刚才那段能力测试的话是瞎扯的,主要是让大家快速阅读,而不是认真阅读。有意思吧?
这个不是我瞎扯出来的,是一个著名大学的研究结果(好像是剑桥),原文我没工夫找,瞎造一段对付一下。不知道你读上述文字的时候是什么感受,反正我自己觉得比较震撼,也比较有意思。
确实,如果按照自动机理论,一个字一个字的去认真阅读,那么也还是很有可能能够理顺语法结构,搞清楚一句话的含义的(理论上如此吧,实际上还没有任何一个机器能做到真人般的感知能力)。但是如果每个字都认真读,并查找语法表,一来速度会慢,二来需要海量的空间去做这个事情。而人脑比较聪明,经过若干年的锻炼之后,已经自动的学会了放弃细节,比如读"cerroct"这个词的时候,找到前面是c开头,后面是t结尾,中间有eoc各一个,r两个,一查表就知道肯定是“正确”这个词而不管他正确与否——哦,不好意思,我又写错了,应该是correct!
嗯?这个跟我们这次的主题——字符串多模式精确匹配,有什么关系呢?
有啊!当然有啦。不过在我告诉大家这个关系之前,我们先来分析一下,字符串多模式精确匹配的效率问题是什么?写之前我先给大家说一下,我下面的说明也许不会很严谨,因为有时候太严谨了,就不好理解了。例如什么令X=Y……反正我最近为了这个事情找的一些资料,尽是这个,看着也觉得头晕。
所谓字符串多模式精确匹配是啥意思呢?字符串不多说了,实际上能用于搜索字符串的,也能搜索其他东西。多模式嘛:比如
string s="xxx";
string t="xx";
s.IndexOf(t);
这个是在一个字符串s中,找出另外一个字符串t所在的位置(或者说是否存在),这种叫做单模式,只有一个要被寻找的字符串t——唯一的一个搜索模式;如果说是
string s="xxx";
string[] t= new string[]{"x1", "x2", "x3"...};
s.Scan(t);
这种呢,就叫做多模式匹配了。因为我要在s里面找出一组t中任意一个所在的位置,或者说是看看我们的文章里面是否有脏字表里面的敏感词汇。
关于多模匹配问题,有很多已有的算法,我没有仔细的看,只看了一个可能是WM的算法,实际上可能还有什么grep/agrep等算法。不过需要提醒大家的是,还有不少的算法是讨论模糊匹配的,比如说容许其中有一个字不正确,那些算法就不是我这个主题要讨论的内容了。我要讨论的是精确搜索,即要找“地瓜”就找“地瓜”,不要“地鼠”。
多模式精确匹配很难吗?不难,很简单:我们只需要循环一下,先找s.IndexOf(t1),再找s.IndexOf(t2)……但是如果你果然这么做,效率就会很低了,因为你会需要扫描文本很多很多遍。可以想象,我们的目标是只要扫描整个文章一遍就能够找出这个文章里面都有哪些敏感词汇。不过,很明显该目标并不容易达成,但至少我们可以尽量接近“只扫描一次”这个目标。在进一步分析之前,建议先看另外一篇文章:
(重发).NET脏字过滤算法
这篇文章的算法(比如叫做XDMP算法)其扫描速度已经是比较快的了,并且其思路也比较好理解,我们在这个文章的基础上进行讨论会比较有意义。首先我们先整理一下这个算法的思路:
1、首先 扫描文章里面的每一个字符,只有当某一个字符是脏字表中任意一个脏词的第一个字符(称为“ 起始符”),我们才试图看看接下来是否是脏字( 触发检索)。
2、但是我们也不是毫无头绪的就开始循环脏字表的每一个词条:
2.1、我们往后 检索一个字符,先看一下这个字符是否是脏字表里面的任意一个字符,如果不是,就表明不可能是脏字表中的任何一个条目,就可以退出了。
2.2、如果是,我们就取从第一个被检出字符到目前扫描到的字符之间的字符串,求哈希值,看看能否从哈希表中检出一个脏词。
如果检出了,那就大功告成,否则继续检索后面一个字符(重复2.1、2.2),直至找不到,或者超出脏字表条目最大的长度。
2.3、如果都找不到,或者超长,那么接下来就回到刚才的那个“ 起始符”后一个字符继续扫描(重复1、2),直至整个文章结束。
我这里先引入了三个重要概念:
1、扫描,指扫描文章,看看是否有需要和脏字表开始进行对比的情况;
2、检索,指已经发现可能存在情况了,在将文本和脏字表进行对比的过程;
3、起始符,指脏字表中条目中的第一个字符。
如果我们只要扫描,不需要检索就可以完成任务,那一定是最快的,不过目前我比较孤陋寡闻,没有找到这样的算法。
又或者,如果我们扫描一遍,而检索全中,那也很不错,很不幸,还是没见过。
很明显,扫描不应该多于1遍,否则肯定效率不可能高。那么检索就是算法的关键了!拆开来,提高检索质量有下列几个方式:
1、尽可能不触发检索;
2、如果确实需要触发检索了,那么每次触发检索的时候,要尽可能减少检索所需要遍历的字符数量;
3、每次对比脏字表的时候,减少运算量。
回过头分析上面的XDMP算法,是:
1、一次扫描;(很好,没啥好说的)
2、只要发现“起始符”就触发检索;
3、检索的时候,需要遍历的字符数是 1+2+3+...+n,这里的n是被命中的脏词的长度,或者最接近的长度;
4、每次检索,需要重复计算HashCode,不要忘了,计算HashCode,也是需要扫描字符串的,也就是又要遍历1+2+3+..+n个字符。
于是,我就有了一下问题:
1、难道每次遇到“起始符”了,就一定要触发检索吗?哎呀妈呀,这个也要检索(因为脏字表里面可能有MB)?!
2、难道每次触发检索,都非得要检索长度为1的,长度为2的,长度为3的……直到检索成功,或者出现非脏字表字符的时候吗?
3、难道每次检索,我们都需要把特定长度的待检文本截取出来吗?
4、难道每次检索,都需要从头开始计算哈希值吗?不能利用同一次触发检索后,上一次检索的哈希值,来减少本次计算的不必要运算量吗?
这四个问题,基本上是我想要解决的问题。其中前两个是一类问题,后两个是另一类问题。首先我们检查第一类问题:
好,我们回顾一下最开始的那篇英文,我们是否有点什么启发?对!我们触发检索的条件太简单了!
如果一个单词我们都没有看完呢,为什么要开始想这个事一个什么词呢?
另外,我们触发检索之后,也作了很多不必要的检索,因为当我们遇到"cao"这个字符的时候,很可能脏字表里面只有"caoT妈","caoN妈"这两种情况。如果有文章里面是"操作",脏字表里面正好又有"作LOVE",上述XDMP算法还是会乖乖的搜索两个字符的情况,而实际上又是没有必要的。
那么我们如何减少这些不必要的运算呢?首先,我们改一下,不要每次遇到“起始符”就触发检索。我们扫描到起始符怎么办?记录下来他的位置等信息,然后继续扫描下去。当我们遇到了“结束符”,也就是脏字表每一个词条中,最后一个字符中的任意一个时,我们才考虑是否要开始触发扫描。而扫描的时候呢,也不一定非得要脏字长度为1、2、3……的情况。因为之前记录了各种起始位置,我们可能只需要扫描1、3两种情况,或者5这种情况。
接下来是第二类问题:
上述算法里面,为了加快检索某串字符是否在脏字表里面,使用了哈希表。为了能够查表,所以就必须把这个哈希值给截取出来。可是这就引发了两个性能损耗点:
1、每一次截取,都要重新计算哈细值;
2、每一次都需要截取出一个字符串。
要避免这个问题,首先我们需要了解哈希表大致是怎么工作的:
哈希表实际上是根据当前的字符串内容,得出一个概率相对比较平均的散列值(这样哈希效表才不会容易出现冲突,即内容不同数值却一样),然后找出表中哈希值相等的第一个结果,然后对内容进行比较,如果相同就是找到了。否则就找下一个,直到没有相等哈希值的条目为止。
于是,我们可以这么来解决上述问题:
1、首先,我们造一个哈希值的计算方法,使得我们可以利用上一次的计算结果,接着计算下一个结果。
比如说,我们可以一个字节一个字节的进行异或(好处是方向性不敏感),或者也可以规定从字符串后方往前开始计算。
为什么规定从尾部进行计算?因为TTMP是结束符触发扫描的,比如说有文本:
ABCDE
如果E是结束符,那么就会检索ABCDE、BCDE、CDE、DE、E(还要看是否扫描到这些起始符)。如果我们是从后方往前计算,那就可以利用E的哈希值以及字符D,就可以计算DE的哈希值,而不需要再次对E字符进行计算了。
2、其次,我们可以构造这样的哈希表:
Dictionary
其key就是我们刚才算出来的哈希值,根据算出来的哈希值,我们就可以得到一个该哈希值下的脏字列表,然后我们一个个的和待检文本进行字符对字符的比较。这里看起来很奇怪,为什么有了哈希值,还不能够通过哈希值直接找到对应的字符呢?
不要忘了,哈希值本来就是会冲突的,我现在只不过把冲突的情况单独取出来自行处理,这样实际上的检索次数并没有增加(放在哈希表里面,也必须一个个的进行字符对字符的比较,才能够确定Key值是否完全相等,而不是Key的哈希值相等但Key值不等)。而好处是,我们不需要非得取出一个字符串,好让哈希表去获取这个字符串的哈希值(需要从头遍历每一个字符)。
通过以上的措施,我们就可以让每一次对n长度待检文本触发检索,只需要最多遍历n个字符,就可以得到最多n次遍历的所有哈希值了,而原XDMP算法则需要遍历Sum(n)个字符。
当然了,上述这几个措施,其效果并不会非常明显,原因有三个:
1、通常我们的文本都是很正常的文本,顶多偶尔有点敏感词汇,因此并不会经常挑战前面说到的性能损耗点;
2、通常我们的脏字表数量不会极其巨大,起始符和结束符也应该集中在有限的那些字符里面,因此绝大多数时候首字符表,以及结束符表就已经能够极大地提高性能了;
3、即使我们真的需要触发检索了,我们的脏字通常长度会比较短,或者大多数会比较短,因此上面的改进所带来的性能提升会比较有限。比如说两个字符的情况下,原算法计算哈希值需要遍历3个字符,而TTMP则只需要遍历2个字符……汗
而如果是5个字符,原算法需要遍历15个字符,而TTMP则只需要遍历5个字符,开始有差距感了。
可惜的是,5个字符的敏感词毕竟还是比较少的,而一篇文章正好中这个5字敏感词的地方也是很少的。
目前我这个TTMP算法还没有优化,已经能够做到和XDMP算法消耗时间比为1:1.5-2.5,算是很不错了。当然了XingD后来又做了一个新的算法,测试速度很快,可是当时我测的时候还不稳定,有漏检的情况,因此暂时不做评论了。
至于我的TTMP算法,也还有不少可以挖掘潜力的地方,比如现在是前向检索的,以及预先计算哈希值的。如果改成后向检索,检索时计算哈希值,性能应该会更好一点。不过暂时不打算继续挖掘了,准备把他先放到实战里面应用再说。
呃,其实本文开头说的还是没错的,本文还是有点难度,而本人描述能力也不是特别好,不知道各位看官有没有看懂了?
源码?嘿嘿,私货,先收藏一段时间再说。当然了,如果你有一段源码,能够合法制造让制造者合法拥有的人民币真币,能够用VS2005编译通过,部署过程只需要点一下鼠标,运行过程无需看管,并且你愿意和我交换的话,我会考虑一下的……真实的情况是,我现在还要继续让算法更稳定,不能放出一个问题多多的代码出来吧?
私下说一下,这个程序比XDMS算法复杂不少,如果将来放出来,并且各位想要整明白的话,还需要自己花点心思。
哦,顺预先给某人回复一下:
KMP算法是单模匹配算法,BM据说也是单模式的算法。
WM算法是多模匹配的,我找了一个据说是WM的算法看了看:
http://blog.chinaunix.net/u/21158/showart_228430.html
不知道你说的是不是这个。
我发现思路其实和KMP/BM类似,主要是通过“跳跃”技术来提升性能的。但是该文里面也提到了这么一段话:
假设其中一个模式非常的短,长度仅为2,那我们移动的距离就不可能超过2,所以短模式会使算法的效率降低。
可问题就在于,一般脏字表的长度都是1到2个的居多,因此绝大多数跳跃的作用并不强。即使是5个字符,再TTMP里面,也很可能因为超出长度没有遇到“结束符”而不会触发扫描。而WM需要有一个Shift表,为了节省空间还需要压缩,这就意味着需要对每一个扫描单元进行一个压缩计算。综上所述,TTMP和WM进行搜索脏字任务的PK,谁胜谁负还不一定呢。顺便说一下,即使是WM,也不是一次扫描的,因为如果不跳跃的话,就会要多扫描一下某些字符。
TTMP效率描述:
Ot = Ot(文本长度) + Ot[ 起始符与结束符在出现在扫描窗口中的次数*Avg(同一个结束符中哈希值相等的词条数目) ]
=Ot(N) + Ot[f*Avg(h)]
Om = Om(字符类型表) + Om(结束符表) + Om{ 词条总数*[哈希表内部变量消耗内存+列表消耗内存数量+Avg(词条长度) ] }
=256K + 256K + Om{n * [12+12+Avg(k) ] }
=512K + Om[n*(c+k)]
^_^ 唐僧回来了……