暑假总结
暑假总结
- 学到的新知识
- 差分约束
- tarjan与无向图
- 二分图
- 概率与数学期望
- 基环树
- 对几次考试的总结
- 对这次暑假补课的看法
学到的新知识
差分约束
给定n个变量和m个不等式,每个不等式形如 x[i] - x[j] <= a[k] (0 <= i, j < n, 0 <= k < m, a[k]已知),求 x[n-1] - x[0] 的最大值。例如当n = 4,m = 5,不等式组如图一-1-1所示的情况,求x3 - x0的最大值。
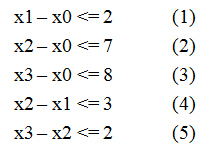
若题目中说要求最小的话,那么我们要跑最长路;若求最大的,那么我们要跑最短路。这里大体说下:就是求最小时,我们跑最长路,假如跑完后还有更小的,那么在跑最长路时一定还会对其进行松弛,使其变得更大,所以我们跑完最长路后,一定不会还存在更小的了。求最大的也同样的道理。
tarjan与无向图
https://www.luogu.org/problemnew/show/P3388
P3388 【模板】割点(割顶)
#include
#include
#include
#include
#include
#include
#include
#include
#define ll long long
using namespace std;
const int q=1000010;
struct node
{
int next,to;
}p[q*4];
int h[q],cnt=1;
void add(int a,int b)
{
++cnt;
p[cnt].next=h[a];
p[cnt].to=b;
h[a]=cnt;
}
int dfn[q],low[q],belong[q];
int stack[q],top=0,vistime=0,root=0;
vector dcc[q];
int num=0,gedian[q];
void tarjian(int x)
{
++vistime;
dfn[x]=low[x]=vistime;
stack[++top]=x;
if(root==x&&h[x]==0)
{
dcc[++num].push_back(x);
return;
}
int flag=0;
for(int i=h[x];i;i=p[i].next)
{
int u=p[i].to;
if(!dfn[u])
{
tarjian(u);low[x]=min(low[x],low[u]);
if(low[u]>=dfn[x])
{
flag++;
if(x!=root||flag>1) gedian[x]=1;
num++;
int y;
do
{
y=stack[--top];
dcc[num].push_back(y);
}while(y!=u);
dcc[num].push_back(x);
}
}
else low[x]=min(low[x],dfn[u]);
}
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);add(y,x);
}
for(int i=1;i<=n;++i)
if(!dfn[i]) {root=i;tarjian(i);}
int sum=0;
for(int i=1;i<=n;++i)
if(gedian[i]) ++sum;
printf("%d\n",sum);
for(int i=1;i<=n;++i)
if(gedian[i]) printf("%d\n",i);
}
https://www.luogu.org/problemnew/show/P2860
P2860 [USACO06JAN]冗余路径Redundant Paths
直接统计度,计算能得54分
缩点后统计度,计算能AC
我不知道为什么直接统计不能得满,我是看了算法标签有缩点后,尝试缩点过的。
#include
#include
#include
#include
#include
#include
#include
#define ll long long
using namespace std;
const int q=1000010;
struct node
{
int next,to,from;
}p[q*4],p1[4*q];
int h[q],cnt=1;
void add(int a,int b)
{
++cnt;
p[cnt].next=h[a];
p[cnt].to=b;
p[cnt].from=a;
h[a]=cnt;
}
int h1[q],cnt1=0;
void add1(int a,int b)
{
++cnt1;
p1[cnt1].next=h1[a];
p1[cnt1].to=b;
p1[cnt1].from=a;
h1[a]=cnt;
}
int dfn[q],low[q],vistime=0,bridge[q];
void tarjian(int x,int bian)
{
++vistime;
dfn[x]=low[x]=vistime;
for(int i=h[x];i;i=p[i].next)
{
int u=p[i].to;
if(!dfn[u])
{
tarjian(u,i);
low[x]=min(low[x],low[u]);
if(low[u]>dfn[x])bridge[i]=bridge[i^1]=1;
}
else if(i!=(bian^1)) low[x]=min(low[x],dfn[u]);
}
}
int c[q],dcc=0,deg[q];
void dfs(int x)
{
c[x]=dcc;
for(int i=h[x];i;i=p[i].next)
{
int u=p[i].to;
if(c[u]||bridge[i]) continue;
dfs(u);
}
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
}
/* if(n==16&&m==22)
{
printf("3");
return 0;
}*/
for(int i=1;i<=n;++i)
if(!dfn[i]) tarjian(i,0);
/*for(int i=2;i<=cnt;++i)
if(bridge[i])
printf("%d %d\n",p[i].from,p[i].to);*/
for(int i=1;i<=n;++i)
if(!c[i])
{
++dcc;
dfs(i);
}
//printf("%d\n",dcc);
for(int i=2;i<=cnt;++i)
{
int x=p[i].from,y=p[i].to;
if(c[x]==c[y]) continue;
//add1(c[x],c[y]);
++deg[c[x]];
//printf("%d %d\n",c[x],c[y]);
}
int sum=0;
for(int i=1;i<=dcc;++i)
if(deg[i]==1) ++sum;
printf("%d",(sum+1)/2);
}
二分图
https://www.luogu.org/problemnew/show/P1525
P1525 关押罪犯
我做的时候用的并查集,所以就不放代码了。
概率与数学期望
1.条件概率:设A、B是两个事件,且P(B)>0,则在事件B发生的条件下,事件
A发生的概率为:P(A|B)=P(AB)/P(B)。其中P(AB)表示A和B同时发生的概率,
可理解为交集。
2.乘法公式:条件概率的变形和扩展
(1) P(AB)=P(B)*P(A|B)= P(A) *P(B|A)
(2)P(A1A2…An-1An)=P(A1)*P(A2|A1)P(A3|A1A2)…*P(An|A1A2…An-1)
3.全概率公式
基环树
基环树找环
void dfs(int u) //基环树找出基环上的所有点
{
vis[u] = ++vs;//时间戳
for (int i = h[u]; i; i = edg[i].next)
{
int v = edg[i].to;
if (v == fa[u]) continue;
if (vis[v])
{
if (vis[v] < vis[u]) continue;
ans[++tot] = v;
for ( ; v != u; v = fa[v]) ans[++tot] = fa[v];
}
else fa[v] = u, dfs(v);
}
}
基环树的题基本都是断边。
对几次考试的总结
总体来说考的一般。
具体的总结基本都整理过了,就不复制过来了。
对这次暑假补课的看法

之前的课上的很碎,没有整块整块的时间。
而且有的知识点都没有时间做题,东西基本学过就忘。
经过暑假的集训,对之前学习的知识有了更好的理解。
也能更好的用,也对模板更加熟悉。
每天都要自我催眠,我爱编程,我爱学习。
这个暑假总体来说还是学习到挺多的东西的。