数据结构与算法_线性表、栈、队列习题

线性表、栈、队列习题

905.按奇偶排序数组
给定一个非负整数数组 A，返回一个数组，在该数组中， A 的所有偶数元素之后跟着所有奇数元素。
你可以返回满足此条件的任何数组作为答案。

示例：
输入：[3,1,2,4]
输出：[2,4,3,1]
输出 [4,2,3,1]，[2,4,1,3] 和 [4,2,1,3] 也会被接受。
提示：

1. 1 <= A.length <= 5000
2. 0 <= A[i] <= 5000

public int[] sortArrayByParity(int[] A) {
        /**
         * 解法1：头尾交换O(n)
         * 任何传进的参数都有特殊情况
         * 在没有参数说明之前 最好进行判断
         * 左偶右奇 L++ R--
         * 左偶右偶 L++
         * 左奇右奇 R--
         * 左奇右偶 交换
        if(A==null||A.length==1||A.length==0){
			return A;
		}
		int L=0;
		int R=A.length-1;
		while(L
		
		/**
		 * 解法2：不改变原先数字的相对顺序
		 * =>[1,2,3,4,5,6]
		 *   [2,4,6,1,3,5]=>
		 * 冒泡排序O(n^2) 
		 * 选择排序O(n^2) 
		 * 插入排序O(n^2) √ 是保证相对顺序的
		 * */
		int e=0;
		int j=0;
		for(int i=1;i<A.length;i++){
			if(A[i]%2==1){
				continue;
			}
			e=A[i];
			for(j=i;j>0&&A[j-1]%2==1;j--){
				A[j]=A[j-1];
			}
			A[j]=e;
		}
		return A;
    }

解题思路：

1. 前后交换，定义两个指针(L,R)，一个从前往后(L)，另一个从后往前®。如果前边为偶数，后边为奇数，则L++,R–；如果前边为偶数后边为奇数，则L++；如果前边为奇数，后边为奇数，则R–；如果前边为奇数后边为偶数，则交换两个数。
2. 用插入排序，保证数组的相对顺序不变。遍历数组，从前往后，如果是奇数，则跳出本次循环；如果是偶数，依次往前移。

169.求众数
给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2

public int majorityElement(int[] nums) {
		/**
		 * 解法1：连续相等数字个数+滑窗思想
		   前提需要排序
		Arrays.sort(nums);
		int count=0;
		int aim=0;
		int curCount=0;
		int curAim=0;
		int j=0;
		for(int i=0;i(nums.length-1)/2){
				break;
			}
			curAim=nums[i];
			curCount=1;
			for(j=i+1;jcount){
				count=curCount;
				aim=curAim;
			}
			i=j;
		}
		return aim;
		 * */
		
		/**
		 * 解法2：消除
		 * 
		 * */
		int num=nums[0];
		int count=1;
		for(int i=1;i<nums.length;i++){
			if(nums[i]==num){
				count++;
			}else{
				count--;
				if(count==0){
					num=nums[i];
					count=1;
				}
			}
		}
		return num;
	}

解题思路：

1. 先排序，在定义变量记录元素和元素出现的次数，如果后面元素出现的次数大于前面的，覆盖掉前面的元素和次数，最终得到的元素为结果。
2. 定义一个变量num记录为数组的第一个元素，再定义一个变量count记录次数，从第二个元素遍历数组，如果等于num即count++，否则count–，当count==0，则将第i个元素赋给num，最后得到的num为程序结果。

118. 杨辉三角
给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。
在杨辉三角中，每个数是它左上方和右上方的数的和。
示例:

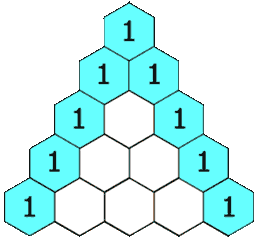
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]

public List<List<Integer>> generate(int numRows) {

		List<List<Integer>> lists = new ArrayList<List<Integer>>();

		for (int i = 1; i <= numRows; i++) {
			
			ArrayList<Integer> list = new ArrayList<Integer>();

			for (int j = 0; j < i; j++) {
				if (j == 0 || j == i - 1) {
					list.add(1);
				} else {
					list.add(lists.get(i - 2).get(j) + lists.get(i - 2).get(j - 1));
				}
			}
			lists.add(list);
		}
		return lists;
	}

解题思路：

先创建一个线性表lists使其长度等于传进来的数值，再循环添加线性表list到lists中，当list的索引为0或者上一个线性表的长度时，给list里面添加1，否则，将与当前索引对应的上一次的索引值和上一次索引减一的值相加赋予当前索引。返回的lists即程序结果。

766.托普利茨矩阵
如果一个矩阵的每一方向由左上到右下的对角线上具有相同元素，那么这个矩阵是托普利茨矩阵。
给定一个 M x N 的矩阵，当且仅当它是托普利茨矩阵时返回 True。

示例 1:
输入:
matrix = [
[1,2,3,4],
[5,1,2,3],
[9,5,1,2]
]
输出: True
解释:
在上述矩阵中, 其对角线为:
“[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”。
各条对角线上的所有元素均相同, 因此答案是True。
示例 2:
输入:
matrix = [
[1,2],
[2,2]
]
输出: False
解释:
对角线"[1, 2]"上的元素不同。

说明:

1. matrix 是一个包含整数的二维数组。
2. matrix 的行数和列数均在 [1, 20]范围内。
3. matrix[i][j] 包含的整数在 [0, 99]范围内。

public boolean isToeplitzMatrix(int[][] matrix) {
		int row = matrix.length;
		int col = matrix[0].length;

		//1.列方向几个头
		for (int i = 0; i < col - 1; i++) {
			int x = 1;
			int y = i + 1;
			while (x >= 0 && x < row && y >= 0 && y < col) {
				if (matrix[x][y] != matrix[0][i]) {
					return false;
				}
				x++;
				y++;
			}
		}
		//2.行方向几个头
		for (int i = 1; i < row - 1; i++) {
			int x = i + 1;
			int y = 1;
			while (x >= 0 && x < row && y >= 0 && y < col) {
				if (matrix[x][y] != matrix[i][0]) {
					return false;
				}
				x++;
				y++;
			}
		}
		return true;
	}

解题思路：

首先，按行去遍历，从第一个行的第一个元素到行长度减一的元素，依次与斜下角的元素相比较，如果有一个不等，返回false;然后从第二行的第一列为头遍历，与上次雷同遍历到列的长度减一，如果有一个不等，返回false；如果都不返回false，则返回true。

1013.将数组分成和相等的三部分
给定一个整数数组 A，只有我们可以将其划分为三个和相等的非空部分时才返回 true，否则返回 false。

形式上，如果我们可以找出索引 i+1 < j 且满足 (A[0] + A[1] + … + A[i] = = A[i+1] + A[i+2] + … + A[j-1] == A[j] + A[j-1] + … + A[A.length - 1]) 就可以将数组三等分。

示例 1：
输出：[0,2,1,-6,6,-7,9,1,2,0,1]
输出：true
解释：0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
示例 2：
输入：[0,2,1,-6,6,7,9,-1,2,0,1]
输出：false
示例 3：
输入：[3,3,6,5,-2,2,5,1,-9,4]
输出：true
解释：3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4

public boolean canThreePartsEqualSum(int[] A) {

		int sum = 0;
		for (int num : A) {
			sum += num;
		}
		int key = sum / 3;
		int temp = 0;
		for (int i = 0; i < A.length; i++) {
			key = key - A[i];
			if (key == 0) {
				temp++;
				key = sum / 3;
			}
		}
		return temp == 3;
	}

解题思路：
先计算数组中所有元素的和sum，依题意是相等的三部分，key=sum/3为每一部分的和。定义一个计数器temp=0。循环遍历数组，用kay的值减去每次遍历的值，当sum/3等于0时，temp++,再将sum/3赋予key；遍历完成后返回temp是否等于3，即程序结果。

167.两数之和|| - 输入有序数组
给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:
返回的下标值（index1 和 index2）不是从零开始的。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

public int[] twoSum(int[] numbers, int target) {
       
		for (int i = 0; i < numbers.length; i++) {
			int index = binarySearch(numbers, i + 1, numbers.length-1, target - numbers[i]);
			if (index != -1) {
				return new int[] { i + 1, index + 1 };
			}
		}
		return null;

	}

	public int binarySearch(int[] arr, int begin, int end, int key) {
		int min = begin;
		int max = end;
		int mid = (min + max) / 2;
		while (arr[mid] != key) {
			if (arr[mid] > key) {
				max = mid - 1;
			} else if (arr[mid] < key) {
				min = mid + 1;
			}
			if (min > max) {
				return -1;
			}
			mid = (min + max) / 2;
		}
		return mid;
	}

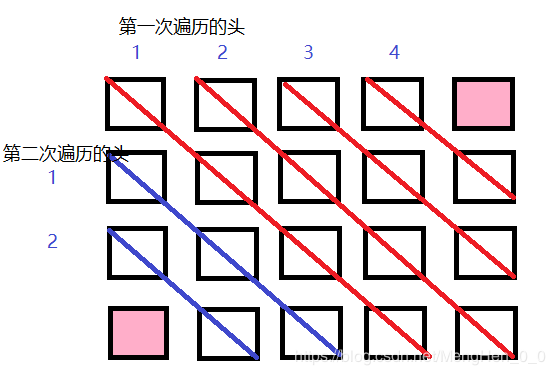
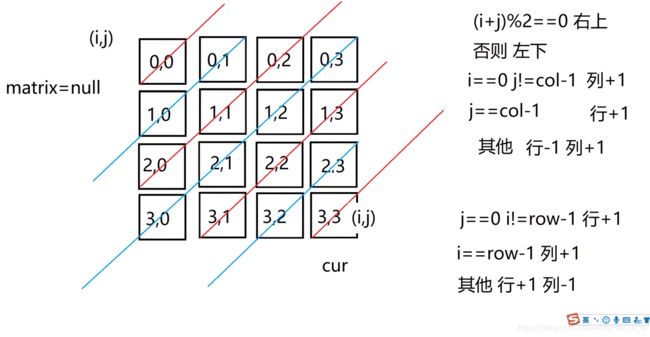
498.对角线遍历
给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

示例:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,4,7,5,3,6,8,9]
解释:
说明:

1. 给定矩阵中的元素总数不会超过 100000 。

public int[] findDiagonalOrder(int[][] matrix) {
		/*
		 * matrix==null 连个鸡毛都没有 matrix.length 有数组但一个元素都没有 col==0 有行 但是每行没元素
		 * row==1 只有一行(不管没有元素) col==1 只有一列(多个行 每行只有一个元素)
		 */
		if (matrix == null || matrix.length == 0) {
			return new int[] {};
		}
		int row = matrix.length;
		int col = matrix[0].length;

		// {{},{},{},{},{}}
		if (col == 0) {
			return new int[] {};
		}
		// 二维数组只有一行
		if (row == 1) {
			return matrix[0];
		}
		// 二维数组只有一列
		int[] nums = new int[row * col];
		if (col == 1) {
			for (int i = 0; i < row; i++) {
				nums[i] = matrix[i][0];
			}
			return nums;
		}

		int i = 0;
		int j = 0;
		int index = 0;
		while (i < row && j < col) {
			// 读取(i,j)元素
			nums[index++] = matrix[i][j];
			if ((i + j) % 2 == 0) {// 右上
				if (i == 0 && j != col - 1) {
					j++;
				} else if (j == col - 1) {
					i++;
				} else {
					i--;
					j++;
				}
			} else {// 左下
				if (j == 0 && i != row - 1) {
					i++;
				} else if (i == row - 1) {
					j++;
				} else {
					i++;
					j--;
				}
			}
		}
		return nums;
	}

解题思路：

如图，当（i+j）%2==0时，朝右上遍历；否则，左下遍历。
当i= =0并且j!=col-1时，列+1；当j= = col-1时，行+1；其他行-1，列+1。
当j= =0并且i!=row-1时，行+1；当i= = col-1时，列+1；其他行+1，列-1。

724.寻找数组的中心索引
给定一个整数类型的数组 nums，请编写一个能够返回数组“中心索引”的方法。
我们是这样定义数组中心索引的：数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
如果数组不存在中心索引，那么我们应该返回 -1。如果数组有多个中心索引，那么我们应该返回最靠近左边的那一个。

示例 1:
输入:
nums = [1, 7, 3, 6, 5, 6]
输出: 3
解释:
索引3 (nums[3] = 6) 的左侧数之和(1 + 7 + 3 = 11)，与右侧数之和(5 + 6 = 11)相等。
同时, 3 也是第一个符合要求的中心索引。
示例 2:
输入:
nums = [1, 2, 3]
输出: -1
解释:
数组中不存在满足此条件的中心索引。
说明:
nums 的长度范围为 [0, 10000]。
任何一个 nums[i] 将会是一个范围在 [-1000, 1000]的整数。

public int pivotIndex(int[] nums) {
        if(nums==null){
        	return -1;
        }
        int sum=0;
        int leftSum=0;
        int rightSum=0;
        for(int num:nums){
        	sum+=num;
        }
        for(int i=0;i<nums.length;i++){
        	if(i==0){
        		leftSum=0;
        	}else{
        		leftSum+=nums[i-1];
        	}
        	rightSum=sum-leftSum-nums[i];
        	if(leftSum==rightSum){
        		return i;
        	}
        }
        return -1;
    }

解题思路：
计算数组的个元素和为sum，再定义左边和及右边和，遍历元素，遍历一个左边加一个（leftSum+=nums[i+1])，再用sum-leftSum得到rightSum,当leftSum==rightSum时，返回i即为程序结果。