数据描述性分析

统计分析分为统计描述和统计推断。统计描述是通过绘制统计图、编制统计表、计算统计量等方法来描述数据的分布特征。它是数据分析的基本步骤，也是统计推断的基础。

一.描述统计量

已知一组试验（或观测）数据为，它可以是从所要研究的对象的总体X中取出的，这n个观测值就构成了一个样本。在某些简单的实际问题中，这n个观测值就是所要研究问题的全体。数据分析的任务是要对这全部n个数据进行分析，提取数据中包含的有用信息。

分析数据的主要特征，要研究数据的数字特征：数据的集中位置、分散程度和数据分布等。

1.位置的度量

位置的度量是用来描述数据的集中趋势的统计量。常用的有：均值、众数、中位数、百分位数等。

（1）均值

均值，平均数，R中求均值的函数为mean()，其使用形式为：

mean(x, trim = 0, na.rm = FALSE, ...)

其中，x是对象（向量、矩阵、数组或数据框），trim是计算均值前去掉与均值差较大数据的比例，缺省为0，即包含全部数据。当na.rm = TRUE时，允许数据中有缺失数据。

例：

已知12位同学的体重（kg）为：57 64 41 38 35 44 41 51 57 49 47 46，求均值。

>w<-c(57,64,41,38,35,44,41,51,57,49,47,46)

> mean(w)

[1] 47.5

计算结果为体重均值为47.5.

注意：当x为矩阵（或数组）时，函数mean()的返回值是矩阵中全部数据的平均值。

如：

> x<-1:12

> dim(x)<-c(3,4)

> mean(x)

[1] 6.5

与mean(1:12)的返回值相同，而这里x是一个3*4的矩阵。

如果计算矩阵各行各列的矩阵，需要调用前一课中的apply()函数。

计算矩阵各行的均值：

> apply(x,1,mean)

[1] 5.5 6.5 7.5

计算矩阵各列的均值：

> apply(x,2,mean)

[1] 2  5  8 11

多元数据的输入最好采用数据框的形式，这样便于后面的数据处理。

与均值函数mean()相关的函数还有weighted.mean()，即计算数据的加权平均值。使用格式为：weighted.mean(x, w, na.rm = FALSE...)

其中x是数值向量，w是数据x 的权重，与x的维数相同，na.rm意义与mean()中相同。

 

（2）顺序统计量

sort()函数可给出顺序统计量，如：

> sort(w)

 [1]35 38 41 41 44 46 47 49 51 57 57 64

sort()的使用格式：

sort.int(x, partial = NULL, na.last = NA,decreasing = FALSE,

        method = c("shell", "quick"), index.return = FALSE)

其中x是向量（数值、字符、逻辑）。Partial是部分排序的指标向量。na.last是控制缺失数据的参数，当na.last=NA，不处理缺失数据；当na.last=T，缺失数据排最后；当na.last=F，缺失数据排最前。decreasing是逻辑变量，当decreasing=F（缺省），则从小到大排；当decreasing=T时，从大到小排。method是排序方法，缺省为shell，quick是快速排序法，对于数值型向量，快速排序法的运算量低于shell的运算量。index.return是逻辑变量，控制排序下标的返回值，当index.return=T（缺省为F）时，返回值是一个列表，列表一个变量$x是排序的顺序，第二个变量是$ix是排序顺序的下标对应的值。

> sort(w,decreasing=T)

 [1]64 57 57 51 49 47 46 44 41 41 38 35

> sort(w,decreasing=T,index.return = T)

$x

 [1]64 57 57 51 49 47 46 44 41 41 38 35

 

$ix

 [1] 2  1  9  8 1011 12  6 3  7  4  5

 

（3）中位数

中位数为数据排序中位于中间位置的值，当数据个数为奇数时，中位数为中间位置的值，当数据个数为偶数时，中位数为中间两个值得平均。

中位数描述数据中心位置的数字特征。大体上比中位数大或小的数据个数为整个数据的一半。对于对称分布的数据，均值与中位数比较接近；对于偏态分布的数据，均值与中位数不同。中位数的又一显著特点是不受异常值的影响，具有稳健性，因此它是数据分析中相当重要的统计量。

R中计算中位数的函数为median()，如：

> median(w)

[1] 46.5

使用格式为median(x, na.rm = FALSE)，参数含义与mean()相同。

 

（4）百分位数

百分位数是中位数的推广。将数据按从小到大的排列后，对于，它的p分位点定义为：当np不是整数时，；当np是整数时，。表示np的整数部分。

P分位数又称为第100p百分位数。如0.5分位数（第50百分位数）就是中位数。实际中，0.75分位数与0.25分位数（第75百分位数与第25百分位数）比较重要，它们分别称为上、下四分位数，记为，。

R中，quantile()函数用来计算观测值的百分位数，如：

> quantile(w)

 0%  25%  50% 75%  100%

35.0  41.0  46.5 52.5  64.0

quantile()函数的一般使用格式为：

quantile(x, probs = seq(0, 1, 0.25), na.rm= FALSE, ...)

其中，x是数值向量，probs是给出相应的百分位数，缺省为0,0.25,0.5,0.75,1，na.rm是否有缺失值。

如果给出0,20%，40%，60%，80%，100%的百分位数，则选择：

> quantile(w,probs=seq(0,1,0.2))

 0%  20%  40% 60%  80% 100%

35.0 41.0 44.8 48.2 55.8 64.0

 

2.分散程度的度量

表示数据分散（或变异）程度的数字特征有方差、标准差、极差、四分卫极差和标准误等。

（1）方差、标准差

样本方差是样本相对于均值的偏差平方和的平均（除以n-1），样本方差的开方为样本标准差。

R中，var()函数计算样本方差，sd()计算样本标准差。

> var(w)

[1] 73.90909

> sd(w)

[1] 8.59704

与方差相关的函数还有：cov()求协方差矩阵，cor()求相关系数矩阵。

 

（2）极差与标准误

样本极差是样本最大值与最小值之差。当数据越分散，极差越大。

四分卫差（半极差）是样本上、下四分位数之差。它也是度量样本分散性的数字他正，特备对于具有异常值的数据，它作为分散性具有稳健性，因此它在稳健性数据分析中有重要作用。

样本标准误：，即标准差除以样本个数的开方

3.分布形状的度量

（1）峰度系数

，其中，s是标准差，是样本3阶中心矩，即。

偏度系数的刻画数据的对称性的指标。关于均值对称的数据其偏度系数为0，右侧又分散的数据偏度系数为正，左侧更分散的数据偏度系数为负。

 

（2）偏度系数

其中，s是标准差，是样本4阶中心矩，即。

当数据的总体分布为正态分布时，峰度系数近似为0；当分布较正态分布的尾部更分散时，峰度系数为正；否则为负。当峰度系数为正时，两侧极端数据较多；当峰度系数为负时，两侧极端数据较少。

 

二.数据的分布

数据的数字特征刻画了数据的主要特征，而要对数据的总体情况作全面的描述，就要研究数据的分布。对数据分布的主要描述方法有直方图、茎叶图和数据理论分布即总体分布。数据分析的一个重要问题是要研究数据是否来自正态总体，这是分布的正态性检验的问题。

1.分布函数

R中，提供了计算这些典型分布的分布函数、分布律或概率密度函数，以及分布函数的反函数的各种函数。

正态分布函数dnorm(x, mean = 0, sd = 1, log = FALSE)

正态概率密度函数pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)

正态分布下分位点函数qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)

生成正态分布随机数函数rnorm(n, mean = 0, sd = 1)

其中，x、q是数值型变量构成的向量。P是由概率构成的向量。N是产生随机数的个数。mean是要计算的正态分布的均值，缺省为0。sd是要计算的正态分布的标准差，缺省为1。log、log.p是逻辑变量，当它为T时，函数返回值不是正态分布，而是对数正态分布。lower.tail是逻辑变量，当它是T（缺省）时，，当它是F时，。

其他的分布类似，常用的函数如下：

 

2.直方图、经验分布与QQ图

（1）直方图

对于数据分布，常用直方图（histgram）进行描述。将数据取值的范围分成若干区间（一般是等间隔的），在等间隔的情况下，每个区间长度称为组距。考察数据落入每一区间的频数与频率，在每个区间上画一个矩形，它的宽度是组距，高度可以是频数、频率或频率/组距，在高度是频率/组距的情况下，每一矩形的面积恰是数据落入区间的频率，则中直方图可以估计总体的概率密度。组距对直方图的形态有很大的影响，组距太小，每组的频数较少，由于随机性的影响，临近区间的频数可能很大；组距太大，直方图所反映的形态就不灵敏。

R中，用hist()函数画出样本的直方图，格式为：

hist(x)

或

hist(x, breaks = "Sturges",

    freq = NULL, col = NULL,

    main = paste("Histogram of" , xname),

    xlim = range(breaks), ylim = NULL,

    xlab = xname, ylab, ...)

其中，x是样本构成的向量。breaks规定直方图的组距。由以下几种形式给出：向量（给出直方图的起点、终点与组距）、数（定义直方图的组距）、字符串（见缺省状态）、函数（计算组距的宽度）。freq是逻辑变量，当freq=T时绘制频率直方图，当freq=F绘制密度直方图。main是指直方图的标题，xlim、ylim分别为x、y轴范围，xlab、ylab分别为x、y轴标签。更多参数设定参见?hist。

 

（2）核密度估计函数

与直方图配套的是核密度估计函数density()，其目的是用已知样本，估计其密度。它的使用方法，详细参数设定参见?density()。

 

例：w为之前体重的数据

> hist(w,freq=F)

> lines(density(w),col="blue")##lines()函数为在前一图中添加新图

> x<-35:65

>lines(x,dnorm(x,mean(w),sd(w)),col="red")

我们可以看到，密度估计曲线与正态分布的概率密度曲线还是有一定的差别的。

 

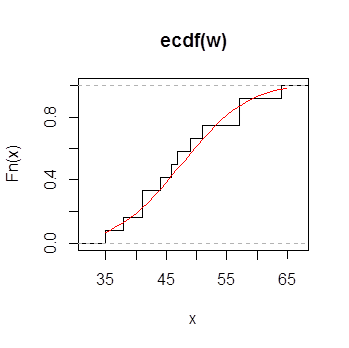
（3）经验分布

直方图的制作适合于总体为连续型分布的场合。若对于一般的总体分布，若要它的总体分布函数F(x)，可以用经验分布函数。

R中用ecdf()来绘制经验分布函数，用法是：

ecdf(x)

plot(x,ylab=”Fn(x)”,verticals=F,col.01line=”gray70”)

其中，函数ecdf()中的x是由观察值得到的数值型向量。函数plot()中的x是由ecdf()生成的向量。Verticals是逻辑变量，当verticals=T时表示画竖线，当verticals=F（缺省）时不画竖线。

例：

>plot(ecdf(w),verticals=TRUE,do.p=FALSE)

> x<-35:65

> lines(x,pnorm(x,mean(w),sd(w)),col="red")

其中do.p是逻辑变量，当do.p=F时表示点处不画记号，当do.p=T时表示点处画记号。

（4）QQ图

不论是直方图还是经验分布图，要从比较上鉴别样本是否近似于某种类型的分布是困难的。QQ图可以帮助我们鉴别样本的分布是否近似于某种类型的分布。

假定总体为正态分布，对于样本，其顺序统计量是。设是标准正态分布的分布函数，是反函数。正态分布的QQ图是由以下的点构成的散点图。若样本数据近似于正态分布，在QQ图上这些点近似地在直线附近。此直线的斜率是标准差，截距是均值。利用QQ图可以作直观的正态性检验。若QQ图上的点近似地在一条直线附件，可认为样本数据来自正态分布总体。

R中，函数qqnorm()和qqline()提供了画正态QQ图的方法。

qqnorm(y, ...)

qqline(y, datax = FALSE, distribution =qnorm,

      probs = c(0.25, 0.75), qtype = 7, ...)

其中，x是第一列样本，y是第二列样本。其他参数见帮助文件。

例：体重数据的例子

> qqnorm(w)

> qqline(w)

从QQ图来看，样本的数据基本上可以看成来自正态总体。对于对数正态、指数等也可以作相应的QQ图，用以鉴别样本数据是否来自某一类型的总体分布。

 

3.箱线图与五数总结

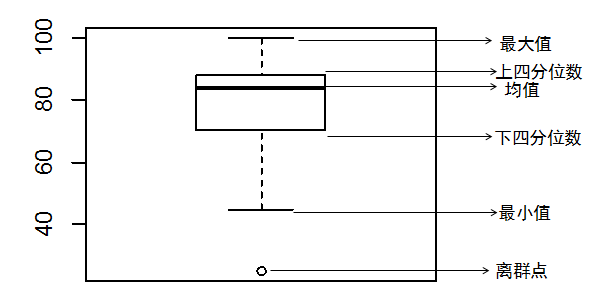
（1）箱线图

箱线图可以直观简洁得展现数据分布的主要特征。R中用boxplot()函数作箱线图。

例：某班学生31名的考试成绩如下：

>x<-c(25, 45, 50, 54, 55, 61, 64, 68,72, 75, 75, 78, 79, 81, 83, 84, 84, 84, 85, 86, 86, 86, 87, 89, 89, 89, 90, 91,91, 92, 100)

> boxplot(x)

boxplot()函数的详细用法见帮助文档。

 

（2）五数总结

在探索性数据分析中，认为最有代表性的、能反映数据重要特征的五个数：中位数，下四分位数、上四分位数、最小值、最大值。这五个数称为样本数据的五数总结。R中用fivenum()计算样本的五数总结。使用格式：

fivenum(x,na,rm=TURE)，其中参数设定同mean()。

 

4.正态性检验与分布拟合检验

前面介绍的图像生动直观，然而其中所配曲线是否合适，是需要进行统计检验的。

（1）正态性W检验方法

利用Shapiro-Wilk统计量作正态性检验。

函数：shapiro.test()，使用格式为shapiro.test(x)，其中x是向量，且向量长度在3到5000之间。

例：体重的例子

> shapiro.test(w)

 

       Shapiro-Wilk normality test

 

data: w

W = 0.9663, p-value = 0.8682

P值0.8682>0.05，因此，认为来自正态分布总体，与QQ图结论相同。

又如：

> shapiro.test(runif(100,min=2,max=4))

 

       Shapiro-Wilk normality test

 

data: runif(100, min = 2, max = 4)

W = 0.946, p-value = 0.0004593

其中，runif(100,min=2,max=4)是生成服从最小值2最大值4的均匀分布的100个随机数，这里的p值0.0004593<0.05，认为赝本不是来自正态分布的总体。

 

（2）经验分布的k-s检验方法

经验分布函数是总体分布函数的估计。经验分布拟合检验的方法是检验经验分布于假设的总体分布函数之间的差异。可使用Kolmogorov-Smirnov统计量来检验。

R中，ks.test()函数给出了Kolmogorov-Smirnov检验方法，使用方法是：

ks.test(x, y, ...,

       alternative = c("two.sided", "less","greater"),

       exact = NULL)

其中x是待检测的样本构成的向量，y是原假设的数据向量或是描述原假设的字符串。如：

> x<-rt(100,5)

> ks.test(x,"pf",2,5)

 

       One-sample Kolmogorov-Smirnov test

 

data: x

D = 0.52, p-value < 2.2e-16

alternative hypothesis: two-sided

其中，x是来自t分布的随机数，对x作F(2,5)检验（即认为是来自总体是自由度为（2,5）的F分布），其结果是p值< 0.05，拒绝原假设，即不认为x服从F(2,5)的分布。

参考：《统计建模与R软件》 薛毅 陈立萍 编著 清华大学出版社