高等数学：第八章 多元函数的微分法及其应用（8）多元函数极值及其求法

§8.8  多元函数极值及其求法

一、多元函数的极值

1、多元函数极值定义

设函数在点的某个邻域内有定义,对该邻域内异于的点,如果都适合不等式

则称函数在点取极大值；

如果都适合不等式

则称函数在点取极小值。

极大值与极小值统称为函数的极值；使函数取得极值的点称为极值点。

注:二元函数的极值是一个局部概念,这一概念很容易推广至元函数。

【例1】讨论下述函数在原点是否取得极值。

(1)、

(2)、

(3)、

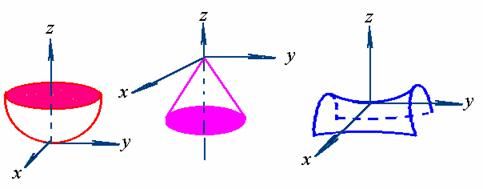
解:由它们的几何图形可知:

是开口向上的旋转抛物面,在取得极小值；

是开口向下的锥面,在取得极大值；

是马鞍面, 在不取得极值。

2、函数取得极值的必要条件

【定理一】设函数在点具有偏导数且取得极值,则它在该点的偏导数必为零,即

【证明】不妨设在点处有极大值。

依极值定义,点的某一邻域内的一切点适合不等式

特殊地,在该邻域内取,而的点,也应有不等式

这表明:一元函数在 处取得极大值,因而必有

同理可证

【注一】当时, 曲面在点处有切平面

此切平面平行于水平面面。

例如,在点取得极小值, 它在点处,

其切平面为

即        

此切平面就是(面)。

使同时成立的点,称为函数的驻点。

【注二】定理一表明,可(偏)导函数的极值点必为驻点,反过来,函数的驻点却不一定是极值点。例如,在点不取得极值,但却是驻点。这告诉我们,驻点仅仅是函数可疑的极值点,要判断它是否真为极值点,需要另作判定。

【注三】偏导数或不存在的点也是函数的可疑极值点。

例如,在点有极大值,但

 不存在。

当然,也不存在。

当然,定理一的结论也可推广至元函数。

3、函数取得极值的充分条件

【定理二】设函数在点的某邻域内连续,且有一阶及二阶连续的偏导数,又  ,记

 ,  ,

则函数在处是否取得极值的条件如下

(1)、时具有极值,且当时有极大值,

 当时有极小值；

(2)、时没有极值；

(3)、时可能有极值,也可能没有极值,需另作判定。

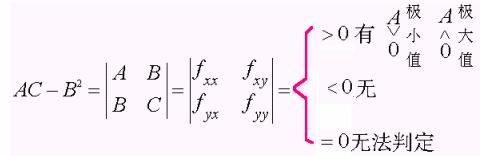
对这一定理不作证明,仅介绍它的记忆之法:

【例2】求函数的极值。

解:函数具有二阶连续偏导数, 故可疑的极值点只可能为驻点,

先解方程组

求出全部驻点为

再求二阶偏导数

在点处,

函数取得极小值 ；

在点处,

函数不取得极值；

在点处,

函数不取得极值；

在点处,

函数取得极大值  。

二、多元函数的最值

1、有界闭区域上连续函数的最值确定

如果二元函数在有界闭区域上连续,则在上必定取得最值。使函数取得最值的点既可能在的内部,也可能在的边界上。

若函数在的内部取得最值,那未这个最值也是函数的极值。而函数取得极值的点使的驻点或使、不存在的点。

若函数在的边界上取得最值,可根据的边界方程,将化成定义在某个闭区间上的一元函数,进而利用一元函数求最值的方法求出最值。

综合上述讨论,有界闭区域上的连续函数最值求法如下:

(1)、求出在的内部,使,同时为零的点及使或不存在的点；

(2)、计算出在的内部的所有可疑极值点处的函数值；

(3)、求出在的边界上的最值；

(4)、比较上述函数值的大小,最大者便是函数在上的最大值；最小者便是函数在上的最小值。

【例3】求二元函数在矩形区域

上的最值。

解:

得驻点,且

在边界 上,,

 且

在边界上,   , 则

在边界 上, , 则 ,

则  ；

在边界上,  , 因

, 故单调增加, 从而 。

比较上述讨论, 有

 为最大值,

 为最小值。

2、开区域上函数的最值确定

求函数在开区域上的最值十分复杂。

但是,当所遇到的实际问题, 据问题的性质可断定函数的最值一定在上取得,而函数在上又只有一个驻点, 那么就可以肯定该驻点处的函数值就是函数在上的最值。

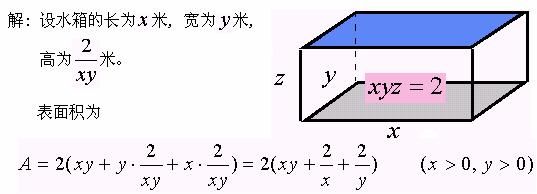
【例4】某厂要用铁板做成一个体积为立方米的有盖长方体水箱, 当长、宽、高各取怎样的尺寸时,才能用料最省?

令 

解方程组得唯一驻点 ,

据问题的实际背景, 水箱所用材料面积的最小值一定存在, 并在开区域内取得,又函数在内只有唯一的驻点, 因此, 可断定当 时, 取得最小值。

这表明: 当水箱的长、宽、高分别为米时, 所用材料最省, 此时的最小表面积为。

三、条件极值与拉格朗日乘数法

前面所讨论的极值问题,对于函数的自变量,除了限制它在定义域内之外,再无其它的约束条件,因此,我们称这类极值为无条件极值。

但是,在实际问题中,有时会遇到对函数的自变量还有附加限制条件的极值问题。

例如: 求体积为2而表面积最小的长方体尺寸。

若设长方体的长宽高分别为,则其表面积为

这里除了外,还需满足限制条件 。

象这类自变量有附加条件的极值称为条件极值。

有些实际问题,可将条件极值化为无条件极值,如上例；但对一些复杂的问题，条件极值很难化为无条件极值。因此,我们有必要探讨求条件极值的一般方法。

1、函数取得条件极值的必要条件

欲寻求函数                                     (1)

在限制条件                                         (2)

下的取得条件极值的条件。

函数若是在处取得条件极值,那么它必满足方程(2),即

                                   (3)

另外,方程(2)可确定一个隐函数,将之代入(1)有

                                  (4)

这样,函数(1)在取得条件极值,也就相当于函数(4)在处取得无条件极值。

据一元函数取得极值的必要条件有

             (5)

由(2)式有

代入到第(5)式有

                   (6)

由上面的讨论可知,(3)与(6)便是函数在点取得条件极值的必要条件,只是这一式子的形式不够工整,不便于记忆,为此,我们作适当的变形。

令  ，有

这三个式子恰好是函数

的三个偏导数在点的值。

2、拉格朗日乘数法

要求函数在限制条件下的可能极值点,可先作拉氏函数

再解方程组

求出点,这样求出的点就是可疑条件极值点。

【注记】拉氏乘数法可推广到一般元函数或限制条件多于一个的情形:

例如:求    在限制条件

下的极值。

作拉氏函数

解方程组

这样求出就是可疑极值点的坐标。