STL List::sort() 解析

转载地址：http://jiguiyuan.blog.163.com/blog/static/4336137820122133373886/

看侯捷翻译那本《STL源码剖析》中list内置sort的算法，书中注释说是quick sort，看了半天没看明白，

然后就把代码敲出来运行看看，上面的源码如下：

template

template

void list::sort()

{

if (node->next == node || link_type(node->next)->next == node)

return;

list carry;

list counter[64];

int fill = 0;

while (!empty())

{

carry.splice(carry.begin(), *this, begin());

int i = 0;

while (i < fill && !counter[i].empty())

{

counter[i].merge(carry);

carry.swap(counter[i++]);

}

carry.swap(counter[i]);

if (i == fill)

++fill;

}

for (int i = 1; i < fill; ++i)

counter[i].merge(counter[i - 1]);

swap(counter[fill - 1]);

}

对应的我的测试代码是：

typedef list IList;

void print(const IList& list)

{

IList::const_iterator ite = list.begin();

for (; ite != list.end(); ++ite)

{

cout << *ite << "  ";

}

cout << endl;

}

int main()

{

IList s;

s.push_back(7);

s.push_back(6);

s.push_back(5);

s.push_back(4);

s.push_back(3);

s.push_back(2);

s.push_back(1);

s.push_back(0);

IList carry;

IList counter[64];

int fill = 0;

int num = 0;

while (!s.empty())

{

cout << "取第" << num << "个数据: fill = " << fill << endl;

carry.splice(carry.begin(), s, s.begin());

int i = 0;

while (i < fill && !counter[i].empty())

{

counter[i].merge(carry);

carry.swap(counter[i++]);

}

carry.swap(counter[i]);

if (i == fill)

++fill;

//我自己加的计数

num++;

//打印每次完的结果

for (int i = 0; i < fill; ++i)

{

cout << i << "==";

print(counter[i]);

}

}

for (int i = 1; i < fill; ++i)

counter[i].merge(counter[i - 1]);

s.swap(counter[fill - 1]);

getchar();

return 0;

}

运行结果如下：

 

通过结果分析才发现明白这个算法是怎么回事，他是先归并前两个元素，然后归并后两个，再将这四个元素归并，

依次进行得到8个、16个……排好序的元素序列，在归并过程中counter数组里每个counter[i]中都存放的是2的

i次方个有序元素.其实这应该是一个归并排序，而不是注释所说的快速排序。

下面是别人对时间复杂度的分析：

假设总元素个数N=2^n-1。

首先merge函数的复杂度为O(m)，因此最后一步的for循环复杂度为 求和i:2~n{2^i-1}=O(N)的时间。

再看while循环，tmp[0]有1个元素，tmp[1]有2个元素，。。。，tmp[n-1]有2^(n-1)个元素，他们都是通过 merge而后再swap(为常数时间）到最终层次的，因此总复杂度为：求和i:1~n{i*2^(i-1)}=O((n- 1)*2^n)=O(N*lgN)。

因此总时间复杂度为N*lgN。

（ 时间复杂度分析源自http://hi.baidu.com/_%C2%B7_%C8%CB_%BC%D7_/blog/item/c7dfc017398ab11a5baf534e.html）

转载地址：http://hi.baidu.com/passerryan/item/7c0385356d48dc9fb90c0324

关于stl_list的sort算法

原文地址：http://www.blog.edu.cn/user1/5010/archives/2006/1166534.shtml

stl中的list被实现为环状的双向链表，设置一个“哨”node作为end( )。list没有使用标准sort算法，而是实现自身的sort，本质上是mergesort（侯捷解释的是错的），但是采用了一个特殊的形式：

普通的mergesort直接将待排序的序列一分为二，然后各自递归调用mergesort，再使用Merge算法用O(n)的时间将已排完序的两个子序列归并，从而总时间效率为n*lg(n)。(mergesort是很好的排序算法，绝对时间很小，n*lg(n)之前的系数也很小，但是在内存中的排序算法中并不常见，我想可能主要还是因为耗空间太多，也是O(n))

list_sort所使用的mergesort形式上大不一样：将前两个元素归并，再将后两个元素归并，归并这两个小子序列成为4个元素的有序子序列；重复这一过程，得到8个元素的有序子序列，16个的，32个的。。。，直到全部处理完。主要调用了swap和merge函数，而这些又依赖于内部实现的transfer函数(其时间代价为O(1))。该mergesort算法时间代价亦为n*lg(n)，计算起来比较复杂。list_sort中预留了64个temp_list，所以最多可以处理2^64-1个元素的序列，这应该足够了：）

为何list不使用普通的mergesort呢?这比较好理解，因为每次找到中间元素再一分为二的代价实在太大了，不适合list这种非RandomAccess的容器。

为何list不使用标准sort算法呢(标准sort要求RandomAccessIterator)？至少普通的quicksort我觉得应该是可以的，具体原因等查查标准算法实现再来说了。

下面把gcc4.02中list_sort的实现贴上：

template
    void
    list<_Tp, _Alloc>::
    sort()
    {
      // Do nothing if the list has length 0 or 1.
      if (this->_M_impl._M_node._M_next != &this->_M_impl._M_node
   && this->_M_impl._M_node._M_next->_M_next != &this->_M_impl._M_node)
      {
        list __carry;
        list __tmp[64];
        list * __fill = &__tmp[0];
        list * __counter;

        do
   {
     __carry.splice(__carry.begin(), *this, begin());

     for(__counter = &__tmp[0];
   __counter != __fill && !__counter->empty();
   ++__counter)
       {
   __counter->merge(__carry);
   __carry.swap(*__counter);
       }
     __carry.swap(*__counter);
     if (__counter == __fill)
       ++__fill;
   }
while ( !empty() );

        for (__counter = &__tmp[1]; __counter != __fill; ++__counter)
          __counter->merge(*(__counter - 1));
        swap( *(__fill - 1) );
      }
    }

对它的复杂度分析只能简单说说了，实际工作在草稿纸上完成：

假设总元素个数N=2^n-1。

首先merge函数的复杂度为O(m)，因此最后一步的for循环复杂度为 求和i:2~n{2^i-1}=O(N)的时间。

再看do_while循环，tmp[0]有1个元素，tmp[1]有2个元素，。。。，tmp[n-1]有2^(n-1)个元素，他们都是通过merge而后再swap(为常数时间）到最终层次的，因此总复杂度为：求和i:1~n{i*2^(i-1)}=O((n-1)*2^n)=O(N*lgN)。

因此总时间复杂度为N*lgN。

转载地址：http://hi.baidu.com/oxcjfhxwtsacjnr/item/76346b32ae4368c3392ffad3

SGI STL list::sort()—快速排序（非递归实现方式）

头头不在，看了点自己喜欢的东东 ：） 
遇下面的源码，简单扫了下，晕头转向～

// list 不能使用STL 算法 sort()，必须使用自己的 sort() member function，
// 因为STL算法sort() 只接受RamdonAccessIterator.
// 本函式采用 quick sort.
template
void list::sort() {
// 以下判断，如果是空白串行，或仅有一个元素，就不做任何动作。
if (node->next == node || link_type(node->next)->next == node) return;

// 一些新的 lists，做为中介数据存放区
list carry;
list counter[64];
int fill = 0;
while (!empty()) {
    carry.splice(carry.begin(), *this, begin()); //取出list中的一个数据，存入carry
    int i = 0;
    while(i < fill && !counter[i].empty()) {
      counter[i].merge(carry);                   //将carry中的数据，和 counter[i]链中原有数据合并
      carry.swap(counter[i++]);                  //交换carry 和counter[i] 数据
    }
    carry.swap(counter[i]);        
    if (i == fill) ++fill;
}

for (int i = 1; i < fill; ++i)                   // sort之后，善后处理，把数据统一起来
     counter[i].merge(counter[i-1]);
swap(counter[fill-1]);
}



你看出来了嘛？ 

详细道来：
fill ------> 2^fill 表示现在能处理的数据的最大数目
counter[ fill ]---> 将处理完的2^fill个数据存入 counter[ fill ]中
carry---> 就像一个临时中转站, 在处理的数据不足 2 ^ fil l时，在counter[ i ] ( 0=
步骤如下： 
1) 读入一个数据（carry.splice），通过 carry 将数据存入 counter[0] 中;
     随后处理下一个数据, carry 保存数据
            a. counter[0].merge(carry) , 此时 counter[0] 容纳的数据个数 > 2^0 
            b. 将counter[0]链中的数据，通过carry，转移到counter[1]链，.... 直至处理的数据个数达到 2 ^ fill 

2) fill++ , 重复 1) 至处理完所有的数据。


非递归的快速排序实现方式，很巧妙!!!
counter 数组为64 --- 所以此算法，一次最多能处理 2 ^ 64 -2 个数据 

转载地址：http://www.cnblogs.com/qlee/archive/2011/05/10/2042176.html

list::sort() 源码解释

Posted on  2011-05-10 15:18  李大嘴 阅读( 852) 评论( 0)  编辑  收藏

1 template < class T, class Alloc > 2 3   void list < T, Alloc > ::sort() { 4 5 if (node -> next == node || link_type(node -> next) -> next == node) return ; 6 7 list < T, Alloc > carry; 8 9 list < T, Alloc > counter[ 64 ]; 10 11 int fill = 0 ; 12 13 while ( ! empty()) { 14 15 carry.splice(carry.begin(), * this , begin()); 16 17 int i = 0 ; 18 19 while (i < fill && ! counter[i].empty()) { 20 21 counter[i].merge(carry); 22 23 carry.swap(counter[i ++ ]); 24 25 } 26 27 carry.swap(counter[i]); 28 29 if (i == fill) ++ fill; 30 31 } 32 33 for ( int i = 1 ; i < fill; ++ i) counter[i].merge(counter[i - 1 ]); 34 35 swap(counter[fill - 1 ]); 36 37 }

这是sgi stl的 list.sort源码

侯捷的STL源码剖析 有对很多源码进行了解释，但这个函数切只是翻译了下原注释几乎没有对核心进行解释，而且貌似他的解释还是错误的。他说此函数采用quick sort。但没有发现快速排序的特征，没有找基准的位置，没有划分为左右，也不是内部排序..等。

第6章的算法的泛化过程find例子 貌似也错了。find函数返回比较不应该用数组的end()来比较，而应当用find函数的第2个参数做比较！

/* Written     By     MaiK */

    STL中的list被实现为环状的双向链表，设置一个“哨兵”node作为end( )。鉴于list的内存分配模型,list不能使用通用的标准sort算法，而是实现自身的sort，但是list有自己的成员函数sort()可供其自身调用,其实际模型是基于合并排序的。普通的mergesort直接将待排序的序列一分为二，然后各自递归调用mergesort，再使用Merge算法用O(n)的时间将已排完序的两个子序列归并，从而总时间效率为n*lg(n)。(mergesort是很好的排序算法，绝对时间很小，n*lg(n)之前的系数也很小，但是在内存中的排序算法中并不常见，我想可能主要还是因为耗空间太多，也是O(n)).

    不过list_sort所使用的mergesort形式上大不一样：将前两个元素归并，再将后两个元素归并，归并这两个小子序列成为4个元素的有序子序列；重复这一过程，得到8个元素的有序子序列，16个的，32个的。。。，直到全部处理完。主要调用了swap和merge函数，而这些又依赖于内部实现的transfer函数(其时间代价为O(1))。该mergesort算法时间代价亦为n*lg(n)，计算起来比较复杂。list_sort中预留了 64个temp_list，所以最多可以处理2^64-1个元素的序列，这应该足够了。

/* Written     By    Lamar */

    类似2进制，每一次进位都是相邻高位数值的一半，所以是类2进制地。例如8，低位4满之后会进4个到8的。

转载地址：http://blog.chinaunix.net/uid-10647744-id-3083049.html 

SGI STL笔记（list中的sort算法）

STL的list容器提供了专有的sort算法，是一个以非递归形式的merge sort，虽然研究多时，无奈本人算法功底不济，本文权当抛砖引玉，望各路高手指点。

代码：

 template <class _Tp, class _Alloc>
 template <class _StrictWeakOrdering>
 void list<_Tp, _Alloc>::sort(_StrictWeakOrdering __comp)
 {
     // Do nothing if the list has length 0 or 1.
     if (_M_node->_M_next != _M_node && _M_node->_M_next->_M_next != _M_node) {
         // 保存下层merge返回的结果
         list<_Tp, _Alloc> __carry;
         // 模拟merge sort使用的堆栈，保存部分有序的list
         // 64应该写作sizeof(size_type) * 8，即最大的递归调用层次。
         list<_Tp, _Alloc> __counter[64];
         // 指示堆栈层次
         int __fill = 0;
         while (!empty()) {
             // 将begin处的元素从list取下，insert到carry中
             __carry.splice(__carry.begin(), *this, begin());
             int __i = 0;
             // 模拟递归时对下层的返回结果进行merge，并将结果交给carry
             while(__i < __fill && !__counter[__i].empty()) {
                 __counter[__i].merge(__carry, __comp);
                 __carry.swap(__counter[__i++]);
             }
             // carry将结果保存到堆栈
             __carry.swap(__counter[__i]);
             // 更新递归层次
             if (__i == __fill) ++__fill;
         }

         // 逐级获取结果
         for (int __i = 1; __i < __fill; ++__i)
             __counter[__i].merge(__counter[__i-1], __comp);
         // 保存最终结果
         swap(__counter[__fill-1]);
     }
 }

再免费赠送一个正常merge sort的C实现：）

 void merge(int *vector, size_t size)
 {
     // return if there's 0 or 1 element.
     if (size <= 1) {
         return ;
     }

     int half = size / 2;

     merge(vector, half);
     merge(vector + half, size - half);

     merge_aux(vector, size);

     return ;
 }

 static void merge_aux(int *vector, size_t size)
 {
     int i, j, k;

     int half = size / 2;

     int clone[half];

     for (i = 0; i < half; ++i) {
         clone[i] = vector[i];
     }

     for (i = 0, j = half, k = 0; (i < half) && (j < size); ++k) {
         if (clone[i] < vector[j]) {
             swap(vector[k], clone[i]);
             ++i;
         }
         else {
             swap(vector[k], vector[j]);
             ++j;
         }
     }

     while (i < half) {
         vector[k++] = clone[i++];
     }

     return ;
 }

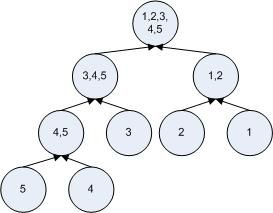
以下以对数据（5, 4, 3, 2, 1）排序为例，比较二者的主要差别。

1）递归形式：（圆圈内为本层排序好的数据）

图1

因为递归形式的merge sort在每一层都对数据进行分解，所以递归树是一棵完全二叉树。

2）非递归形式：

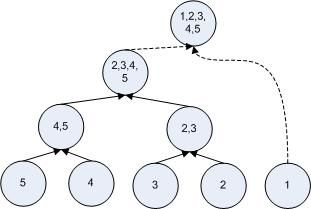
图2

因为非递归形式的算法是自底向上来merge数据，原始数据都处在同一层上，所以部分数据缺少中间的层次，最后仍然需要对这些结果再做一次合并（图2虚线引出的那些单元，就是由list::sort中最后那个for循环所处理）。

另外，由list本身来提供sort算法并不符合STL的设计原则，但若要将这样一个严重依赖底层实现的算法抽象出来，又需要做哪些改动呢？欢迎大家讨论。